苏科版数学九年级上册 4.2 第3课时 列表法 同步课件(共17张PPT)
文档属性
| 名称 | 苏科版数学九年级上册 4.2 第3课时 列表法 同步课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 369.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-13 11:24:08 | ||
图片预览





文档简介
(共17张PPT)
第4章 等可能条件下的概率
4.2 第3课时 列表法
知识回顾
当一次试验要涉及3个或更多的因素(例如抛掷一枚质地均匀的硬币3次)时,列表就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图.当事件要经过多次步骤(三步以上)完成时,用“树状图”的方法求事件的概率很有效.
(2021·长沙市)有一枚质地均匀的正方体骰子,六个面上分别刻有1到6的点数.将它投掷两次,则两次掷得骰子朝上一面的点数之和为5的概率是( )
A. B. C. D.
情景引入
通过树状图来列出抛掷两次骰子的所有等可能出现的结果:
骰子1
骰子2
开始
所有可能出现的结果共有:6×6=36种.
1点
2点
3点
4点
5点
6点
1点
2点
3点
4点
5点
6点
抛掷两枚骰子,点数之和是5的情况有4种,
树状图罗列篇幅过大,有没有更简便的方法呢?
可以用列表法.
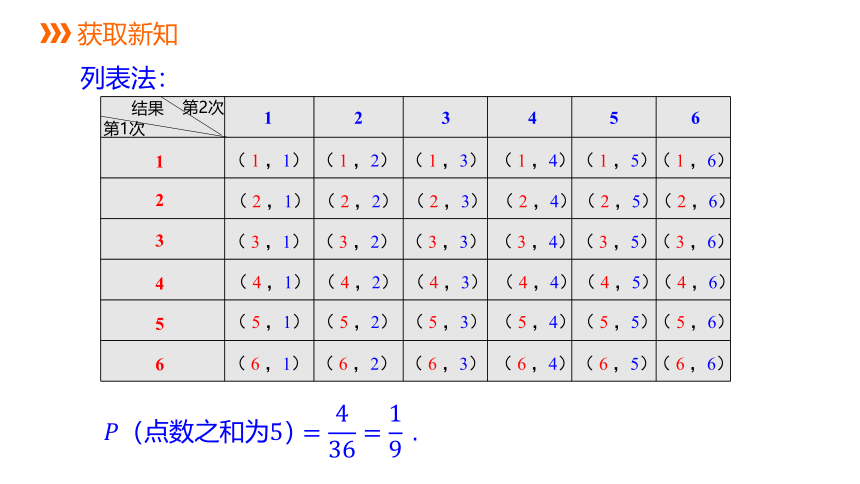
列表法:
第1次
第2次
结果
1
2
3
4
5
6
1
2
3
4
5
6
( 1 ,1)
( 1 ,2)
( 1 ,3)
( 1 ,4)
( 1 ,5)
( 1 ,6)
( 2 ,1)
( 2 ,2)
( 2 ,3)
( 2 ,4)
( 2 ,5)
( 2 ,6)
( 3 ,1)
( 3 ,2)
( 3 ,3)
( 3 ,4)
( 3 ,5)
( 3 ,6)
( 4 ,1)
( 4 ,2)
( 4 ,3)
( 4 ,4)
( 4 ,5)
( 4 ,6)
( 5 ,1)
( 5 ,2)
( 5 ,3)
( 5 ,4)
( 5 ,5)
( 5 ,6)
( 6 ,1)
( 6 ,2)
( 6 ,3)
( 6 ,4)
( 6 ,5)
( 6 ,6)
获取新知
当一次试验要涉及两个因素(例如掷两个骰子)并且可能出现的结果数目较多时,为不重不漏且清晰地列出所有可能的结果,通常采用列表法.
知识要点
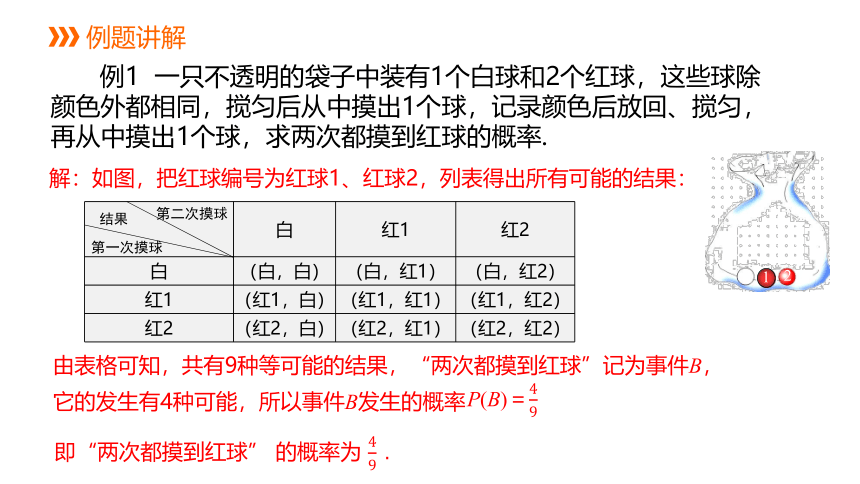
例1 一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中摸出1个球,记录颜色后放回、搅匀,再从中摸出1个球,求两次都摸到红球的概率.
例题讲解
解:如图,把红球编号为红球1、红球2,列表得出所有可能的结果:
1
2
白 红1 红2
白 (白,白) (白,红1) (白,红2)
红1 (红1,白) (红1,红1) (红1,红2)
红2 (红2,白) (红2,红1) (红2,红2)
第二次摸球
第一次摸球
结果
由表格可知,共有9种等可能的结果,“两次都摸到红球”记为事件B,
它的发生有4种可能,所以事件B发生的概率
即“两次都摸到红球” 的概率为
P(B)=
变式 一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中摸出1个球,记录颜色后不放回,再从中摸出1个球,求两次都摸到红球的概率.
解:如图,把红球编号为红球1、红球2,列表得出所有可能的结果:
1
2
白 红1 红2
白 (白,红1) (白,红2)
红1 (红1,白) (红1,红2)
红2 (红2,白) (红2,红1)
第二次摸球
第一次摸球
结果
第1次摸出的球不放回,两次都摸到红球的概率为
例2. 北京2008年奥运会吉祥物“福娃”是“贝贝、晶晶、欢欢、迎迎、妮妮”:
将5张分别印有5个“福娃”图案的卡片(卡片的形状、大小、质地都相同)放在盒子中,搅匀后从中任意取出1张卡片,记录后放回、搅匀,再从中任意取出1张卡片.求下列事件的发生的概率:
(1)取出的2张卡片图案相同;
(2)取出的2张卡片中,1张为“欢欢”,1张为“贝贝”;
(3)取出的2张卡片中,至少有1张为“欢欢”.
解: 将印有“贝贝、晶晶、欢欢、迎迎、妮妮”的卡片分别编号为1、2、3、4、5,用表格列出所有可能的结果:
1 2 3 4 5
1 (1,1) (1,2) (1,3) (1,4) (1,5)
2 (2,1) (2,2) (2,3) (2,4) (2,5)
3 (3,1) (3,2) (3,3) (3,4) (3,5)
4 (4,1) (4,2) (4,3) (4,4) (4,5)
5 (5,1) (5,2) (5,3) (5,4) (5,5)
第二次
取出
卡片
第一次
取出卡片
结果
由表格可知,共有25种可能的结果,并且它们的出现是等可能的.
(1)“取出的2张卡片图案相同”记为事件A,它的发生有5种可能,即(1,1),(2,2),(3,3),(4,4),(5,5),所以事件A发生的概率为
(2)“取出的2张卡片中,1张为欢欢,1张为贝贝”记为事件B,它的发生有2种可能,即(1,3),(3,1),所以事件B发生的概率为
P(A)
P(B)
(3)“取出的2张卡片中,至少有1张为欢欢”记为事件C,它的发生有9种可能,即(1,3),(2,3),(3,3),(4,3),(5,3),(3,1),(3,2),(3,4),(3,5),所以事件C发生的概率为
P(C)
当一次试验涉及两个因素,并且可能出现的结果数目较多时,为不重不漏地列出所有可能的结果,通常采用列表法. 列表时要注意“放回”与“不放回”的区别.
归纳总结
当一次试验要涉及3个或更多的因素(例如抛掷一枚质地均匀的硬币3次)时,列表就不方便了,为了不重不漏地列出所有可能的结果,通常采用树形图.当事件要经过多次步骤(三步以上)完成时,用这种“树状图”的方法求事件的概率很有效.
随堂演练
1.小明与小红玩一次“石头、剪刀、布”游戏,则小明赢的概率是( )
B
A. B. C. D.
2.(2021·重庆)不透明袋子中装有黑球1个、白球2个,这些球除了颜色外无其他差别.从袋子中随机摸出一个球,记下颜色后放回,将袋子中的球摇匀,再随机摸出一个球,记下颜色,前后两次摸出的球都是白球的概率是__________.
3.(2021·陕西)从一副普通的扑克牌中取出四张牌,它们的牌面数字分别为2,3,3,6.
(1)将这四张扑克牌背面朝上,洗匀,从中随机抽取一张,则抽取的这张牌的牌面数字是3的概率为_________;
(2)将这四张扑克牌背面朝上,洗匀.从中随机抽取一张,不放回,再从剩余的三张牌中随机抽取一张.请利用画树状图或列表的方法,求抽取的这两张牌的面数字恰好相同的概率.
(2)解:列表如下:
2 3 3 6
2
3
3
6
第二次
第一次
结果
(2,3)
(2,3)
(2,6)
(3,2)
(3,3)
(3,6)
(3,2)
(3,3)
(3,6)
(6,2)
(6,3)
(6,3)
由上表可知,共有12种等可能的结果,其中牌面数字恰好相同的结果有2种,
P(牌面数字相同) .
课堂小结
用列表法求概率
步骤
适用对象
两个试验因素或分两步进行的试验.
③代入概率公式进行计算.
①列表呈现出所有可能的结果;
②统计出m和n的值;
前提条件
确保试验中每种结果出现的可能性大小相等.
第4章 等可能条件下的概率
4.2 第3课时 列表法
知识回顾
当一次试验要涉及3个或更多的因素(例如抛掷一枚质地均匀的硬币3次)时,列表就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图.当事件要经过多次步骤(三步以上)完成时,用“树状图”的方法求事件的概率很有效.
(2021·长沙市)有一枚质地均匀的正方体骰子,六个面上分别刻有1到6的点数.将它投掷两次,则两次掷得骰子朝上一面的点数之和为5的概率是( )
A. B. C. D.
情景引入
通过树状图来列出抛掷两次骰子的所有等可能出现的结果:
骰子1
骰子2
开始
所有可能出现的结果共有:6×6=36种.
1点
2点
3点
4点
5点
6点
1点
2点
3点
4点
5点
6点
抛掷两枚骰子,点数之和是5的情况有4种,
树状图罗列篇幅过大,有没有更简便的方法呢?
可以用列表法.
列表法:
第1次
第2次
结果
1
2
3
4
5
6
1
2
3
4
5
6
( 1 ,1)
( 1 ,2)
( 1 ,3)
( 1 ,4)
( 1 ,5)
( 1 ,6)
( 2 ,1)
( 2 ,2)
( 2 ,3)
( 2 ,4)
( 2 ,5)
( 2 ,6)
( 3 ,1)
( 3 ,2)
( 3 ,3)
( 3 ,4)
( 3 ,5)
( 3 ,6)
( 4 ,1)
( 4 ,2)
( 4 ,3)
( 4 ,4)
( 4 ,5)
( 4 ,6)
( 5 ,1)
( 5 ,2)
( 5 ,3)
( 5 ,4)
( 5 ,5)
( 5 ,6)
( 6 ,1)
( 6 ,2)
( 6 ,3)
( 6 ,4)
( 6 ,5)
( 6 ,6)
获取新知
当一次试验要涉及两个因素(例如掷两个骰子)并且可能出现的结果数目较多时,为不重不漏且清晰地列出所有可能的结果,通常采用列表法.
知识要点
例1 一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中摸出1个球,记录颜色后放回、搅匀,再从中摸出1个球,求两次都摸到红球的概率.
例题讲解
解:如图,把红球编号为红球1、红球2,列表得出所有可能的结果:
1
2
白 红1 红2
白 (白,白) (白,红1) (白,红2)
红1 (红1,白) (红1,红1) (红1,红2)
红2 (红2,白) (红2,红1) (红2,红2)
第二次摸球
第一次摸球
结果
由表格可知,共有9种等可能的结果,“两次都摸到红球”记为事件B,
它的发生有4种可能,所以事件B发生的概率
即“两次都摸到红球” 的概率为
P(B)=
变式 一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中摸出1个球,记录颜色后不放回,再从中摸出1个球,求两次都摸到红球的概率.
解:如图,把红球编号为红球1、红球2,列表得出所有可能的结果:
1
2
白 红1 红2
白 (白,红1) (白,红2)
红1 (红1,白) (红1,红2)
红2 (红2,白) (红2,红1)
第二次摸球
第一次摸球
结果
第1次摸出的球不放回,两次都摸到红球的概率为
例2. 北京2008年奥运会吉祥物“福娃”是“贝贝、晶晶、欢欢、迎迎、妮妮”:
将5张分别印有5个“福娃”图案的卡片(卡片的形状、大小、质地都相同)放在盒子中,搅匀后从中任意取出1张卡片,记录后放回、搅匀,再从中任意取出1张卡片.求下列事件的发生的概率:
(1)取出的2张卡片图案相同;
(2)取出的2张卡片中,1张为“欢欢”,1张为“贝贝”;
(3)取出的2张卡片中,至少有1张为“欢欢”.
解: 将印有“贝贝、晶晶、欢欢、迎迎、妮妮”的卡片分别编号为1、2、3、4、5,用表格列出所有可能的结果:
1 2 3 4 5
1 (1,1) (1,2) (1,3) (1,4) (1,5)
2 (2,1) (2,2) (2,3) (2,4) (2,5)
3 (3,1) (3,2) (3,3) (3,4) (3,5)
4 (4,1) (4,2) (4,3) (4,4) (4,5)
5 (5,1) (5,2) (5,3) (5,4) (5,5)
第二次
取出
卡片
第一次
取出卡片
结果
由表格可知,共有25种可能的结果,并且它们的出现是等可能的.
(1)“取出的2张卡片图案相同”记为事件A,它的发生有5种可能,即(1,1),(2,2),(3,3),(4,4),(5,5),所以事件A发生的概率为
(2)“取出的2张卡片中,1张为欢欢,1张为贝贝”记为事件B,它的发生有2种可能,即(1,3),(3,1),所以事件B发生的概率为
P(A)
P(B)
(3)“取出的2张卡片中,至少有1张为欢欢”记为事件C,它的发生有9种可能,即(1,3),(2,3),(3,3),(4,3),(5,3),(3,1),(3,2),(3,4),(3,5),所以事件C发生的概率为
P(C)
当一次试验涉及两个因素,并且可能出现的结果数目较多时,为不重不漏地列出所有可能的结果,通常采用列表法. 列表时要注意“放回”与“不放回”的区别.
归纳总结
当一次试验要涉及3个或更多的因素(例如抛掷一枚质地均匀的硬币3次)时,列表就不方便了,为了不重不漏地列出所有可能的结果,通常采用树形图.当事件要经过多次步骤(三步以上)完成时,用这种“树状图”的方法求事件的概率很有效.
随堂演练
1.小明与小红玩一次“石头、剪刀、布”游戏,则小明赢的概率是( )
B
A. B. C. D.
2.(2021·重庆)不透明袋子中装有黑球1个、白球2个,这些球除了颜色外无其他差别.从袋子中随机摸出一个球,记下颜色后放回,将袋子中的球摇匀,再随机摸出一个球,记下颜色,前后两次摸出的球都是白球的概率是__________.
3.(2021·陕西)从一副普通的扑克牌中取出四张牌,它们的牌面数字分别为2,3,3,6.
(1)将这四张扑克牌背面朝上,洗匀,从中随机抽取一张,则抽取的这张牌的牌面数字是3的概率为_________;
(2)将这四张扑克牌背面朝上,洗匀.从中随机抽取一张,不放回,再从剩余的三张牌中随机抽取一张.请利用画树状图或列表的方法,求抽取的这两张牌的面数字恰好相同的概率.
(2)解:列表如下:
2 3 3 6
2
3
3
6
第二次
第一次
结果
(2,3)
(2,3)
(2,6)
(3,2)
(3,3)
(3,6)
(3,2)
(3,3)
(3,6)
(6,2)
(6,3)
(6,3)
由上表可知,共有12种等可能的结果,其中牌面数字恰好相同的结果有2种,
P(牌面数字相同) .
课堂小结
用列表法求概率
步骤
适用对象
两个试验因素或分两步进行的试验.
③代入概率公式进行计算.
①列表呈现出所有可能的结果;
②统计出m和n的值;
前提条件
确保试验中每种结果出现的可能性大小相等.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
