人教版七年级数学上册1.2.4绝对值课件(共17张PPT)
文档属性
| 名称 | 人教版七年级数学上册1.2.4绝对值课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-13 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
第一章 有理数
1.2.2 绝对值
1,什么是数轴?数轴的三要素是什么?
知识回顾
数轴是规定了原点,正方向,单位长度的一条直线
2,什么是相反数?
只有符号不同的两个数叫做互为相反数
规定:0的相反数是0.
1,理解绝对值的概念及性质.(难点、重点)
学习目标
2,会求一个有理数的绝对值.
3,能对绝对值进行计算.
两辆汽车从同一处O出发,分别向东,向西方向行
驶10km,到达A,B两处,它们行驶的路线相同吗?
它们的行驶路程相等吗?
新课导入
-10
10
0
O
B
A
结论:它们的行驶路线不同,行驶路程相同
规定向东行驶为正方向,甲乙两车分别从O点出发
甲车向东行驶10km到达A处,记作
乙车向西行驶10km到达B处,记作
合作探究
-10
10
0
O
B
A
结论:它们的行驶路线不同,行驶路程相同
+10km
-10km
10
10
追问:画一条数轴,在数轴上表示-3的点到原点的
距离是多少?表示3的点呢?表示2.5和-2.5呢?
合作探究
结论:在数轴上,表示-3和3的点到原点的距离都是3
在数轴上,表示-2.5和2.5的点到原点的距离都
是2.5
-1
-4
-3
-2
0
1
2
3
4
-6
-5
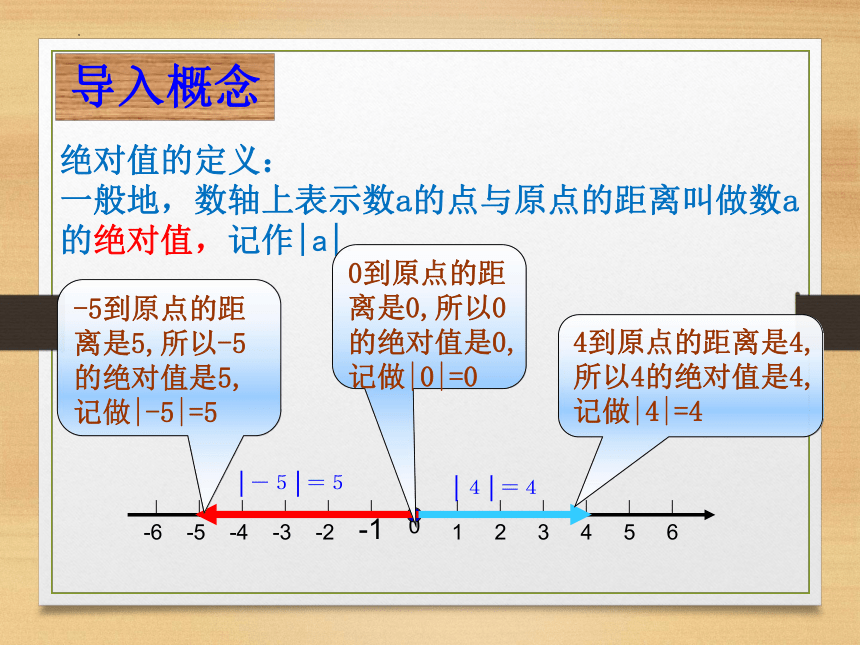
绝对值的定义:
一般地,数轴上表示数a的点与原点的距离叫做数a
的绝对值,记作|a|.
导入概念
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
│-5│=5
│4│=4
-5到原点的距离是5,所以-5的绝对值是5,记做|-5|=5
0到原点的距离是0,所以0的绝对值是0,记做|0|=0
4到原点的距离是4,所以4的绝对值是4,记做|4|=4
结合数轴快速回答数轴上点到原点的距离
|4|=
|2.5|=
|-3|=
|-3.5|=
|0|=
0
1
0
0
0
0
4
2.5
-3
-3.5
4
2.5
3
3.5
0
合作讨论
1.-5的绝对值是 ,说明数轴上表示-2的点到 的距
离是 个单位长度。
合作讨论
5
原点
5
2,-0.9的绝对值是 ,1.5的绝对值是
0.9
3,到原点距离为3个单位的点表示的数是
3和-3
4,绝对值等于0的数是___,
0
1.5
思考
一个正数的绝对值是什么?
一个负数的绝对值是什么?
0的绝对值是什么?
结论
由绝对值的定义可知:
一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.
即:(1)当a>0时,|a|=____;
(2)当a<0时,|a|=__;
(3)当a=0时,|a|=___.
正数的绝对值是它本身
a
负数的绝对值是它的相反数
-a
0的绝对值是0
0
数学语言
合作讨论
即对于任意有理数都有,
1,有没有绝对值等于-3的数?
|a|≥0
归纳总结
无论有理数a取何值,它的绝对值总
是正数或者0
2,一个数的绝对值会是负数吗?为什么?
3,无论有理数a取何值,它的绝对值总是什么数?
互为相反数的两个数的绝对值有什么关系?
合作讨论
|+3|=3
|+3|=3
绝对值相等
互为相反数,符号相反
互为相反数的两个数的绝对值相等.
绝对值相等,符号相反的两个数互为相反数.
判断下列说法是否正确
课堂小练
1,符号相反的数互为相反数
×
2一个数的绝对值越大,表示它的点在数轴上越靠右
4,当a≠0时,|a|总是大于0.
3,一个数的绝对值越大,表示它的点在数轴上离原点越远。
×
√
√
5,有理数的绝对值一定是正数.
6,若|a|=|b|,则a=b.
×
×
7,若a=-b,则|a|=|b|.
8,若|a|=-a,则a必为负数.
√
×
判断下列说法是否正确
课堂小练
1,一个数的绝对值等于本身,则这个数一定是正数
×
2一个数的绝对值等于它的相反数,这个数一定是负数
×
3,如果两个数不相等,那么这两个数的绝对值
一定不等.
4,如果两个数的绝对值相等,那么这两个数一定
相等;
×
×
1,求下列各数的绝对值
课堂小练
2,绝对值等于9的数是_______.
3,到原点距离是4个单位的点表示的数是 .
11, -2.5, 0.
易错提醒: 注意绝对值等于某个正数的数有两个,他们互为相反数,解题时不要遗漏负值.
课堂小练
解:根据题意可知
x-4=0,y-3=0,
所以x=4,y=3,故x+y=7.
归纳总结: 几个非负数的和为0,则这几个数都为0.
课堂小结
1,数轴上表示数a的点与原点的距离叫做a的绝对值。
记作|a|.
2,绝对值的性质一:非负性 |a|≥0
性质二:
第一章 有理数
1.2.2 绝对值
1,什么是数轴?数轴的三要素是什么?
知识回顾
数轴是规定了原点,正方向,单位长度的一条直线
2,什么是相反数?
只有符号不同的两个数叫做互为相反数
规定:0的相反数是0.
1,理解绝对值的概念及性质.(难点、重点)
学习目标
2,会求一个有理数的绝对值.
3,能对绝对值进行计算.
两辆汽车从同一处O出发,分别向东,向西方向行
驶10km,到达A,B两处,它们行驶的路线相同吗?
它们的行驶路程相等吗?
新课导入
-10
10
0
O
B
A
结论:它们的行驶路线不同,行驶路程相同
规定向东行驶为正方向,甲乙两车分别从O点出发
甲车向东行驶10km到达A处,记作
乙车向西行驶10km到达B处,记作
合作探究
-10
10
0
O
B
A
结论:它们的行驶路线不同,行驶路程相同
+10km
-10km
10
10
追问:画一条数轴,在数轴上表示-3的点到原点的
距离是多少?表示3的点呢?表示2.5和-2.5呢?
合作探究
结论:在数轴上,表示-3和3的点到原点的距离都是3
在数轴上,表示-2.5和2.5的点到原点的距离都
是2.5
-1
-4
-3
-2
0
1
2
3
4
-6
-5
绝对值的定义:
一般地,数轴上表示数a的点与原点的距离叫做数a
的绝对值,记作|a|.
导入概念
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
│-5│=5
│4│=4
-5到原点的距离是5,所以-5的绝对值是5,记做|-5|=5
0到原点的距离是0,所以0的绝对值是0,记做|0|=0
4到原点的距离是4,所以4的绝对值是4,记做|4|=4
结合数轴快速回答数轴上点到原点的距离
|4|=
|2.5|=
|-3|=
|-3.5|=
|0|=
0
1
0
0
0
0
4
2.5
-3
-3.5
4
2.5
3
3.5
0
合作讨论
1.-5的绝对值是 ,说明数轴上表示-2的点到 的距
离是 个单位长度。
合作讨论
5
原点
5
2,-0.9的绝对值是 ,1.5的绝对值是
0.9
3,到原点距离为3个单位的点表示的数是
3和-3
4,绝对值等于0的数是___,
0
1.5
思考
一个正数的绝对值是什么?
一个负数的绝对值是什么?
0的绝对值是什么?
结论
由绝对值的定义可知:
一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.
即:(1)当a>0时,|a|=____;
(2)当a<0时,|a|=__;
(3)当a=0时,|a|=___.
正数的绝对值是它本身
a
负数的绝对值是它的相反数
-a
0的绝对值是0
0
数学语言
合作讨论
即对于任意有理数都有,
1,有没有绝对值等于-3的数?
|a|≥0
归纳总结
无论有理数a取何值,它的绝对值总
是正数或者0
2,一个数的绝对值会是负数吗?为什么?
3,无论有理数a取何值,它的绝对值总是什么数?
互为相反数的两个数的绝对值有什么关系?
合作讨论
|+3|=3
|+3|=3
绝对值相等
互为相反数,符号相反
互为相反数的两个数的绝对值相等.
绝对值相等,符号相反的两个数互为相反数.
判断下列说法是否正确
课堂小练
1,符号相反的数互为相反数
×
2一个数的绝对值越大,表示它的点在数轴上越靠右
4,当a≠0时,|a|总是大于0.
3,一个数的绝对值越大,表示它的点在数轴上离原点越远。
×
√
√
5,有理数的绝对值一定是正数.
6,若|a|=|b|,则a=b.
×
×
7,若a=-b,则|a|=|b|.
8,若|a|=-a,则a必为负数.
√
×
判断下列说法是否正确
课堂小练
1,一个数的绝对值等于本身,则这个数一定是正数
×
2一个数的绝对值等于它的相反数,这个数一定是负数
×
3,如果两个数不相等,那么这两个数的绝对值
一定不等.
4,如果两个数的绝对值相等,那么这两个数一定
相等;
×
×
1,求下列各数的绝对值
课堂小练
2,绝对值等于9的数是_______.
3,到原点距离是4个单位的点表示的数是 .
11, -2.5, 0.
易错提醒: 注意绝对值等于某个正数的数有两个,他们互为相反数,解题时不要遗漏负值.
课堂小练
解:根据题意可知
x-4=0,y-3=0,
所以x=4,y=3,故x+y=7.
归纳总结: 几个非负数的和为0,则这几个数都为0.
课堂小结
1,数轴上表示数a的点与原点的距离叫做a的绝对值。
记作|a|.
2,绝对值的性质一:非负性 |a|≥0
性质二:
