6.2.3平行四边形的判定课件北师大版八年级数学下册(共15张PPT)
文档属性
| 名称 | 6.2.3平行四边形的判定课件北师大版八年级数学下册(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 609.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-13 10:33:04 | ||
图片预览




文档简介
(共15张PPT)
6.2平行四边形的判定(3)
课题
一:回顾
1.平行四边形有哪些性质?
平行四边形的对边平行且相等.
平行四边形的对角相等.
平行四边形的对角线互相平分.
平行四边形
边
角
对角线
对称性
平行四边形具有中心对称性.
一:回顾
2.平行四边形的判定方法有哪些?
两组对边分别平行的四边形
两组对边分别相等的四边形
一组对边平行且相等的四边形
平行四边形
边
对角线
两条对角线互相平分的四边形
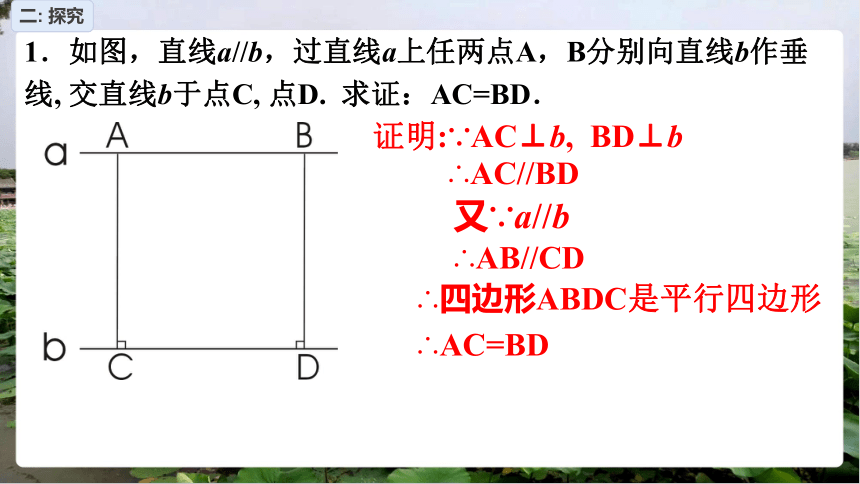
1.如图,直线a//b,过直线a上任两点A,B分别向直线b作垂线, 交直线b于点C, 点D. 求证:AC=BD.
二: 探究
证明:∵AC⊥b, BD⊥b
∴AC//BD
又∵a//b
∴AB//CD
∴四边形ABDC是平行四边形
∴AC=BD
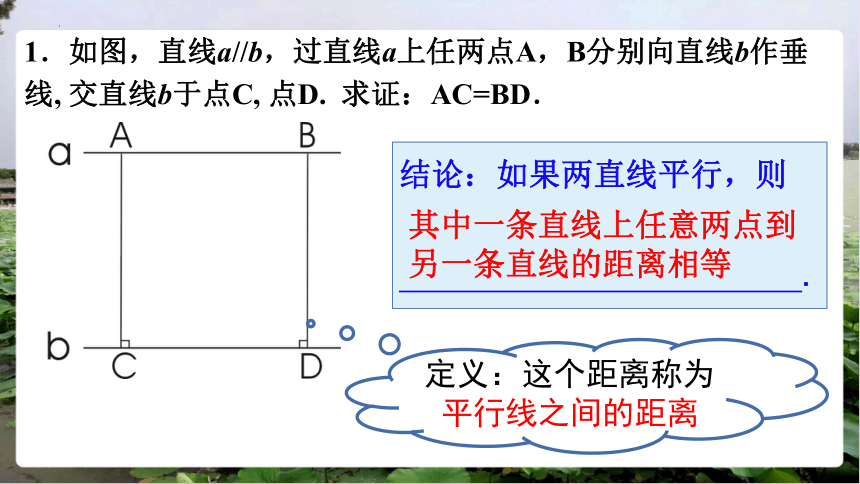
1.如图,直线a//b,过直线a上任两点A,B分别向直线b作垂线, 交直线b于点C, 点D. 求证:AC=BD.
结论:如果两直线平行,则
.
其中一条直线上任意两点到另一条直线的距离相等
定义:这个距离称为
平行线之间的距离
2.应用:如图,在□ABCD中,AB=AD,AE⊥BC,AF⊥CD。(1) 求证:AE=AF.(2)若AB=6,∠ABC=45°,求□ABCD的面积.
(1)证明:∵AE⊥BC, AF⊥CD
∵□ABCD
在△AEB和△AFD中
∠1=∠2
∠B=∠D
AB=AD
∴△AEB≌△AFD(AAS)
∴AE=AF
∴∠AEB=∠AFD=90°
∴∠B=∠D
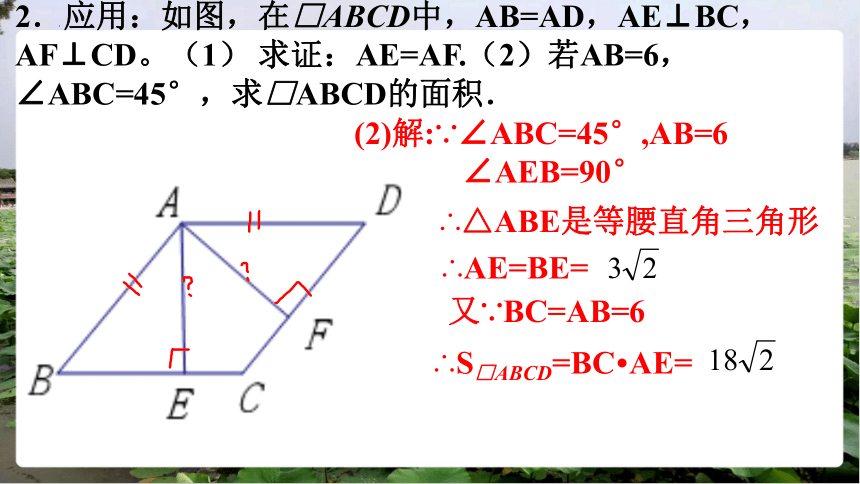
2.应用:如图,在□ABCD中,AB=AD,AE⊥BC,AF⊥CD。(1) 求证:AE=AF.(2)若AB=6,∠ABC=45°,求□ABCD的面积.
(2)解:∵∠ABC=45°,AB=6
∠AEB=90°
∴△ABE是等腰直角三角形
∴AE=BE=
又∵BC=AB=6
∴S□ABCD=BC AE=
三.反馈练习
1.已知四边形ABCD,有以下四个条件:①AB//CD;②AB=CD;③BC//AD;④BC=AD.从这四个条件中任选两个,能使四边形 ABCD成为平行四边形的选法种数共有( )
(A)6种 (B)5种 (C)4种 (D)3种
C
四.反馈练习
2.如图,在□ABCD 中,对角线 AC、BD 相交于点 O,若AC=14,BD=8,AB=10,则△OAB的周长为 .
21
四.反馈练习
3.如图,在□ABCD中,DE⊥AC,BF⊥AC,E,F是垂足.求证:四边形DEBF是平行四边形.
证明:∵DE⊥AC, BF⊥AC
∵□ABCD
在△AED和△CFB中
∠1=∠2
∠DAE=∠BCF
AD=BC
∴△AED≌△CFB(AAS)
∴DE//BF,
∠1=∠2=90°
∴AD=BC,
AD//BC,
∴∠DAE=∠BCF
∴DE=BF
∴四边形DEBF是平行四边形
四.反馈练习
4.如图,在□ABCD中,点M,N分别在AD和BC上,点E,F在BD上,且DM=BN,DF=BE.求证:四边形MENF是平行四边形.
证明:∵□ABCD
在△DMF和△BNE中
∠1=∠2
DM=BN
DF=BE
∴△DMF≌△BNE(SAS)
∴MF=NE,
∴AD//BC
∴∠1=∠2
∠MFD=∠BEN
∴∠MFE=∠FEN
∴MF//NE,
∴四边形MENF是平行四边形
四.反馈练习
5. 如图,在□ABCD 中,DE,BF 分别是∠ADC和∠ABC的平分线,交AB,CD于点E,F,连接BD,EF.求证:BD,EF互相平分.
证明:∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB,AD=BC.
又∵DE、BF平分∠ADC和∠ABC
∴∠ADE=∠CDE=∠AED
∠CBF=∠ABF=∠CFB
∴AE=AD,CF=CB,∴AE=CF,
∴AB-AE=CD-CF,即BE=DF.
∵DF∥BE,
∴四边形DEBF是平行四边形,
∴BD、EF互相平分.
三.反馈练习
6.如图所示,在□ABCD 中,E,F 分别在 BC,AD上,若想使四边形 AFCE 为平行四边形,须添加一个条件,这个条件可以是( )
①AF = CF; ②AE = CF;
③∠BAE = ∠FCD; ④∠BEA = ∠FCE.
A. ①或②
B. ②或③
C. ③或④
D. ①或③或④
C
三.反馈练习
7. 如图,四边形 ABCD 的对角线AC⊥BD,垂足为点 E,AB=BC,点F为四边形ABCD 外一点,且∠FCA=90°,∠CBF= ∠DCB.
(1)求证:四边形 DBFC 是平行四边形;
(2)如果BC平分∠DBF, ∠F=45°, BD=2,求 AC 的长.
(1)证明:
∵AC⊥BD, ∠FCA=90°,
∠CBF=∠DCB.
∴BD∥CF,CD∥BF,
∴四边形DBFC是平行四边形;
三.反馈练习
7. 如图,四边形 ABCD 的对角线AC⊥BD,垂足为点 E,AB=BC,点F为四边形ABCD 外一点,且∠FCA=90°,∠CBF= ∠DCB.
(1)求证:四边形 DBFC 是平行四边形;
(2)如果BC平分∠DBF, ∠F=45°, BD=2,求 AC 的长.
(2)解:∵□DBFC,∴CF=BD=2,
∵AB=BC,AC⊥BD,∴AE=CE,
作CM⊥BF,垂足为点M,
∵BC平分∠DBF,∴CE=CM,
∵∠F=45°,∴△CFM是等腰直角三角形,
∴CM= ,∴AE=CE= ,
∴AC=2 .
6.2平行四边形的判定(3)
课题
一:回顾
1.平行四边形有哪些性质?
平行四边形的对边平行且相等.
平行四边形的对角相等.
平行四边形的对角线互相平分.
平行四边形
边
角
对角线
对称性
平行四边形具有中心对称性.
一:回顾
2.平行四边形的判定方法有哪些?
两组对边分别平行的四边形
两组对边分别相等的四边形
一组对边平行且相等的四边形
平行四边形
边
对角线
两条对角线互相平分的四边形
1.如图,直线a//b,过直线a上任两点A,B分别向直线b作垂线, 交直线b于点C, 点D. 求证:AC=BD.
二: 探究
证明:∵AC⊥b, BD⊥b
∴AC//BD
又∵a//b
∴AB//CD
∴四边形ABDC是平行四边形
∴AC=BD
1.如图,直线a//b,过直线a上任两点A,B分别向直线b作垂线, 交直线b于点C, 点D. 求证:AC=BD.
结论:如果两直线平行,则
.
其中一条直线上任意两点到另一条直线的距离相等
定义:这个距离称为
平行线之间的距离
2.应用:如图,在□ABCD中,AB=AD,AE⊥BC,AF⊥CD。(1) 求证:AE=AF.(2)若AB=6,∠ABC=45°,求□ABCD的面积.
(1)证明:∵AE⊥BC, AF⊥CD
∵□ABCD
在△AEB和△AFD中
∠1=∠2
∠B=∠D
AB=AD
∴△AEB≌△AFD(AAS)
∴AE=AF
∴∠AEB=∠AFD=90°
∴∠B=∠D
2.应用:如图,在□ABCD中,AB=AD,AE⊥BC,AF⊥CD。(1) 求证:AE=AF.(2)若AB=6,∠ABC=45°,求□ABCD的面积.
(2)解:∵∠ABC=45°,AB=6
∠AEB=90°
∴△ABE是等腰直角三角形
∴AE=BE=
又∵BC=AB=6
∴S□ABCD=BC AE=
三.反馈练习
1.已知四边形ABCD,有以下四个条件:①AB//CD;②AB=CD;③BC//AD;④BC=AD.从这四个条件中任选两个,能使四边形 ABCD成为平行四边形的选法种数共有( )
(A)6种 (B)5种 (C)4种 (D)3种
C
四.反馈练习
2.如图,在□ABCD 中,对角线 AC、BD 相交于点 O,若AC=14,BD=8,AB=10,则△OAB的周长为 .
21
四.反馈练习
3.如图,在□ABCD中,DE⊥AC,BF⊥AC,E,F是垂足.求证:四边形DEBF是平行四边形.
证明:∵DE⊥AC, BF⊥AC
∵□ABCD
在△AED和△CFB中
∠1=∠2
∠DAE=∠BCF
AD=BC
∴△AED≌△CFB(AAS)
∴DE//BF,
∠1=∠2=90°
∴AD=BC,
AD//BC,
∴∠DAE=∠BCF
∴DE=BF
∴四边形DEBF是平行四边形
四.反馈练习
4.如图,在□ABCD中,点M,N分别在AD和BC上,点E,F在BD上,且DM=BN,DF=BE.求证:四边形MENF是平行四边形.
证明:∵□ABCD
在△DMF和△BNE中
∠1=∠2
DM=BN
DF=BE
∴△DMF≌△BNE(SAS)
∴MF=NE,
∴AD//BC
∴∠1=∠2
∠MFD=∠BEN
∴∠MFE=∠FEN
∴MF//NE,
∴四边形MENF是平行四边形
四.反馈练习
5. 如图,在□ABCD 中,DE,BF 分别是∠ADC和∠ABC的平分线,交AB,CD于点E,F,连接BD,EF.求证:BD,EF互相平分.
证明:∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB,AD=BC.
又∵DE、BF平分∠ADC和∠ABC
∴∠ADE=∠CDE=∠AED
∠CBF=∠ABF=∠CFB
∴AE=AD,CF=CB,∴AE=CF,
∴AB-AE=CD-CF,即BE=DF.
∵DF∥BE,
∴四边形DEBF是平行四边形,
∴BD、EF互相平分.
三.反馈练习
6.如图所示,在□ABCD 中,E,F 分别在 BC,AD上,若想使四边形 AFCE 为平行四边形,须添加一个条件,这个条件可以是( )
①AF = CF; ②AE = CF;
③∠BAE = ∠FCD; ④∠BEA = ∠FCE.
A. ①或②
B. ②或③
C. ③或④
D. ①或③或④
C
三.反馈练习
7. 如图,四边形 ABCD 的对角线AC⊥BD,垂足为点 E,AB=BC,点F为四边形ABCD 外一点,且∠FCA=90°,∠CBF= ∠DCB.
(1)求证:四边形 DBFC 是平行四边形;
(2)如果BC平分∠DBF, ∠F=45°, BD=2,求 AC 的长.
(1)证明:
∵AC⊥BD, ∠FCA=90°,
∠CBF=∠DCB.
∴BD∥CF,CD∥BF,
∴四边形DBFC是平行四边形;
三.反馈练习
7. 如图,四边形 ABCD 的对角线AC⊥BD,垂足为点 E,AB=BC,点F为四边形ABCD 外一点,且∠FCA=90°,∠CBF= ∠DCB.
(1)求证:四边形 DBFC 是平行四边形;
(2)如果BC平分∠DBF, ∠F=45°, BD=2,求 AC 的长.
(2)解:∵□DBFC,∴CF=BD=2,
∵AB=BC,AC⊥BD,∴AE=CE,
作CM⊥BF,垂足为点M,
∵BC平分∠DBF,∴CE=CM,
∵∠F=45°,∴△CFM是等腰直角三角形,
∴CM= ,∴AE=CE= ,
∴AC=2 .
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
