22.1二次函数(4)—y=a(x-h)2的图象与性质课件人教版九年级数学上册(共14张PPT)
文档属性
| 名称 | 22.1二次函数(4)—y=a(x-h)2的图象与性质课件人教版九年级数学上册(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 255.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-13 10:48:24 | ||
图片预览






文档简介
(共14张PPT)
22.1 二次函数 的图象与性质
学习目标:
1.会用描点法画出二次函数 的图象;
2.能根据二次函数 的图象判断函数的性质;
3.能根据图象归纳出二次函数 与 的平移变化规律.
复习旧知
抛物线 a>0
图象 k>0
k<0
开口方向
对称轴
顶点坐标
函数的增减性
最值
x=0时,y最小值=k
当x<0时,y随x增大而减小;当x>0时,y随x增大而增大.
向上
y轴(直线 x=0)
(0,k)
上加下减!
上下
平移
第一步:列表
第二步:描点
x ··· -2 -1 0 1 2 3 4 ···
··· ···
第三步:连线
-4.5
-2
-0.5
0
-0.5
-2
-4.5
活动1:画出二次函数 的图象,并观察
总结 开口 方向 对称 轴 顶点 坐标 增减性 最值
下
x=1
(1,0)
当x>1时,
y随x的增大而减小
当x<1时,
y随x的增大而增大
当x=1时,y有最大值0
探索新知1:抛物线 的图象与性质
-1
3
1
O
-2
-2
-4
-6
4
-4
2
-3
-8
x
y
x ··· -4 -3 -2 -1 0 1 2 ···
··· ···
第一步:列表
第二步:描点
第三步:连线
-4.5
-2
-0.5
0
-0.5
-2
-4.5
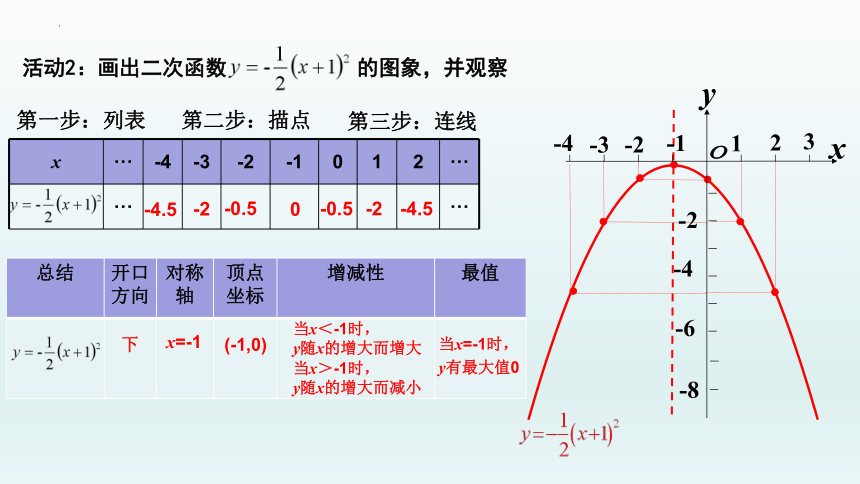
活动2:画出二次函数 的图象,并观察
总结 开口 方向 对称 轴 顶点 坐标 增减性 最值
下
x=-1
(-1,0)
当x<-1时,
y随x的增大而增大
当x>-1时,
y随x的增大而减小
当x=-1时,
y有最大值0
-1
3
1
O
-2
-2
-4
-6
-4
2
-3
-8
x
y
活动3:画出二次函数 , 的图象
x ··· -3 -2 -1 0 1 2 3 ···
··· ···
··· ···
2
0.5
0
0.5
2
4.5
8
8
4.5
0.5
2
0
0.5
2
总结 开口 方向 对称 轴 顶点 坐标 增减性 最值
上
x=-1
(-1,0)
当x>-1时,y随x的增大而增大
当x<-1时,y随x的增大而减小
当x=-1时,y有最小值0
上
x=1
(1,0)
当x>1时,y随x的增大而增大
当x<1时,y随x的增大而减小
当x=1时,y有最小值0
-1
3
1
O
-2
2
6
4
-4
2
4
-3
8
x
y
抛物线 a>0 a<0
图象 h>0
h<0
开口方向
对称轴
顶点坐标
函数的增减性
最值
x=h时,y最小值=0
x=h时,y最大值=0
当xh时,y随x增大而减小.
当xh时,y随x增大而增大.
向上
向下
直线 x=h
(h,0)
x
y
O
x
y
O
O
y
x
O
y
x
二次函数 的性质归纳:
y
O
-2
2
-2
-4
-6
4
-4
x=0
x=1
(0,0)
(1,0)
向右平移1个单位
向右平移1个单位
向右平移
1个单位
顶点坐标
对称轴
活动1:抛物线 与抛物线 有什么关系?
探索新知2:抛物线 的平移变化规律
猜想:
向右平移1个单位
函数
x
抛物线
抛物线
(0,0)
向左平移1个单位
(-1,0)
x=0
x=-1
-2
2
-2
-4
-6
4
-4
y
x
0
1
3
-1
-3
向左平移1个单位
猜想:
向左平移1个单位
向左平移
1个单位
顶点坐标
对称轴
函数
活动2:抛物线 与抛物线 有什么关系?
抛物线
抛物线
O
左加右减!
二次函数 与 的关系归纳:
向右平移
h(h>0)个单位
向左平移
h(h>0)个单位
x
y
抛物线
抛物线
抛物线
抛物线
下
直线x=2
(2,0)
上
直线x=-2
(-2,0)
1.抛物线y=-3(x-2)2开口向 ,
对称轴为___________,
顶点坐标为____________.
课堂练习
2.抛物线y=3(x+2)2开口向______,
对称轴为__________,
顶点坐标为__________.
a<0
a>0
y=a(x-h)2:对称轴直线x=h
y=a(x-h)2:顶点坐标(h,0)
y=3(x+2)2 化为 y=3[x-(-2)]2
3.将抛物线y=-2x2向左平移1个单位,再向右平移3个单位得抛物线解析式
_________________.
课堂练习
y=-2(x-2)2
y=-2x2
左1
左加右减
y=-2(x+1)2
右3
左加右减
y=-2(x+1-3)2
y=-2(x-2)2
化简
4.抛物线y=3(x+2)2 ,
当________时,y随x增大而增大,
当________,y随x增大而减小.
5.二次函数y=3(x+2)2最小值为______.
x>-2
x<-2
0
O
-2
x
y
课堂小结
1.二次函数 的性质:
开口方向、对称轴、顶点坐标、增减性、最值
3.思想方法总结:数形结合、从特殊到一般
2.二次函数 与 的平移变化规律:
左加右减,在x上加减
22.1 二次函数 的图象与性质
学习目标:
1.会用描点法画出二次函数 的图象;
2.能根据二次函数 的图象判断函数的性质;
3.能根据图象归纳出二次函数 与 的平移变化规律.
复习旧知
抛物线 a>0
图象 k>0
k<0
开口方向
对称轴
顶点坐标
函数的增减性
最值
x=0时,y最小值=k
当x<0时,y随x增大而减小;当x>0时,y随x增大而增大.
向上
y轴(直线 x=0)
(0,k)
上加下减!
上下
平移
第一步:列表
第二步:描点
x ··· -2 -1 0 1 2 3 4 ···
··· ···
第三步:连线
-4.5
-2
-0.5
0
-0.5
-2
-4.5
活动1:画出二次函数 的图象,并观察
总结 开口 方向 对称 轴 顶点 坐标 增减性 最值
下
x=1
(1,0)
当x>1时,
y随x的增大而减小
当x<1时,
y随x的增大而增大
当x=1时,y有最大值0
探索新知1:抛物线 的图象与性质
-1
3
1
O
-2
-2
-4
-6
4
-4
2
-3
-8
x
y
x ··· -4 -3 -2 -1 0 1 2 ···
··· ···
第一步:列表
第二步:描点
第三步:连线
-4.5
-2
-0.5
0
-0.5
-2
-4.5
活动2:画出二次函数 的图象,并观察
总结 开口 方向 对称 轴 顶点 坐标 增减性 最值
下
x=-1
(-1,0)
当x<-1时,
y随x的增大而增大
当x>-1时,
y随x的增大而减小
当x=-1时,
y有最大值0
-1
3
1
O
-2
-2
-4
-6
-4
2
-3
-8
x
y
活动3:画出二次函数 , 的图象
x ··· -3 -2 -1 0 1 2 3 ···
··· ···
··· ···
2
0.5
0
0.5
2
4.5
8
8
4.5
0.5
2
0
0.5
2
总结 开口 方向 对称 轴 顶点 坐标 增减性 最值
上
x=-1
(-1,0)
当x>-1时,y随x的增大而增大
当x<-1时,y随x的增大而减小
当x=-1时,y有最小值0
上
x=1
(1,0)
当x>1时,y随x的增大而增大
当x<1时,y随x的增大而减小
当x=1时,y有最小值0
-1
3
1
O
-2
2
6
4
-4
2
4
-3
8
x
y
抛物线 a>0 a<0
图象 h>0
h<0
开口方向
对称轴
顶点坐标
函数的增减性
最值
x=h时,y最小值=0
x=h时,y最大值=0
当x
当x
向上
向下
直线 x=h
(h,0)
x
y
O
x
y
O
O
y
x
O
y
x
二次函数 的性质归纳:
y
O
-2
2
-2
-4
-6
4
-4
x=0
x=1
(0,0)
(1,0)
向右平移1个单位
向右平移1个单位
向右平移
1个单位
顶点坐标
对称轴
活动1:抛物线 与抛物线 有什么关系?
探索新知2:抛物线 的平移变化规律
猜想:
向右平移1个单位
函数
x
抛物线
抛物线
(0,0)
向左平移1个单位
(-1,0)
x=0
x=-1
-2
2
-2
-4
-6
4
-4
y
x
0
1
3
-1
-3
向左平移1个单位
猜想:
向左平移1个单位
向左平移
1个单位
顶点坐标
对称轴
函数
活动2:抛物线 与抛物线 有什么关系?
抛物线
抛物线
O
左加右减!
二次函数 与 的关系归纳:
向右平移
h(h>0)个单位
向左平移
h(h>0)个单位
x
y
抛物线
抛物线
抛物线
抛物线
下
直线x=2
(2,0)
上
直线x=-2
(-2,0)
1.抛物线y=-3(x-2)2开口向 ,
对称轴为___________,
顶点坐标为____________.
课堂练习
2.抛物线y=3(x+2)2开口向______,
对称轴为__________,
顶点坐标为__________.
a<0
a>0
y=a(x-h)2:对称轴直线x=h
y=a(x-h)2:顶点坐标(h,0)
y=3(x+2)2 化为 y=3[x-(-2)]2
3.将抛物线y=-2x2向左平移1个单位,再向右平移3个单位得抛物线解析式
_________________.
课堂练习
y=-2(x-2)2
y=-2x2
左1
左加右减
y=-2(x+1)2
右3
左加右减
y=-2(x+1-3)2
y=-2(x-2)2
化简
4.抛物线y=3(x+2)2 ,
当________时,y随x增大而增大,
当________,y随x增大而减小.
5.二次函数y=3(x+2)2最小值为______.
x>-2
x<-2
0
O
-2
x
y
课堂小结
1.二次函数 的性质:
开口方向、对称轴、顶点坐标、增减性、最值
3.思想方法总结:数形结合、从特殊到一般
2.二次函数 与 的平移变化规律:
左加右减,在x上加减
同课章节目录
