2022年中考数学专题复习:二次函数综合--线段最大值(共14张PPT)
文档属性
| 名称 | 2022年中考数学专题复习:二次函数综合--线段最大值(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 381.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-13 10:51:58 | ||
图片预览



文档简介
(共14张PPT)
二次函数综合
专题复习
——线段的最大值问题
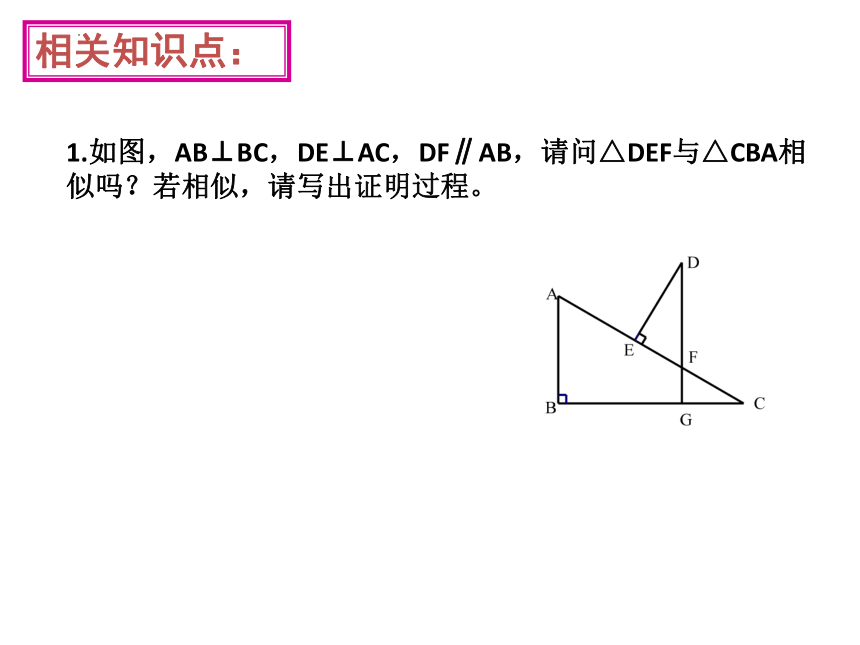
1.如图,AB⊥BC,DE⊥AC,DF∥AB,请问△DEF与△CBA相似吗?若相似,请写出证明过程。
相关知识点:
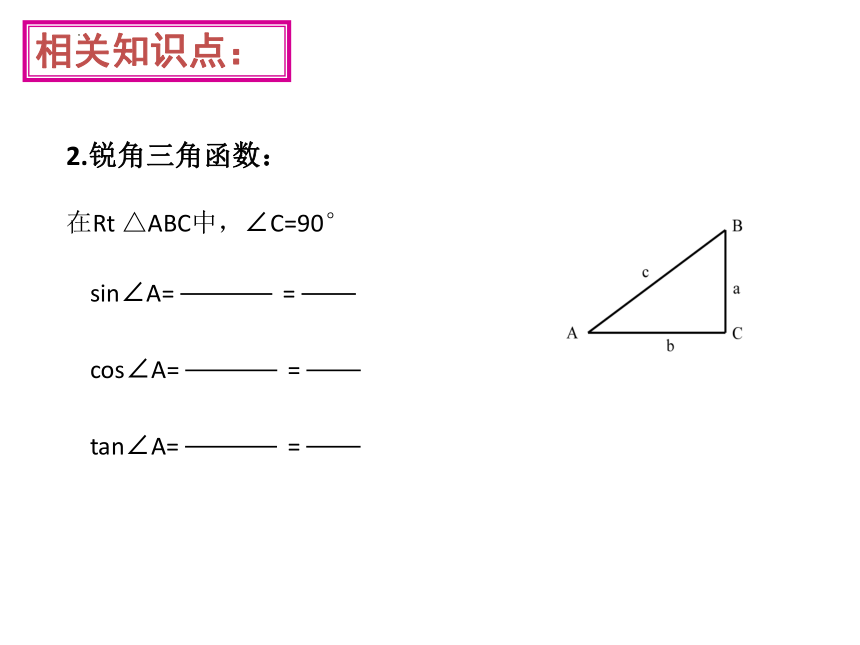
2.锐角三角函数:
在Rt △ABC中,∠C=90°
sin∠A= =
cos∠A= =
tan∠A= =
相关知识点:
②AB= .
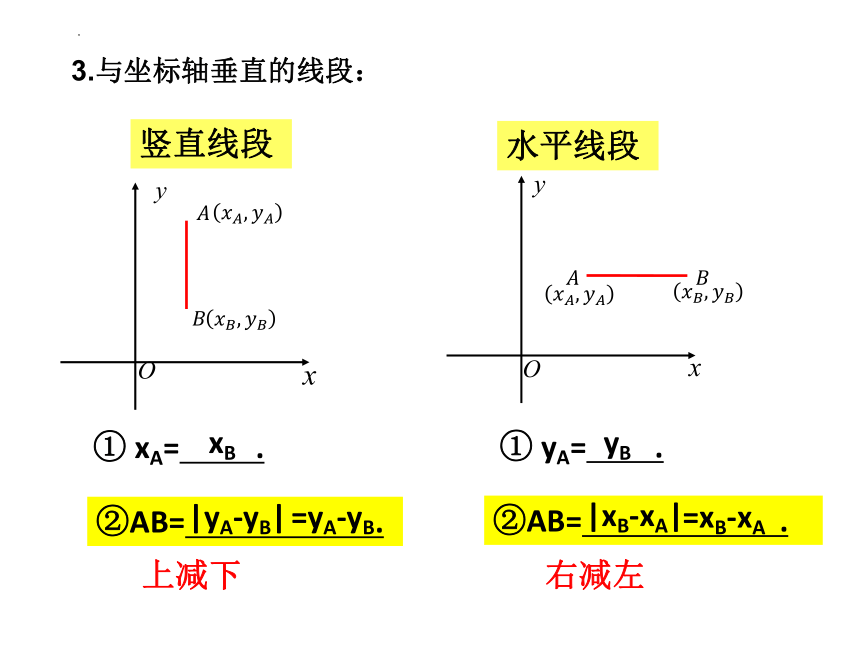
竖直线段
水平线段
上减下
右减左
① xA= .
① yA= .
②AB= .
3.与坐标轴垂直的线段:
xB
|yA-yB|
=yA-yB
|xB-xA|
=xB-xA
yB
例1(2019重庆B改编) 如图,二次函数y=-x2+2x+3与一次函数y=-x+3的图象交于B,C两点,点P是直线BC上方抛物线上一动点.
典型例题:
(1)过点P作PQ∥y轴
(2)过点P作PM∥x轴
设P( , )
∵PQ∥y轴
∴Q ( , )
∴PQ= .
设P( )
∵PM∥x轴
∴M ( , )
∴PM = .
与坐标轴平行的线段: 竖直线段;水平线段
追问:你能求出PQ的最大值了吗?
竖直线段
水平线段
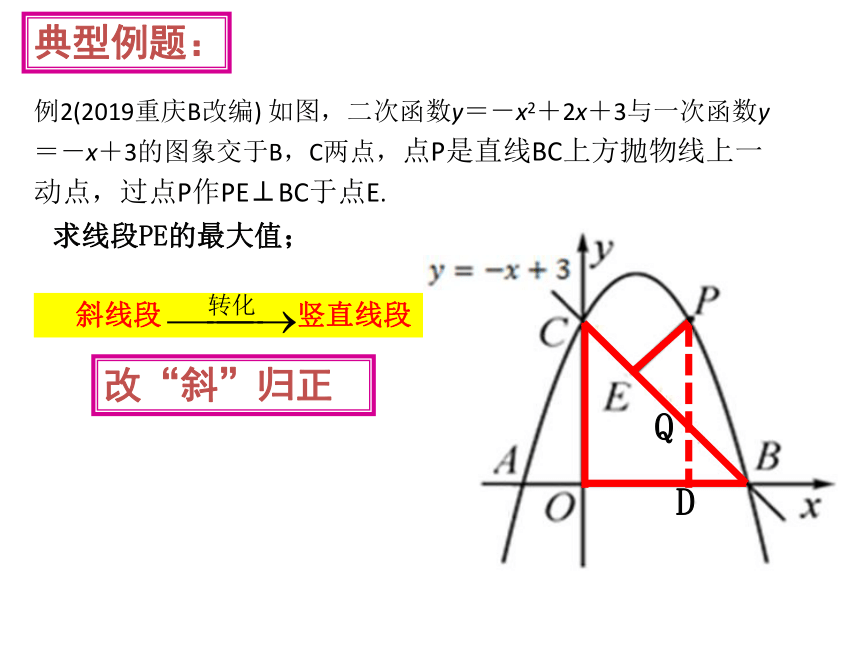
例2(2019重庆B改编) 如图,二次函数y=-x2+2x+3与一次函数y=-x+3的图象交于B,C两点,点P是直线BC上方抛物线上一动点,过点P作PE⊥BC于点E.
求线段PE的最大值;
斜线段 竖直线段
改“斜”归正
典型例题:
D
Q
例2(2019重庆B改编) 如图,二次函数y=-x2+2x+3与一次函数y=-x+3的图象交于B,C两点,点P是直线BC上方抛物线上一动点,过点P作PE⊥BC于点E.
求线段PE的最大值;
改“斜”归正
典型例题:
D
Q
解:
过点P作PD⊥x轴于点D,
交直线BC于点Q.
设P(m, -m2+2m+3),
则Q(m, -m+3)
∴PQ=-m2+2m+3 - (-m+3)
=-m2+3m
改“斜”归正
典型例题:
D
Q
∵B(3, 0),C(0, 3)
∴∠OBC=45°
∵PE⊥BC,PE⊥BC
∴∠EPQ=∠OBC=45°
在Rt△EPQ中
∴PE=PQ·cos∠EPQ
= (-m2+3m)
∴当m= 时,PE取得最大值为
此时P( , )
方法一:特殊角
∵PE⊥BC,PE⊥BC
改“斜”归正
典型例题:
D
Q
∴∠EPQ=∠OBC
在Rt△EPQ和Rt△OBC中
∴cos∠EPQ=cos∠OBC
即
∴PE= = (-m2+3m)
∴当m= 时,PE取得最大值为
此时P( , )
方法二:锐角三角函数
∵PE⊥BC,PE⊥BC
改“斜”归正
典型例题:
D
Q
∴∠PEQ=∠COB=90°,∠EPQ=∠OBC
∴Rt△EPQ∽Rt△OBC
∴
∴PE= = (-m2+3m)
∴当m= 时,PE取得最大值为
此时P( , )
方法三:相似三角形
变式:如图,二次函数 与一次函数 的图象交于B,C两点,点P是直线BC上方抛物线上一动点,过点P作PE⊥BC于点E,
变式:
(1) 求PE的最大值。
变式:如图,二次函数 与一次函数 的图象交于B,C两点,点P是直线BC上方抛物线上一动点,过点P作PE⊥BC于点E,
变式:
(1) 求PE的最大值。
Q
(2) 过P作PQ∥y轴交BC于点Q,
求△PEQ的周长的最大值。
三角形周长 竖直线段
AB=|y2-y1|
=y1-y2
小结:
1.与坐标轴平行的线段: 竖直线段;水平线段
三角形周长 竖直线段
三角形面积 竖直线段
改“斜”归正
斜线段 竖直线段
3.
2.
线段的最大值 函数的最大值
AB=|xB-xA|
=xB-xA
练习:
(2021重庆A改编) 如图,二次函数与一次函数图象相交于A,B两点,点P是直线AB下方抛物线上一动点.过点P作PD⊥AB,垂足为D,PM∥x轴,交AB于点M.
(1)求线段PD的最大值;
(2)当△PDM的周长取得最大值时,求点P的坐标和△PDM周长的最大值。
二次函数综合
专题复习
——线段的最大值问题
1.如图,AB⊥BC,DE⊥AC,DF∥AB,请问△DEF与△CBA相似吗?若相似,请写出证明过程。
相关知识点:
2.锐角三角函数:
在Rt △ABC中,∠C=90°
sin∠A= =
cos∠A= =
tan∠A= =
相关知识点:
②AB= .
竖直线段
水平线段
上减下
右减左
① xA= .
① yA= .
②AB= .
3.与坐标轴垂直的线段:
xB
|yA-yB|
=yA-yB
|xB-xA|
=xB-xA
yB
例1(2019重庆B改编) 如图,二次函数y=-x2+2x+3与一次函数y=-x+3的图象交于B,C两点,点P是直线BC上方抛物线上一动点.
典型例题:
(1)过点P作PQ∥y轴
(2)过点P作PM∥x轴
设P( , )
∵PQ∥y轴
∴Q ( , )
∴PQ= .
设P( )
∵PM∥x轴
∴M ( , )
∴PM = .
与坐标轴平行的线段: 竖直线段;水平线段
追问:你能求出PQ的最大值了吗?
竖直线段
水平线段
例2(2019重庆B改编) 如图,二次函数y=-x2+2x+3与一次函数y=-x+3的图象交于B,C两点,点P是直线BC上方抛物线上一动点,过点P作PE⊥BC于点E.
求线段PE的最大值;
斜线段 竖直线段
改“斜”归正
典型例题:
D
Q
例2(2019重庆B改编) 如图,二次函数y=-x2+2x+3与一次函数y=-x+3的图象交于B,C两点,点P是直线BC上方抛物线上一动点,过点P作PE⊥BC于点E.
求线段PE的最大值;
改“斜”归正
典型例题:
D
Q
解:
过点P作PD⊥x轴于点D,
交直线BC于点Q.
设P(m, -m2+2m+3),
则Q(m, -m+3)
∴PQ=-m2+2m+3 - (-m+3)
=-m2+3m
改“斜”归正
典型例题:
D
Q
∵B(3, 0),C(0, 3)
∴∠OBC=45°
∵PE⊥BC,PE⊥BC
∴∠EPQ=∠OBC=45°
在Rt△EPQ中
∴PE=PQ·cos∠EPQ
= (-m2+3m)
∴当m= 时,PE取得最大值为
此时P( , )
方法一:特殊角
∵PE⊥BC,PE⊥BC
改“斜”归正
典型例题:
D
Q
∴∠EPQ=∠OBC
在Rt△EPQ和Rt△OBC中
∴cos∠EPQ=cos∠OBC
即
∴PE= = (-m2+3m)
∴当m= 时,PE取得最大值为
此时P( , )
方法二:锐角三角函数
∵PE⊥BC,PE⊥BC
改“斜”归正
典型例题:
D
Q
∴∠PEQ=∠COB=90°,∠EPQ=∠OBC
∴Rt△EPQ∽Rt△OBC
∴
∴PE= = (-m2+3m)
∴当m= 时,PE取得最大值为
此时P( , )
方法三:相似三角形
变式:如图,二次函数 与一次函数 的图象交于B,C两点,点P是直线BC上方抛物线上一动点,过点P作PE⊥BC于点E,
变式:
(1) 求PE的最大值。
变式:如图,二次函数 与一次函数 的图象交于B,C两点,点P是直线BC上方抛物线上一动点,过点P作PE⊥BC于点E,
变式:
(1) 求PE的最大值。
Q
(2) 过P作PQ∥y轴交BC于点Q,
求△PEQ的周长的最大值。
三角形周长 竖直线段
AB=|y2-y1|
=y1-y2
小结:
1.与坐标轴平行的线段: 竖直线段;水平线段
三角形周长 竖直线段
三角形面积 竖直线段
改“斜”归正
斜线段 竖直线段
3.
2.
线段的最大值 函数的最大值
AB=|xB-xA|
=xB-xA
练习:
(2021重庆A改编) 如图,二次函数与一次函数图象相交于A,B两点,点P是直线AB下方抛物线上一动点.过点P作PD⊥AB,垂足为D,PM∥x轴,交AB于点M.
(1)求线段PD的最大值;
(2)当△PDM的周长取得最大值时,求点P的坐标和△PDM周长的最大值。
同课章节目录
