北京版八年级数学下册15.5 三角形中位线定理教学设计
文档属性
| 名称 | 北京版八年级数学下册15.5 三角形中位线定理教学设计 | 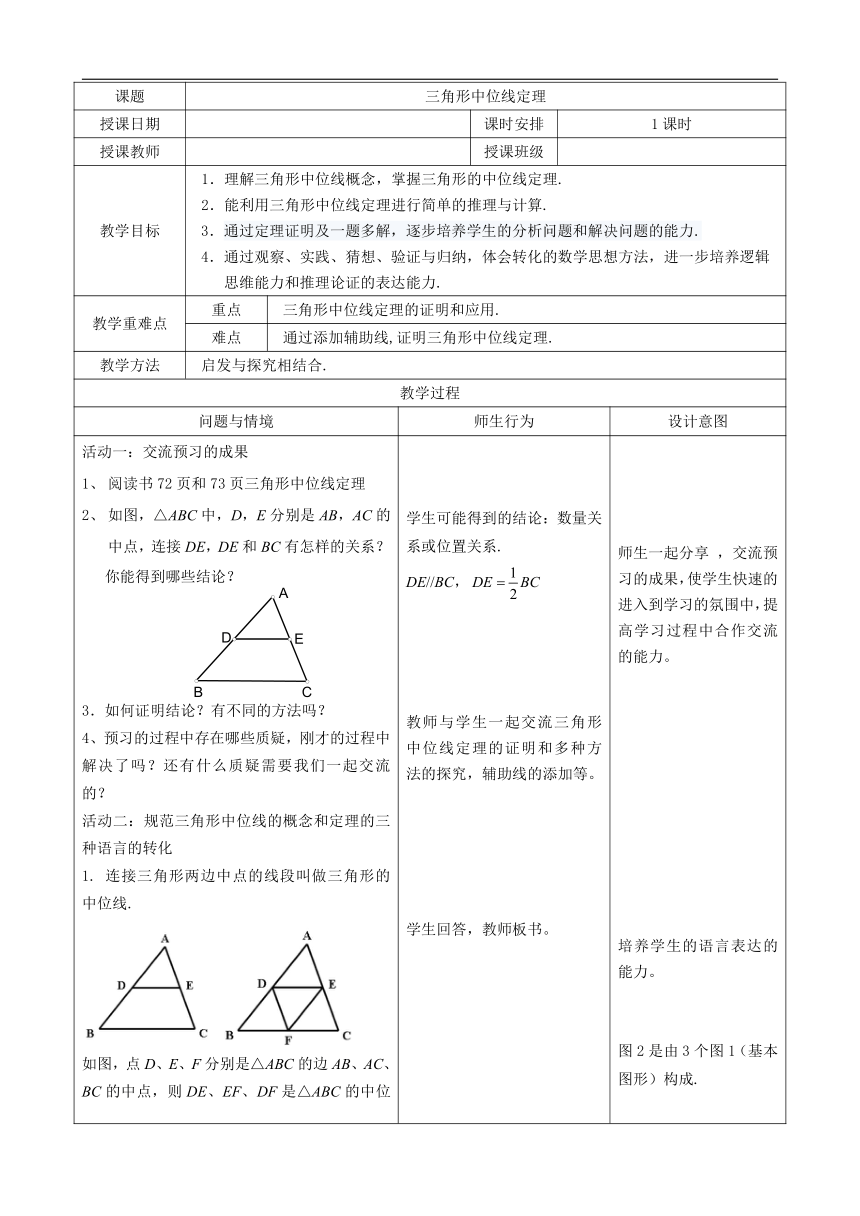 | |
| 格式 | doc | ||
| 文件大小 | 101.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-13 12:50:33 | ||
图片预览

文档简介
课题 三角形中位线定理
授课日期 课时安排 1课时
授课教师 授课班级
教学目标 1.理解三角形中位线概念,掌握三角形的中位线定理.2.能利用三角形中位线定理进行简单的推理与计算.3.通过定理证明及一题多解,逐步培养学生的分析问题和解决问题的能力.4.通过观察、实践、猜想、验证与归纳,体会转化的数学思想方法,进一步培养逻辑思维能力和推理论证的表达能力.
教学重难点 重点 三角形中位线定理的证明和应用.
难点 通过添加辅助线,证明三角形中位线定理.
教学方法 启发与探究相结合.
教学过程
问题与情境 师生行为 设计意图
活动一:交流预习的成果阅读书72页和73页三角形中位线定理如图,△ABC中,D,E分别是AB,AC的中点,连接DE,DE和BC有怎样的关系?你能得到哪些结论?3.如何证明结论?有不同的方法吗?4、预习的过程中存在哪些质疑,刚才的过程中解决了吗?还有什么质疑需要我们一起交流的?活动二:规范三角形中位线的概念和定理的三种语言的转化1. 连接三角形两边中点的线段叫做三角形的中位线.如图,点D、E、F分别是△ABC的边AB、AC、BC的中点,则DE、EF、DF是△ABC的中位线.一个三角形有3条中位线.2.三角形的中位线和三角形的中线一样吗?有什么区别和联系?3. 三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.符号语言:如图,△ABC中,D、E分别是的边AB、AC的中点,则DE//BC,.4三角形中位线成立的条件、结论和作用:条件:连接两边中点得到中位线结论:位置关系和数量关系,根据题目需要选用作用:在解决“倍分”问题的时候?或问题中有中点时通常要考虑用三角形的中位线。 学生可能得到的结论:数量关系或位置关系.DE//BC,教师与学生一起交流三角形中位线定理的证明和多种方法的探究,辅助线的添加等。学生回答,教师板书。学生画图,回答问题,教师引导,归纳.学生尝试描述三角形中位线定理(文字语言与数学语言),教师板书. 师生一起分享 ,交流预习的成果,使学生快速的进入到学习的氛围中,提高学习过程中合作交流的能力。培养学生的语言表达的能力。图2是由3个图1(基本图形)构成.区分三角形中位线和三角形中线的概念。揭示定理适用的条件.结论中既有位置关系又有数量关系.剖析定理的内容,分析定理的作用。
活动三:运用定理,解决问题1、思考:如图,A、B两地被池溏隔开,在没有任何测量工具的情况下,小明通过下面的方法估测出了A、B间的距离,先在AB外选一点C,然后步测出AC、BC的中点M、N,并测出了MN的长,由此他就知道了A、B间的距离,你能说说其中的道理吗 2.例:如图,△ABC中,D,E,F分别是AB,AC,BC的中点,DE与AF相交于点O.求证:DE与AF互相平分. 学生在学案上独立完成,教师巡视并适当点拨.学生交流思考过程,展示答案.学生先进行分析,由已知想可知,由未知想需知,随后教师引导辅助线的添加,解决问题 关注学生对三角形中位线的识别,找到基本图形,利用中位线定理得到位置和数量关系.锻炼学生的思维能力,调动学生的学习兴趣.通过添加辅助线还原定理的基本图形,进而解决问题.引导学生注意图形的联系,体现转化的思想.在解决与中点有关的问题中,往往可以通过构造三角形的中位线(或第三边)来得到线段倍分或平行的结论.
3.小结:⑴三角形的中位线是三角形中一种重要的线段,要能区分于三角形的中线; ⑵三角形的中位线定理是三角形的一个重要性质定理。注意定理的结论之一是平行关系,结论之二是线段的倍分关系。具体应用时,可视具体情况,选用其中一个关系或用两个关系。⑶在处理问题时,要求同时出现三角形及中位线①有中点连线而无三角形,要作辅助线产生三角形②有三角形而无中位线,要连结两边中点得中位线。 师生一起对本节课的内容进行反思,从过程、方法和定理的作用三方面进行小结,梳理本节课的内容。 引导学生从知识、方法、思想上对本课内容进行总结,包括对三角形中位线定理的基本图形的识别,以及通过添加辅助线构造(还原)基本图形,体会转化的数学思想.
4.练习:⑴已知三角形各边的长分别为 6cm,8 cm 和 10 cm ,连接各边中点所成三角形的周长是 ⑵如图,四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点. 试探究四边形EFGH的形状.
作业:练习册:48页
板书设计 三角形中位线定理三角形中位线概念 三、定理的证明方法 四、例题三角形中位线定理
授课日期 课时安排 1课时
授课教师 授课班级
教学目标 1.理解三角形中位线概念,掌握三角形的中位线定理.2.能利用三角形中位线定理进行简单的推理与计算.3.通过定理证明及一题多解,逐步培养学生的分析问题和解决问题的能力.4.通过观察、实践、猜想、验证与归纳,体会转化的数学思想方法,进一步培养逻辑思维能力和推理论证的表达能力.
教学重难点 重点 三角形中位线定理的证明和应用.
难点 通过添加辅助线,证明三角形中位线定理.
教学方法 启发与探究相结合.
教学过程
问题与情境 师生行为 设计意图
活动一:交流预习的成果阅读书72页和73页三角形中位线定理如图,△ABC中,D,E分别是AB,AC的中点,连接DE,DE和BC有怎样的关系?你能得到哪些结论?3.如何证明结论?有不同的方法吗?4、预习的过程中存在哪些质疑,刚才的过程中解决了吗?还有什么质疑需要我们一起交流的?活动二:规范三角形中位线的概念和定理的三种语言的转化1. 连接三角形两边中点的线段叫做三角形的中位线.如图,点D、E、F分别是△ABC的边AB、AC、BC的中点,则DE、EF、DF是△ABC的中位线.一个三角形有3条中位线.2.三角形的中位线和三角形的中线一样吗?有什么区别和联系?3. 三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.符号语言:如图,△ABC中,D、E分别是的边AB、AC的中点,则DE//BC,.4三角形中位线成立的条件、结论和作用:条件:连接两边中点得到中位线结论:位置关系和数量关系,根据题目需要选用作用:在解决“倍分”问题的时候?或问题中有中点时通常要考虑用三角形的中位线。 学生可能得到的结论:数量关系或位置关系.DE//BC,教师与学生一起交流三角形中位线定理的证明和多种方法的探究,辅助线的添加等。学生回答,教师板书。学生画图,回答问题,教师引导,归纳.学生尝试描述三角形中位线定理(文字语言与数学语言),教师板书. 师生一起分享 ,交流预习的成果,使学生快速的进入到学习的氛围中,提高学习过程中合作交流的能力。培养学生的语言表达的能力。图2是由3个图1(基本图形)构成.区分三角形中位线和三角形中线的概念。揭示定理适用的条件.结论中既有位置关系又有数量关系.剖析定理的内容,分析定理的作用。
活动三:运用定理,解决问题1、思考:如图,A、B两地被池溏隔开,在没有任何测量工具的情况下,小明通过下面的方法估测出了A、B间的距离,先在AB外选一点C,然后步测出AC、BC的中点M、N,并测出了MN的长,由此他就知道了A、B间的距离,你能说说其中的道理吗 2.例:如图,△ABC中,D,E,F分别是AB,AC,BC的中点,DE与AF相交于点O.求证:DE与AF互相平分. 学生在学案上独立完成,教师巡视并适当点拨.学生交流思考过程,展示答案.学生先进行分析,由已知想可知,由未知想需知,随后教师引导辅助线的添加,解决问题 关注学生对三角形中位线的识别,找到基本图形,利用中位线定理得到位置和数量关系.锻炼学生的思维能力,调动学生的学习兴趣.通过添加辅助线还原定理的基本图形,进而解决问题.引导学生注意图形的联系,体现转化的思想.在解决与中点有关的问题中,往往可以通过构造三角形的中位线(或第三边)来得到线段倍分或平行的结论.
3.小结:⑴三角形的中位线是三角形中一种重要的线段,要能区分于三角形的中线; ⑵三角形的中位线定理是三角形的一个重要性质定理。注意定理的结论之一是平行关系,结论之二是线段的倍分关系。具体应用时,可视具体情况,选用其中一个关系或用两个关系。⑶在处理问题时,要求同时出现三角形及中位线①有中点连线而无三角形,要作辅助线产生三角形②有三角形而无中位线,要连结两边中点得中位线。 师生一起对本节课的内容进行反思,从过程、方法和定理的作用三方面进行小结,梳理本节课的内容。 引导学生从知识、方法、思想上对本课内容进行总结,包括对三角形中位线定理的基本图形的识别,以及通过添加辅助线构造(还原)基本图形,体会转化的数学思想.
4.练习:⑴已知三角形各边的长分别为 6cm,8 cm 和 10 cm ,连接各边中点所成三角形的周长是 ⑵如图,四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点. 试探究四边形EFGH的形状.
作业:练习册:48页
板书设计 三角形中位线定理三角形中位线概念 三、定理的证明方法 四、例题三角形中位线定理
同课章节目录
