第八章 成对数据的统计分析 小结 课件(共28张PPT)
文档属性
| 名称 | 第八章 成对数据的统计分析 小结 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-13 10:06:35 | ||
图片预览







文档简介
(共28张PPT)
第八章 成对数据的统计分析小结
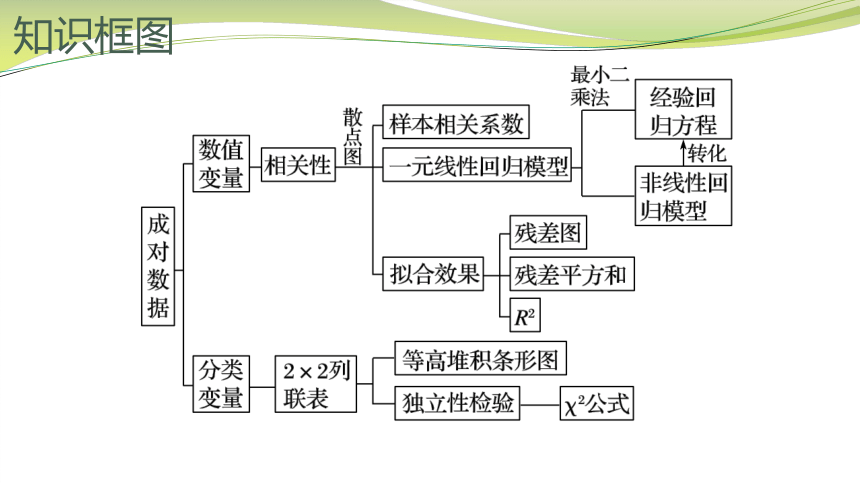
知识框图
一、变量的相关性
1.变量的相关关系与样本相关系数是学习一元线性回归模型的前提和基础,前者可借助散点图从直观上分析变量间的相关性,后者从数量上准确刻化了两个变量的相关程度.
2.在学习该部分知识时,体会直观想象和数学运算的素养.
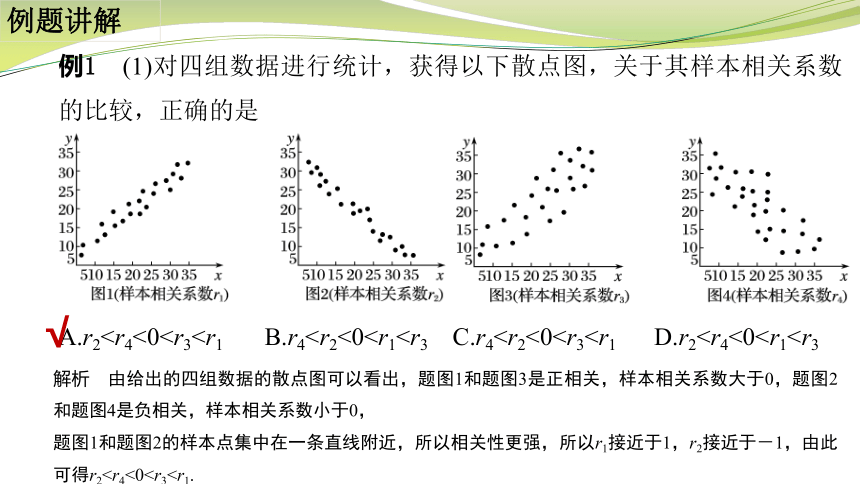
例1 (1)对四组数据进行统计,获得以下散点图,关于其样本相关系数的比较,正确的是
A.r2√
例题讲解
解析 由给出的四组数据的散点图可以看出,题图1和题图3是正相关,样本相关系数大于0,题图2和题图4是负相关,样本相关系数小于0,
题图1和题图2的样本点集中在一条直线附近,所以相关性更强,所以r1接近于1,r2接近于-1,由此可得r2(2)在一次试验中,测得(x,y)的四组值分别为(1,2),(2,0),(4,-4),(-1,6),则y与x的样本相关系数为_____.
-1
方法二 观察四个点,发现其在一条单调递减的直线上,
故y与x的样本相关系数为-1.
例题讲解
变量相关性的判断的两种方法
(1)散点图法:直观形象.
(2)公式法:可用公式精确计算相关系数
反思感悟:
样本相关系数r的取值范围为 .
当|r|越接近1时,成对样本数据的线性相关程度越 ;
当|r|越接近0时,成对样本数据的线性相关程度越 .
注意点:
当|r|=1时,表明成对样本数据都在一条直线上,即两个变量之间满足一种线性关系.
当r=0时,表明成对数据间没有线性相关关系,但不排除它们之间有其他相关关系.
[-1,1]
强
弱
二、一元线性回归模型及其应用
1.该知识点是具有线性相关关系的两变量的一种拟合应用,
目的是借助函数的思想对实际问题做出预测和分析.
2.主要培养数学建模和数据分析的素养.
例2.(1)已知x与y之间的成对样本数据:
√
x 0 1 2 3
y m 3 5.5 7
例题讲解
√
例题讲解
例3 一商场对每天进店人数和商品销售件数进行了统计对比,得到如下表格:
人数xi 10 15 20 25 30 35 40
件数yi 4 7 12 15 20 23 27
其中i=1,2,3,4,5,6,7.
(1)以每天进店人数为横坐标,每天商品销售件数为纵坐标,画出散点图;
例题讲解
解 由表中数据,画出7个数据点,
可得散点图如图所示.
例题讲解
(2)求经验回归方程;(结果保留到小数点后两位)
例题讲解
例题讲解
(3)预测进店人数为80时商品销售的件数.(结果保留整数)
例题讲解
反思感悟
解决回归分析问题的一般步骤
(1)画散点图.根据已知数据画出散点图.
(2)判断变量的相关性并求经验回归方程.通过观察散点图,直观感知两个变量是否具有相关关系;在此基础上,利用最小二乘法求回归系数,然后写出经验回归方程.
(3)回归分析.画残差图或计算R2,进行残差分析.
(4)实际应用.依据求得的经验回归方程解决实际问题.
反思感悟:
三、独立性检验
1.主要考查根据样本制作2×2列联表,由2×2列联表计算χ2,查表分析并判断相关性结论的可信程度.
2.通过计算χ2值,进而分析相关性结论的可信程度,提升数学运算、数据分析素养.
例4:为了解某班学生喜爱打篮球是否与性别有关联,对本班50人进行问卷调查得到了如下的列联表:
性别 喜爱打篮球 不喜爱打篮球 合计
男生 5
女生 10
合计 50
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为0.6.
(1)请将上面的列联表补充完整(不用写计算过程).
(2)依据α=0.01的独立性检验,能否认为喜爱打篮球与性别有关联 说明你的理由.
例题讲解
解:(1)依题意可知喜爱打篮球的学生的人数为50×0.6=30.
列联表补充如下:
性别 喜爱打篮球 不喜爱打篮球 合计
男生 20 5 25
女生 10 15 25
合计 30 20 50
(2)零假设为H0:喜爱打篮球与性别无关联.根据列表中的数据,经计算得到:
依据α=0.01的独立性检验,我们推断H0不成立,而且此推断犯错误的概率不超过0.01,即认为喜爱打篮球与性别有关联.
男生中喜爱打篮球和不喜爱打篮球的频率分别为20/25=4/5和5/25=1/5;
女生中喜爱打篮球和不喜爱打篮球的频率分别为10/25=2/5和15/25=3/5.
男生比女生更喜爱打篮球.
例题讲解
频率分析:
结论:
例5:学校举行运动会,为了搞好接待工作,组委会招募了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余人不喜爱运动.
(1)根据以上数据完成以下2×2列联表:
运动的喜好 合计
喜爱运动 不喜爱运动
男 10 16
女 6 14
合计 30
解
喜爱运动 不喜爱运动 合计
男 10 6 16
女 6 8 14
合计 16 14 30
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.10的前提下认为性别与喜爱运动有关?
解 零假设为H0:喜爱运动与性别无关,由已知数据可得
因为1.157 5<2.706=x0.1,根据小概率值α=0.1的独立性检验,没有充分证据推断H0不成立,即认为性别与喜爱运动无关.
反思感悟:
(1)提出零假设H0:X和Y相互独立,并给出在问题中的解释.
(2)根据抽样数据整理出2×2列联表,计算的值,并与临界值比较.
(3)根据检验规则得出推断结论.
(4)在X和Y不独立的情况下,根据需要,通过比较相应的频率,分析X和Y间的影响规律.
应用独立性检验解决实际问题大致应包括以下几个主要环节:
四 综合应用
身高较矮 身高较高 合计
体重较轻
体重较重
合计
身高较矮 身高较高 合计
体重较轻 6 15 21
体重较重 6 5 11
合计 12 20 32
解析: (1)列联表如下:
编号 1 2 3 4 5 6 7 8
身高 166 167 160 173 178 169 158 173
体重 57 58 53 61 66 57 50 66
编号 1 2 3 4 5 6 7 8
体重 57 58 53 61 66 57 50 66
残差 0.1 0.3 0.9 —1.5 —0.5
解析: (2)
编号 1 2 3 4 5 6 7 8
身高 166 167 160 173 178 169 158 173
体重 57 58 53 61 66 57 50 66
解析:
谢谢观看!
第八章 成对数据的统计分析小结
知识框图
一、变量的相关性
1.变量的相关关系与样本相关系数是学习一元线性回归模型的前提和基础,前者可借助散点图从直观上分析变量间的相关性,后者从数量上准确刻化了两个变量的相关程度.
2.在学习该部分知识时,体会直观想象和数学运算的素养.
例1 (1)对四组数据进行统计,获得以下散点图,关于其样本相关系数的比较,正确的是
A.r2
例题讲解
解析 由给出的四组数据的散点图可以看出,题图1和题图3是正相关,样本相关系数大于0,题图2和题图4是负相关,样本相关系数小于0,
题图1和题图2的样本点集中在一条直线附近,所以相关性更强,所以r1接近于1,r2接近于-1,由此可得r2
-1
方法二 观察四个点,发现其在一条单调递减的直线上,
故y与x的样本相关系数为-1.
例题讲解
变量相关性的判断的两种方法
(1)散点图法:直观形象.
(2)公式法:可用公式精确计算相关系数
反思感悟:
样本相关系数r的取值范围为 .
当|r|越接近1时,成对样本数据的线性相关程度越 ;
当|r|越接近0时,成对样本数据的线性相关程度越 .
注意点:
当|r|=1时,表明成对样本数据都在一条直线上,即两个变量之间满足一种线性关系.
当r=0时,表明成对数据间没有线性相关关系,但不排除它们之间有其他相关关系.
[-1,1]
强
弱
二、一元线性回归模型及其应用
1.该知识点是具有线性相关关系的两变量的一种拟合应用,
目的是借助函数的思想对实际问题做出预测和分析.
2.主要培养数学建模和数据分析的素养.
例2.(1)已知x与y之间的成对样本数据:
√
x 0 1 2 3
y m 3 5.5 7
例题讲解
√
例题讲解
例3 一商场对每天进店人数和商品销售件数进行了统计对比,得到如下表格:
人数xi 10 15 20 25 30 35 40
件数yi 4 7 12 15 20 23 27
其中i=1,2,3,4,5,6,7.
(1)以每天进店人数为横坐标,每天商品销售件数为纵坐标,画出散点图;
例题讲解
解 由表中数据,画出7个数据点,
可得散点图如图所示.
例题讲解
(2)求经验回归方程;(结果保留到小数点后两位)
例题讲解
例题讲解
(3)预测进店人数为80时商品销售的件数.(结果保留整数)
例题讲解
反思感悟
解决回归分析问题的一般步骤
(1)画散点图.根据已知数据画出散点图.
(2)判断变量的相关性并求经验回归方程.通过观察散点图,直观感知两个变量是否具有相关关系;在此基础上,利用最小二乘法求回归系数,然后写出经验回归方程.
(3)回归分析.画残差图或计算R2,进行残差分析.
(4)实际应用.依据求得的经验回归方程解决实际问题.
反思感悟:
三、独立性检验
1.主要考查根据样本制作2×2列联表,由2×2列联表计算χ2,查表分析并判断相关性结论的可信程度.
2.通过计算χ2值,进而分析相关性结论的可信程度,提升数学运算、数据分析素养.
例4:为了解某班学生喜爱打篮球是否与性别有关联,对本班50人进行问卷调查得到了如下的列联表:
性别 喜爱打篮球 不喜爱打篮球 合计
男生 5
女生 10
合计 50
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为0.6.
(1)请将上面的列联表补充完整(不用写计算过程).
(2)依据α=0.01的独立性检验,能否认为喜爱打篮球与性别有关联 说明你的理由.
例题讲解
解:(1)依题意可知喜爱打篮球的学生的人数为50×0.6=30.
列联表补充如下:
性别 喜爱打篮球 不喜爱打篮球 合计
男生 20 5 25
女生 10 15 25
合计 30 20 50
(2)零假设为H0:喜爱打篮球与性别无关联.根据列表中的数据,经计算得到:
依据α=0.01的独立性检验,我们推断H0不成立,而且此推断犯错误的概率不超过0.01,即认为喜爱打篮球与性别有关联.
男生中喜爱打篮球和不喜爱打篮球的频率分别为20/25=4/5和5/25=1/5;
女生中喜爱打篮球和不喜爱打篮球的频率分别为10/25=2/5和15/25=3/5.
男生比女生更喜爱打篮球.
例题讲解
频率分析:
结论:
例5:学校举行运动会,为了搞好接待工作,组委会招募了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余人不喜爱运动.
(1)根据以上数据完成以下2×2列联表:
运动的喜好 合计
喜爱运动 不喜爱运动
男 10 16
女 6 14
合计 30
解
喜爱运动 不喜爱运动 合计
男 10 6 16
女 6 8 14
合计 16 14 30
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.10的前提下认为性别与喜爱运动有关?
解 零假设为H0:喜爱运动与性别无关,由已知数据可得
因为1.157 5<2.706=x0.1,根据小概率值α=0.1的独立性检验,没有充分证据推断H0不成立,即认为性别与喜爱运动无关.
反思感悟:
(1)提出零假设H0:X和Y相互独立,并给出在问题中的解释.
(2)根据抽样数据整理出2×2列联表,计算的值,并与临界值比较.
(3)根据检验规则得出推断结论.
(4)在X和Y不独立的情况下,根据需要,通过比较相应的频率,分析X和Y间的影响规律.
应用独立性检验解决实际问题大致应包括以下几个主要环节:
四 综合应用
身高较矮 身高较高 合计
体重较轻
体重较重
合计
身高较矮 身高较高 合计
体重较轻 6 15 21
体重较重 6 5 11
合计 12 20 32
解析: (1)列联表如下:
编号 1 2 3 4 5 6 7 8
身高 166 167 160 173 178 169 158 173
体重 57 58 53 61 66 57 50 66
编号 1 2 3 4 5 6 7 8
体重 57 58 53 61 66 57 50 66
残差 0.1 0.3 0.9 —1.5 —0.5
解析: (2)
编号 1 2 3 4 5 6 7 8
身高 166 167 160 173 178 169 158 173
体重 57 58 53 61 66 57 50 66
解析:
谢谢观看!
