沪科版数学八年级下册 19.2 平行四边形复习教案
文档属性
| 名称 | 沪科版数学八年级下册 19.2 平行四边形复习教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 158.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-13 11:38:39 | ||
图片预览

文档简介
“平行四边形”复习教学设计
内容分析:
由于沪科版数学第19章平行四边形、矩形、菱形、正方形包含定义、性质、判定以及应用,内容繁多而又容易混淆,因此这一节课我来带领同学们把这些特殊四边形的内容进行一次系统的复习。本章一开始学习了“多边形”,接着介绍特殊的多边形即平行四边形的定义、性质、判定,最后有平行四边形出发,介绍了矩形、菱形、正方形的定义、性质、判定等,最后介绍综合运用。
教学目标:
1、建立平行四边形及特殊平行四边形的知识框架,掌握平行四边形及特殊平行四边形的判定,并能熟练应用。
2、掌握解决平行四边形问题的一般方法。
3、运用图形的变换探索图形特征与性质,体会数学研究和发现的过程,领悟知识的生成,发展与变化,发展空间观念。
教学重点:
掌握解决平行四边形问题的一般方法,能够从边、角、对角线三个方面思考问题。
教学难点:
平行四边形有关知识的综合运用。
教学过程:
本节课设计了五个环节,第一个环节——温故知新,第二个环节——应用举例,第三个环节——训练巩固,第四个环节——课堂小结,第五个环节——布置作业。
第一个环节:温故知新
教师出示表格,学生完成填空。
平行四边形定义:
平行四边形性质:分别从边、角、对角线方面引导学生回忆,请学生逐一回答,师生共同评价与补充。
平行四边形判定:分别从边与边、对角线相互关系方面引导学生回忆,请学生逐一回答,师生共同评价与补充。
教师用大屏幕展示一般平行四边形变成为矩形的变化图,让学生感受矩形与一般平行四边形的核心区别,增加对矩形的印象。
让一学生回忆矩形的定义,从矩形的边、角、对角线三个方面加以回忆矩形的性质与判定(用红色字体突出矩形的特殊性质,以引起学生有意注意,提高复习效率)。
让学生分别回忆菱形与正方形的定义、性质、判定(也用红色字体突出特殊性质)。
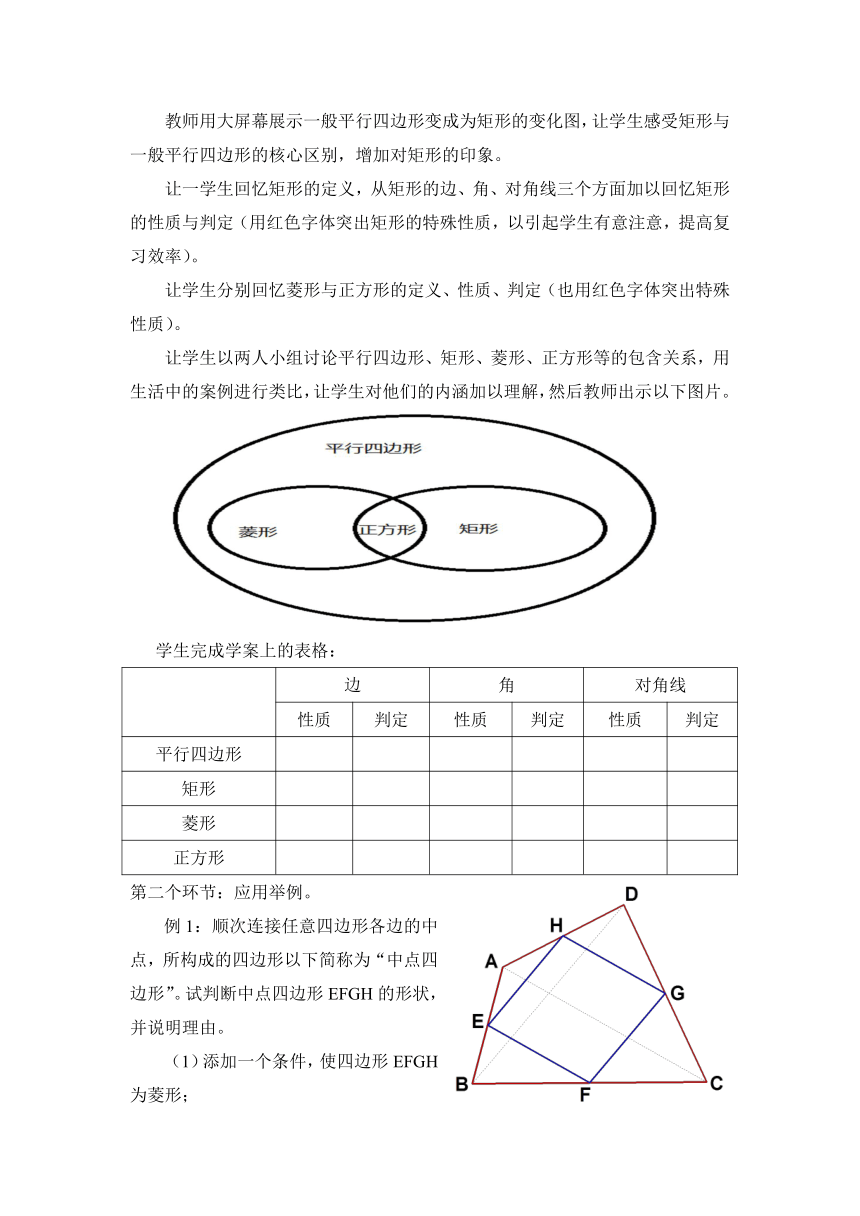
让学生以两人小组讨论平行四边形、矩形、菱形、正方形等的包含关系,用生活中的案例进行类比,让学生对他们的内涵加以理解,然后教师出示以下图片。
学生完成学案上的表格:
边 角 对角线
性质 判定 性质 判定 性质 判定
平行四边形
矩形
菱形
正方形
第二个环节:应用举例。
例1:顺次连接任意四边形各边的中点,所构成的四边形以下简称为“中点四边形”。试判断中点四边形EFGH的形状,并说明理由。
(1)添加一个条件,使四边形EFGH为菱形;
(2)添加一个条件,使四边形EFGH为矩形;
(3)添加一个条件,使四边形EFGH为正方形。
教师活动:教师先要求学生打开课本,反倒第77页,带领学生回忆“中点三角形”,分析中点三角形的特点,从而引出“中点四边形”的定义。
学生活动:学生两人一组探究中点四边形的性质,完成上述例题。
师生共同总结:
1顺次连接任意的四边形各边中点得平行四边形;
2顺次连接对角线相等的四边形各边中点得菱形;
3顺次连接对角线互相垂直的四边形各边中点得矩形;
4顺次连接对角线相等且互相垂直的四边形各边中点得正方形。
问题:那么,特殊平行四边形的“中点四边形”会是怎样的图形呢?
1.矩形的“中点四边形”是 形;
2.菱形的“中点四边形”是 形;
3.正方形的“中点四边形”是 形。
思考题:在矩形ABCD中,AB=16,BC=8.将矩形沿AC折叠,点D落在点E处,且CE交AB于点F,求AF的长。
点拨:对于折叠问题,可以从折叠前后的两个图形是全等图形入手进行分析,引导学生利用“双平”模型研究此类问题。
第三环节:训练巩固
1、检查一个门框是矩形的方法是( )
A、测量两条对角线是否相等.
B、测量有三个角是直角.
C、 测量两条对角线是否互相平分.
D、 测量两条对角线是否互相垂直.
2、顺次连接矩形各边中点所得的四边形是( )
A、矩形 B、菱形 C、梯形 D、正方形
思考题:如图,在□ABCD中,E、F、G、H分别是四条边上的点,且满足BE=DF,CG=AH,连接EF、GH。试说明:EF与GH互相平分。
第四个环节:课堂小结
通过本节课的复习,你取得了哪些经验?
活动目的:培养学生的语言组织能力、自我表现能力、综合能力,同时也检测了学生听课的认真程度,从学生的回答中了解不同程度的学生对这节课内容掌握的程度。
(
B
F
C
D
E
A
)第五个环节:布置作业
如图,已知AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F。
求证:①四边形AEDF是菱形
②连接EF,若AE=8,AD=12,求EF的长。
③当△ABC满足什么条件时,四边形AEDF是正方形?说明理由。
内容分析:
由于沪科版数学第19章平行四边形、矩形、菱形、正方形包含定义、性质、判定以及应用,内容繁多而又容易混淆,因此这一节课我来带领同学们把这些特殊四边形的内容进行一次系统的复习。本章一开始学习了“多边形”,接着介绍特殊的多边形即平行四边形的定义、性质、判定,最后有平行四边形出发,介绍了矩形、菱形、正方形的定义、性质、判定等,最后介绍综合运用。
教学目标:
1、建立平行四边形及特殊平行四边形的知识框架,掌握平行四边形及特殊平行四边形的判定,并能熟练应用。
2、掌握解决平行四边形问题的一般方法。
3、运用图形的变换探索图形特征与性质,体会数学研究和发现的过程,领悟知识的生成,发展与变化,发展空间观念。
教学重点:
掌握解决平行四边形问题的一般方法,能够从边、角、对角线三个方面思考问题。
教学难点:
平行四边形有关知识的综合运用。
教学过程:
本节课设计了五个环节,第一个环节——温故知新,第二个环节——应用举例,第三个环节——训练巩固,第四个环节——课堂小结,第五个环节——布置作业。
第一个环节:温故知新
教师出示表格,学生完成填空。
平行四边形定义:
平行四边形性质:分别从边、角、对角线方面引导学生回忆,请学生逐一回答,师生共同评价与补充。
平行四边形判定:分别从边与边、对角线相互关系方面引导学生回忆,请学生逐一回答,师生共同评价与补充。
教师用大屏幕展示一般平行四边形变成为矩形的变化图,让学生感受矩形与一般平行四边形的核心区别,增加对矩形的印象。
让一学生回忆矩形的定义,从矩形的边、角、对角线三个方面加以回忆矩形的性质与判定(用红色字体突出矩形的特殊性质,以引起学生有意注意,提高复习效率)。
让学生分别回忆菱形与正方形的定义、性质、判定(也用红色字体突出特殊性质)。
让学生以两人小组讨论平行四边形、矩形、菱形、正方形等的包含关系,用生活中的案例进行类比,让学生对他们的内涵加以理解,然后教师出示以下图片。
学生完成学案上的表格:
边 角 对角线
性质 判定 性质 判定 性质 判定
平行四边形
矩形
菱形
正方形
第二个环节:应用举例。
例1:顺次连接任意四边形各边的中点,所构成的四边形以下简称为“中点四边形”。试判断中点四边形EFGH的形状,并说明理由。
(1)添加一个条件,使四边形EFGH为菱形;
(2)添加一个条件,使四边形EFGH为矩形;
(3)添加一个条件,使四边形EFGH为正方形。
教师活动:教师先要求学生打开课本,反倒第77页,带领学生回忆“中点三角形”,分析中点三角形的特点,从而引出“中点四边形”的定义。
学生活动:学生两人一组探究中点四边形的性质,完成上述例题。
师生共同总结:
1顺次连接任意的四边形各边中点得平行四边形;
2顺次连接对角线相等的四边形各边中点得菱形;
3顺次连接对角线互相垂直的四边形各边中点得矩形;
4顺次连接对角线相等且互相垂直的四边形各边中点得正方形。
问题:那么,特殊平行四边形的“中点四边形”会是怎样的图形呢?
1.矩形的“中点四边形”是 形;
2.菱形的“中点四边形”是 形;
3.正方形的“中点四边形”是 形。
思考题:在矩形ABCD中,AB=16,BC=8.将矩形沿AC折叠,点D落在点E处,且CE交AB于点F,求AF的长。
点拨:对于折叠问题,可以从折叠前后的两个图形是全等图形入手进行分析,引导学生利用“双平”模型研究此类问题。
第三环节:训练巩固
1、检查一个门框是矩形的方法是( )
A、测量两条对角线是否相等.
B、测量有三个角是直角.
C、 测量两条对角线是否互相平分.
D、 测量两条对角线是否互相垂直.
2、顺次连接矩形各边中点所得的四边形是( )
A、矩形 B、菱形 C、梯形 D、正方形
思考题:如图,在□ABCD中,E、F、G、H分别是四条边上的点,且满足BE=DF,CG=AH,连接EF、GH。试说明:EF与GH互相平分。
第四个环节:课堂小结
通过本节课的复习,你取得了哪些经验?
活动目的:培养学生的语言组织能力、自我表现能力、综合能力,同时也检测了学生听课的认真程度,从学生的回答中了解不同程度的学生对这节课内容掌握的程度。
(
B
F
C
D
E
A
)第五个环节:布置作业
如图,已知AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F。
求证:①四边形AEDF是菱形
②连接EF,若AE=8,AD=12,求EF的长。
③当△ABC满足什么条件时,四边形AEDF是正方形?说明理由。
