19.2.2菱形(1) 课件
文档属性
| 名称 | 19.2.2菱形(1) 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 907.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-16 20:40:50 | ||
图片预览




文档简介
课件28张PPT。一起放飞理想的翅膀
在知识的天空中自由翱翔
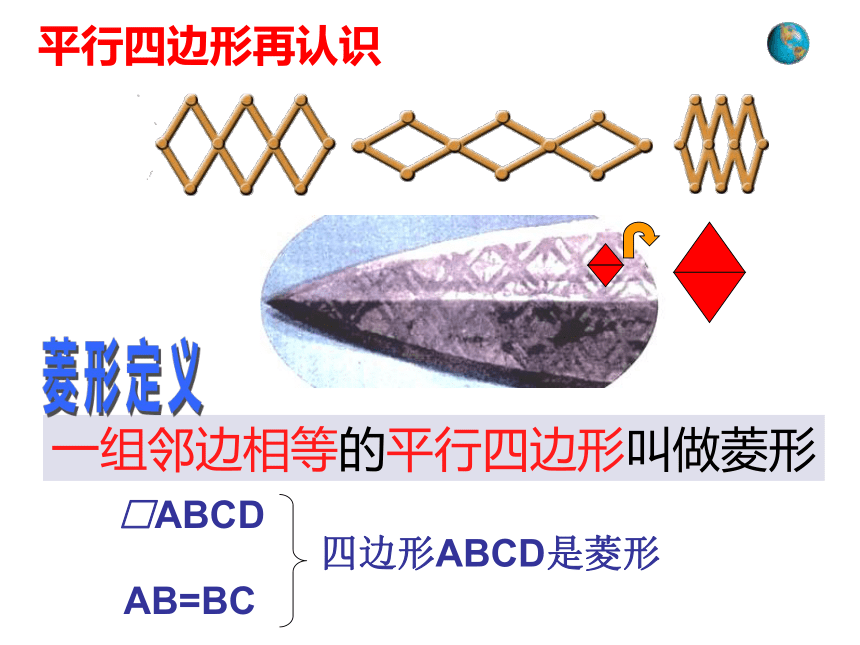
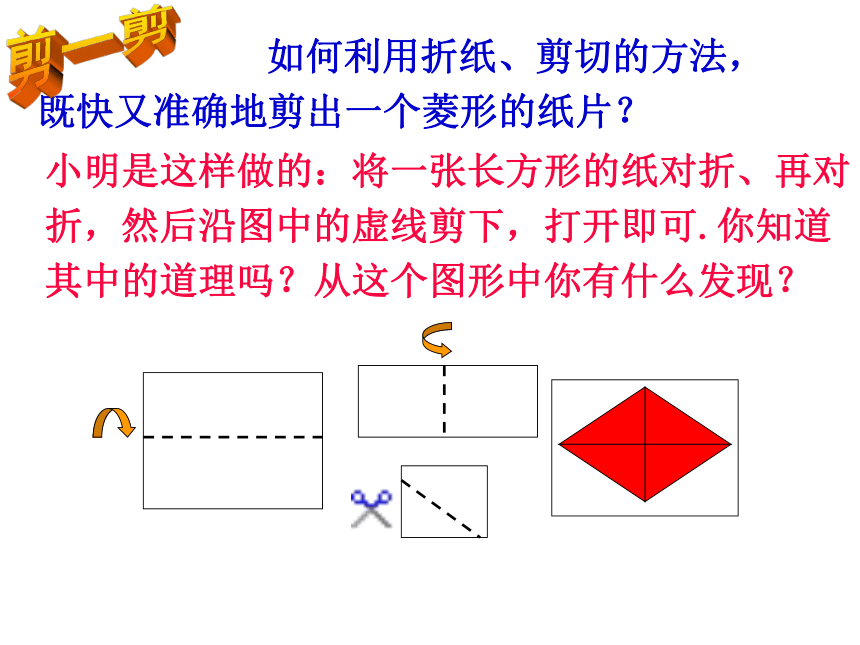
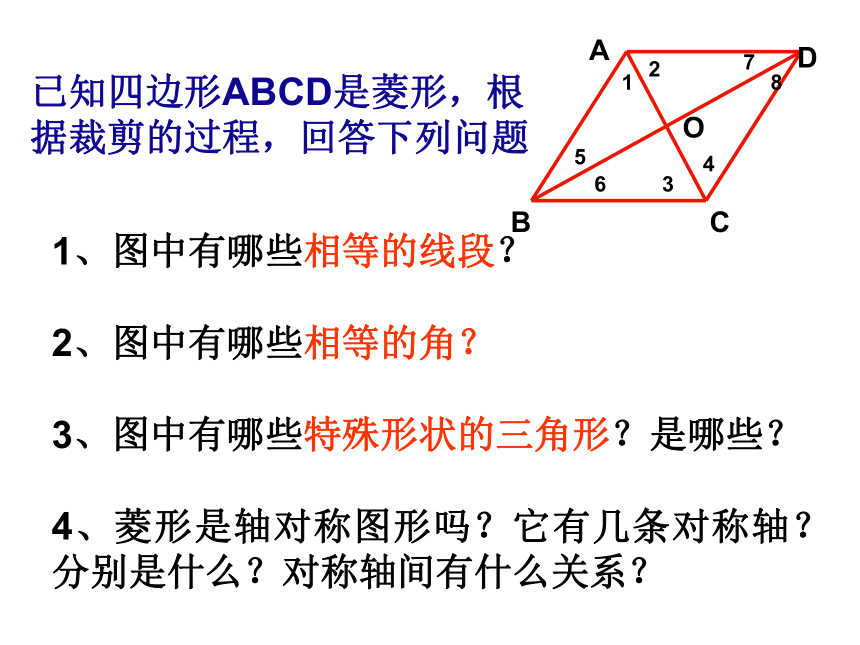
人教版数学教材八年级下19.2特殊的平行四边形19.2.2菱形的性质韩庄中学梁安全观 察下面的图形中有你熟悉的吗?三菱汽车标志欣赏 平行四边形再认识AB=BC四边形ABCD是菱形□ABCD小明是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗?从这个图形中你有什么发现? 如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?剪一剪已知四边形ABCD是菱形,根据裁剪的过程,回答下列问题ABCDO123456781、图中有哪些相等的线段?
2、图中有哪些相等的角?
3、图中有哪些特殊形状的三角形?是哪些?
4、菱形是轴对称图形吗?它有几条对称轴?分别是什么?对称轴间有什么关系?
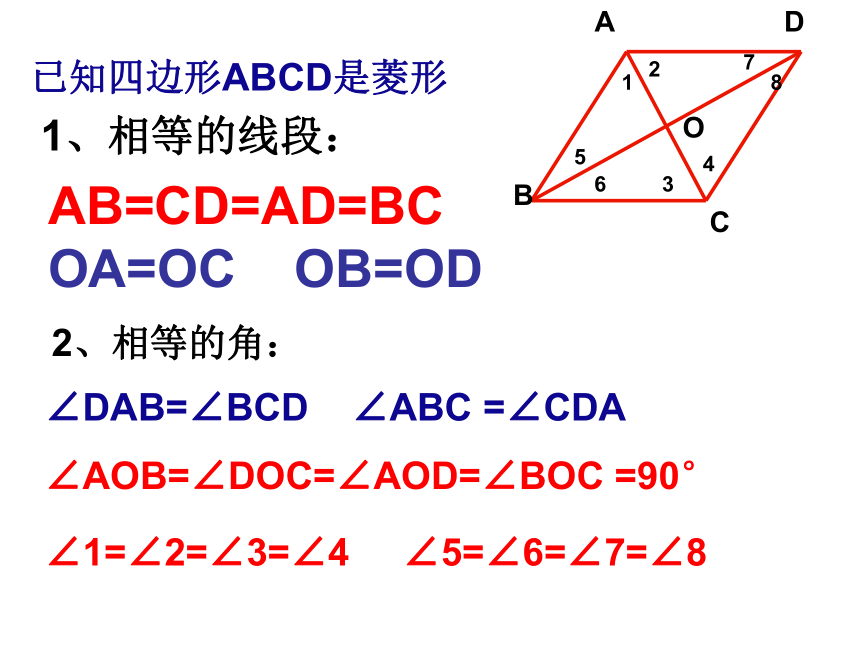
已知四边形ABCD是菱形ABCDO123456781、相等的线段:AB=CD=AD=BC
OA=OC OB=OD2、相等的角:∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
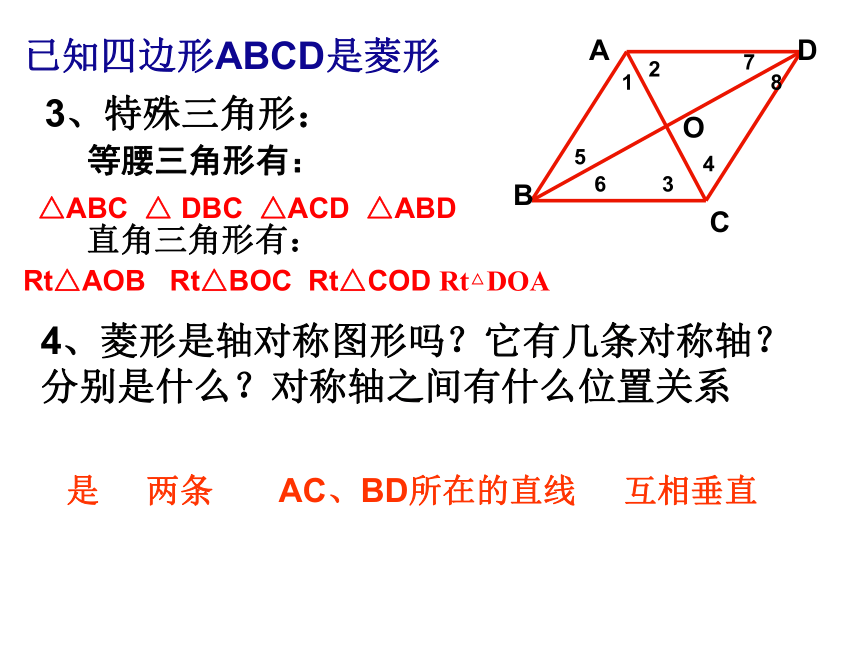
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8已知四边形ABCD是菱形ABCDO123456783、特殊三角形:△ABC △ DBC △ACD △ABD 直角三角形有:Rt△AOB Rt△BOC Rt△COD Rt△DOA
4、菱形是轴对称图形吗?它有几条对称轴?分别是什么?对称轴之间有什么位置关系是 两条 AC、BD所在的直线 互相垂直等腰三角形有:根据刚才的发现,猜想菱形具有哪些性质?(1)菱形具有平行四边形的一切性质;(2)菱形的四条边都相等;(3) 菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角;(4)菱形是轴对对称图形;也是中心对称图形; 命题: 菱形的四条边都相等。
已知:如图,四边ABCD是菱形
求证:AB=BC=CD=AD证明:∵四边形ABCD是菱形
∴ AB=CD AD=BC (平行四 边形的两组对边分别相等)
∵ AB=BC
∴ AB=BC=CD=ADABCD已知:在□ABCD中,AB=BC已知:菱形ABCD的对角线AC和BD相交于点O,如下图,证明:∵四边形ABCD是菱形∴ △ABD是等腰三角形
∵BO=DO∴AB=AD ,BO=DO∴AC⊥BD
AC平分∠BAD同理: AC平分∠BCD;
BD平分∠ABC和∠ADC
求证:AC⊥BD ;
AC平分∠BAD和∠BCD ;BD平分∠ABC和∠ADC 命题:菱形的对角线互相垂直平分,
并且每一条对角线平分一组对角;【菱形的面积公式】S菱形=BC× AE想一想:已知菱形的两条对角线的长,能求出它的面积吗? 菱形的面积=底×高=对角线乘积的一半菱形的 两条对角线互相平分菱形的对边平行边对角线角菱形的性质菱形的四条边相等菱形的对角相等菱形的邻角互补菱形的两条对角线互相垂直平分,每一条对角线平分一组对角。菱形的面积=底×高=对角线乘积的一半∵四边形ABCD是菱形,说说理由∴AD∥BC,AB∥CD ( )
AB=BC=CD=DA ( )OA=OC,OB=OD ( ) AC⊥BD ( )
∠ADB=∠CDB=∠ABD=∠CBD
= ∠ADC= ∠ABC ( )你都掌握了吗?
练一练学以致用1.已知菱形的周长是12cm,那么它的边长是______.2.菱形ABCD中∠ABC=60度,则∠BAC=_______。3cm60度3、菱形的两条对角线长分别为6cm和8cm,则菱形的边长是( )CA.10cm B.7cm C. 5cm D.4cm34有关菱形问题可转化为直角三角形或
等腰三角形的问题来解决 O解:∵ 花坛ABCD是菱形 ∴ AC⊥BD, ∠ABO = ∠ABC = ×60°=30° AB = BC = CD = AD = ×80 = 20 (m)在Rt△OAB中,AO= AB= ×20=10(m)BO= ≈17.32(m)∴ 花坛的两条小路长
AC = 2AO = 20 (m)
BD = 2BO ≈34.64(m) 花坛的面积 = AC·BD≈346.4 ( )4、已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AE=2。
求(1)∠ABC的度数;
(2)对角线AC、BD的长;
(3)菱形ABCD的面积。2∵四边形ABCD是菱形, ∴AD=AB解:∴AD=AB=BD∵ E是AB的中点,且DE⊥AB
∴DA=DB(DE为AB 的中垂线)∴ ∠DAB= 60 °, ∴ ∠ABC=120 °(2)∵AE=2, ∴ AB=4 ∴ BD=AB=4∵四边形ABCD是菱形,∴ AC⊥DB
∵ DB=4 ∴ 0B=2
∴ 在R t△AOB中,由勾股定理得 2AO=∴ AC=4(3)在Rt△DAE中,由勾股定理得 DE==2∴ S菱形ABCD=4×2(1)又AD=AB已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AE=2。
求(1)∠ABC的度数;
(2)对角线AC、BD的长;
(3)菱形ABCD的面积。OB= BD=2S菱形ABCD= AC×BD
=8 已知:如图,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F.
求证:EF⊥AD; 大显身手证明:∵ DE∥AC, DF∥AB
∴四边形AEDF是平行四边形
∵∠1=∠2,∠2= ∠3
∴ ∠1= ∠3
∴AE=DE
∴四边形AEDF是菱形(菱形的定义)
∴ EF⊥AD请你动脑筋把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?ACDB 在任意四边形ABCD中,对角线AC⊥BD ,且AC=18,BD=10。问四边形ABCD的面积是多少?试一试 =BD·AO+BD·CO =·BD· (AO+CO)=BD·AC =×10×18=90解:菱形性质的应用已知:如图,四边形ABCD是边长为13cm的菱形,其中对角线BD长10cm.求:(1).对角线AC的长度; (2).菱形的面积解:(1)∵四边形ABCD是菱形,=2×△ABD的面积∴∠AED=900,(2)菱形ABCD的面积=△ABD的面积+△CBD的面积∴AC=2AE=2×12=24(cm). 对自己说我有哪些收获? 对老师说你还有哪些困惑? 对同学有哪些温馨提示?畅所欲言知识再现1个定义2个公式3个特性:有一组邻边相等的平行四边形叫菱形:S菱形=底×高
S菱形= 对角线乘积的一半:特在“边、对角线、对称性”学而时习之,不亦说乎?教材:P102页第5题
P103页第11,12题 谢 谢
在知识的天空中自由翱翔
人教版数学教材八年级下19.2特殊的平行四边形19.2.2菱形的性质韩庄中学梁安全观 察下面的图形中有你熟悉的吗?三菱汽车标志欣赏 平行四边形再认识AB=BC四边形ABCD是菱形□ABCD小明是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗?从这个图形中你有什么发现? 如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?剪一剪已知四边形ABCD是菱形,根据裁剪的过程,回答下列问题ABCDO123456781、图中有哪些相等的线段?
2、图中有哪些相等的角?
3、图中有哪些特殊形状的三角形?是哪些?
4、菱形是轴对称图形吗?它有几条对称轴?分别是什么?对称轴间有什么关系?
已知四边形ABCD是菱形ABCDO123456781、相等的线段:AB=CD=AD=BC
OA=OC OB=OD2、相等的角:∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8已知四边形ABCD是菱形ABCDO123456783、特殊三角形:△ABC △ DBC △ACD △ABD 直角三角形有:Rt△AOB Rt△BOC Rt△COD Rt△DOA
4、菱形是轴对称图形吗?它有几条对称轴?分别是什么?对称轴之间有什么位置关系是 两条 AC、BD所在的直线 互相垂直等腰三角形有:根据刚才的发现,猜想菱形具有哪些性质?(1)菱形具有平行四边形的一切性质;(2)菱形的四条边都相等;(3) 菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角;(4)菱形是轴对对称图形;也是中心对称图形; 命题: 菱形的四条边都相等。
已知:如图,四边ABCD是菱形
求证:AB=BC=CD=AD证明:∵四边形ABCD是菱形
∴ AB=CD AD=BC (平行四 边形的两组对边分别相等)
∵ AB=BC
∴ AB=BC=CD=ADABCD已知:在□ABCD中,AB=BC已知:菱形ABCD的对角线AC和BD相交于点O,如下图,证明:∵四边形ABCD是菱形∴ △ABD是等腰三角形
∵BO=DO∴AB=AD ,BO=DO∴AC⊥BD
AC平分∠BAD同理: AC平分∠BCD;
BD平分∠ABC和∠ADC
求证:AC⊥BD ;
AC平分∠BAD和∠BCD ;BD平分∠ABC和∠ADC 命题:菱形的对角线互相垂直平分,
并且每一条对角线平分一组对角;【菱形的面积公式】S菱形=BC× AE想一想:已知菱形的两条对角线的长,能求出它的面积吗? 菱形的面积=底×高=对角线乘积的一半菱形的 两条对角线互相平分菱形的对边平行边对角线角菱形的性质菱形的四条边相等菱形的对角相等菱形的邻角互补菱形的两条对角线互相垂直平分,每一条对角线平分一组对角。菱形的面积=底×高=对角线乘积的一半∵四边形ABCD是菱形,说说理由∴AD∥BC,AB∥CD ( )
AB=BC=CD=DA ( )OA=OC,OB=OD ( ) AC⊥BD ( )
∠ADB=∠CDB=∠ABD=∠CBD
= ∠ADC= ∠ABC ( )你都掌握了吗?
练一练学以致用1.已知菱形的周长是12cm,那么它的边长是______.2.菱形ABCD中∠ABC=60度,则∠BAC=_______。3cm60度3、菱形的两条对角线长分别为6cm和8cm,则菱形的边长是( )CA.10cm B.7cm C. 5cm D.4cm34有关菱形问题可转化为直角三角形或
等腰三角形的问题来解决 O解:∵ 花坛ABCD是菱形 ∴ AC⊥BD, ∠ABO = ∠ABC = ×60°=30° AB = BC = CD = AD = ×80 = 20 (m)在Rt△OAB中,AO= AB= ×20=10(m)BO= ≈17.32(m)∴ 花坛的两条小路长
AC = 2AO = 20 (m)
BD = 2BO ≈34.64(m) 花坛的面积 = AC·BD≈346.4 ( )4、已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AE=2。
求(1)∠ABC的度数;
(2)对角线AC、BD的长;
(3)菱形ABCD的面积。2∵四边形ABCD是菱形, ∴AD=AB解:∴AD=AB=BD∵ E是AB的中点,且DE⊥AB
∴DA=DB(DE为AB 的中垂线)∴ ∠DAB= 60 °, ∴ ∠ABC=120 °(2)∵AE=2, ∴ AB=4 ∴ BD=AB=4∵四边形ABCD是菱形,∴ AC⊥DB
∵ DB=4 ∴ 0B=2
∴ 在R t△AOB中,由勾股定理得 2AO=∴ AC=4(3)在Rt△DAE中,由勾股定理得 DE==2∴ S菱形ABCD=4×2(1)又AD=AB已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AE=2。
求(1)∠ABC的度数;
(2)对角线AC、BD的长;
(3)菱形ABCD的面积。OB= BD=2S菱形ABCD= AC×BD
=8 已知:如图,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F.
求证:EF⊥AD; 大显身手证明:∵ DE∥AC, DF∥AB
∴四边形AEDF是平行四边形
∵∠1=∠2,∠2= ∠3
∴ ∠1= ∠3
∴AE=DE
∴四边形AEDF是菱形(菱形的定义)
∴ EF⊥AD请你动脑筋把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?ACDB 在任意四边形ABCD中,对角线AC⊥BD ,且AC=18,BD=10。问四边形ABCD的面积是多少?试一试 =BD·AO+BD·CO =·BD· (AO+CO)=BD·AC =×10×18=90解:菱形性质的应用已知:如图,四边形ABCD是边长为13cm的菱形,其中对角线BD长10cm.求:(1).对角线AC的长度; (2).菱形的面积解:(1)∵四边形ABCD是菱形,=2×△ABD的面积∴∠AED=900,(2)菱形ABCD的面积=△ABD的面积+△CBD的面积∴AC=2AE=2×12=24(cm). 对自己说我有哪些收获? 对老师说你还有哪些困惑? 对同学有哪些温馨提示?畅所欲言知识再现1个定义2个公式3个特性:有一组邻边相等的平行四边形叫菱形:S菱形=底×高
S菱形= 对角线乘积的一半:特在“边、对角线、对称性”学而时习之,不亦说乎?教材:P102页第5题
P103页第11,12题 谢 谢
