第5讲 数列与不等式(2022年高考真题分类汇编)(解析版)
文档属性
| 名称 | 第5讲 数列与不等式(2022年高考真题分类汇编)(解析版) | 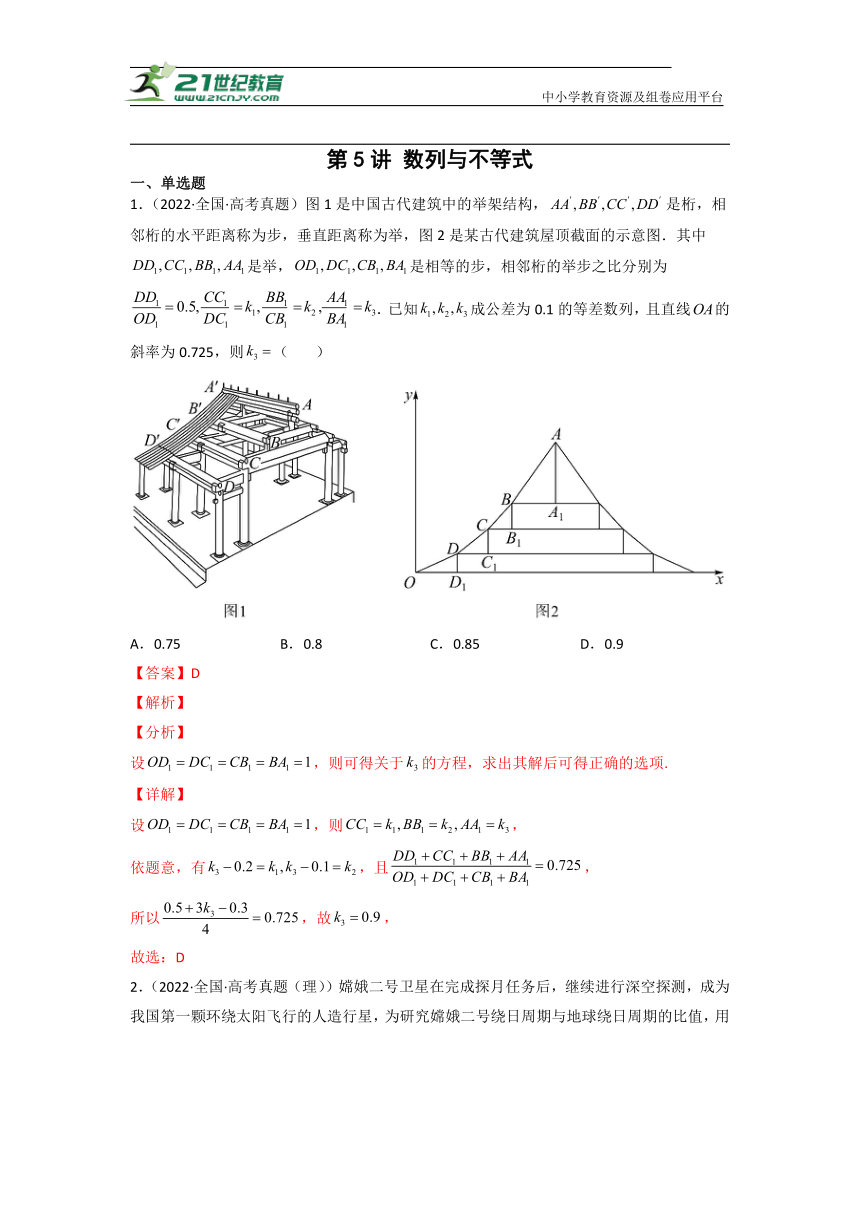 | |
| 格式 | docx | ||
| 文件大小 | 542.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-13 09:59:48 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第5讲 数列与不等式
一、单选题
1.(2022·全国·高考真题)图1是中国古代建筑中的举架结构,是桁,相邻桁的水平距离称为步,垂直距离称为举,图2是某古代建筑屋顶截面的示意图.其中是举,是相等的步,相邻桁的举步之比分别为.已知成公差为0.1的等差数列,且直线的斜率为0.725,则( )
A.0.75 B.0.8 C.0.85 D.0.9
【答案】D
【解析】
【分析】
设,则可得关于的方程,求出其解后可得正确的选项.
【详解】
设,则,
依题意,有,且,
所以,故,
故选:D
2.(2022·全国·高考真题(理))嫦娥二号卫星在完成探月任务后,继续进行深空探测,成为我国第一颗环绕太阳飞行的人造行星,为研究嫦娥二号绕日周期与地球绕日周期的比值,用到数列:,,,…,依此类推,其中.则( )
A. B. C. D.
【答案】D
【解析】
【分析】
根据,再利用数列与的关系判断中各项的大小,即可求解.
【详解】
解:因为,
所以,,得到,
同理,可得,
又因为,
故,;
以此类推,可得,,故A错误;
,故B错误;
,得,故C错误;
,得,故D正确.
故选:D.
3.(2022·全国·高考真题(文))已知等比数列的前3项和为168,,则( )
A.14 B.12 C.6 D.3
【答案】D
【解析】
【分析】
设等比数列的公比为,易得,根据题意求出首项与公比,再根据等比数列的通项即可得解.
【详解】
解:设等比数列的公比为,
若,则,与题意矛盾,
所以,
则,解得,
所以.
故选:D.
二、填空题
4.(2022·全国·高考真题(文))记为等差数列的前n项和.若,则公差_______.
【答案】2
【解析】
【分析】
转化条件为,即可得解.
【详解】
由可得,化简得,
即,解得.
故答案为:2.
三、解答题
5.(2022·全国·高考真题)已知为等差数列,是公比为2的等比数列,且.
(1)证明:;
(2)求集合中元素个数.
【答案】(1)证明见解析;
(2).
【解析】
【分析】
(1)设数列的公差为,根据题意列出方程组即可证出;
(2)根据题意化简可得,即可解出.
(1)
设数列的公差为,所以,,即可解得,,所以原命题得证.
(2)
由(1)知,,所以,即,亦即,解得,所以满足等式的解,故集合中的元素个数为.
6.(2022·全国·高考真题)记为数列的前n项和,已知是公差为的等差数列.
(1)求的通项公式;
(2)证明:.
【答案】(1)
(2)见解析
【解析】
【分析】
(1)利用等差数列的通项公式求得,得到,利用和与项的关系得到当时,,进而得:,利用累乘法求得,检验对于也成立,得到的通项公式;
(2)由(1)的结论,利用裂项求和法得到,进而证得.
(1)
∵,∴,∴,
又∵是公差为的等差数列,
∴,∴,
∴当时,,
∴,
整理得:,
即,
∴
,
显然对于也成立,
∴的通项公式;
(2)
∴
7.(2022·全国·高考真题(理))记为数列的前n项和.已知.
(1)证明:是等差数列;
(2)若成等比数列,求的最小值.
【答案】(1)证明见解析;
(2).
【解析】
【分析】
(1)依题意可得,根据,作差即可得到,从而得证;
(2)由(1)及等比中项的性质求出,即可得到的通项公式与前项和,再根据二次函数的性质计算可得.
(1)
解:因为,即①,
当时,②,
①②得,,
即,
即,所以,且,
所以是以为公差的等差数列.
(2)
解:由(1)可得,,,
又,,成等比数列,所以,
即,解得,
所以,所以,
所以,当或时.
第5讲 数列与不等式
一、单选题
1.(2022·全国·高考真题)图1是中国古代建筑中的举架结构,是桁,相邻桁的水平距离称为步,垂直距离称为举,图2是某古代建筑屋顶截面的示意图.其中是举,是相等的步,相邻桁的举步之比分别为.已知成公差为0.1的等差数列,且直线的斜率为0.725,则( )
A.0.75 B.0.8 C.0.85 D.0.9
【答案】D
【解析】
【分析】
设,则可得关于的方程,求出其解后可得正确的选项.
【详解】
设,则,
依题意,有,且,
所以,故,
故选:D
2.(2022·全国·高考真题(理))嫦娥二号卫星在完成探月任务后,继续进行深空探测,成为我国第一颗环绕太阳飞行的人造行星,为研究嫦娥二号绕日周期与地球绕日周期的比值,用到数列:,,,…,依此类推,其中.则( )
A. B. C. D.
【答案】D
【解析】
【分析】
根据,再利用数列与的关系判断中各项的大小,即可求解.
【详解】
解:因为,
所以,,得到,
同理,可得,
又因为,
故,;
以此类推,可得,,故A错误;
,故B错误;
,得,故C错误;
,得,故D正确.
故选:D.
3.(2022·全国·高考真题(文))已知等比数列的前3项和为168,,则( )
A.14 B.12 C.6 D.3
【答案】D
【解析】
【分析】
设等比数列的公比为,易得,根据题意求出首项与公比,再根据等比数列的通项即可得解.
【详解】
解:设等比数列的公比为,
若,则,与题意矛盾,
所以,
则,解得,
所以.
故选:D.
二、填空题
4.(2022·全国·高考真题(文))记为等差数列的前n项和.若,则公差_______.
【答案】2
【解析】
【分析】
转化条件为,即可得解.
【详解】
由可得,化简得,
即,解得.
故答案为:2.
三、解答题
5.(2022·全国·高考真题)已知为等差数列,是公比为2的等比数列,且.
(1)证明:;
(2)求集合中元素个数.
【答案】(1)证明见解析;
(2).
【解析】
【分析】
(1)设数列的公差为,根据题意列出方程组即可证出;
(2)根据题意化简可得,即可解出.
(1)
设数列的公差为,所以,,即可解得,,所以原命题得证.
(2)
由(1)知,,所以,即,亦即,解得,所以满足等式的解,故集合中的元素个数为.
6.(2022·全国·高考真题)记为数列的前n项和,已知是公差为的等差数列.
(1)求的通项公式;
(2)证明:.
【答案】(1)
(2)见解析
【解析】
【分析】
(1)利用等差数列的通项公式求得,得到,利用和与项的关系得到当时,,进而得:,利用累乘法求得,检验对于也成立,得到的通项公式;
(2)由(1)的结论,利用裂项求和法得到,进而证得.
(1)
∵,∴,∴,
又∵是公差为的等差数列,
∴,∴,
∴当时,,
∴,
整理得:,
即,
∴
,
显然对于也成立,
∴的通项公式;
(2)
∴
7.(2022·全国·高考真题(理))记为数列的前n项和.已知.
(1)证明:是等差数列;
(2)若成等比数列,求的最小值.
【答案】(1)证明见解析;
(2).
【解析】
【分析】
(1)依题意可得,根据,作差即可得到,从而得证;
(2)由(1)及等比中项的性质求出,即可得到的通项公式与前项和,再根据二次函数的性质计算可得.
(1)
解:因为,即①,
当时,②,
①②得,,
即,
即,所以,且,
所以是以为公差的等差数列.
(2)
解:由(1)可得,,,
又,,成等比数列,所以,
即,解得,
所以,所以,
所以,当或时.
同课章节目录
