沪科版数学八年级下册 18.1 勾股定理教案
文档属性
| 名称 | 沪科版数学八年级下册 18.1 勾股定理教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 41.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-13 15:19:58 | ||
图片预览

文档简介
18.1勾股定理
一、教材分析 :
勾股定理是直角三角形的一条非常重要的性质,它将数与形密切地联系起来,揭示了一个直角三角形三边之间的数量关系,是后续学习解直角三角形的基础,是三角形知识的深化。
二、教学目标:
(1)知识与技能:理解割补法求解图形面积的方法.了解勾股定理的产生背景,体验勾股定理的探索过程,掌握验证勾股定理的方法与证明过程.
(2)过程与方法:通过经历观察、猜想、归纳、证明的探究过程,让学生体会数形结合的方法,掌握特殊到一般的数学规律
(3)情感、态度与价值观:通过经历对勾股定理的探究过程,培养学生归纳问题的能力,同时教学过程中穿插我国科学家对勾股定理的研究,激发学生的爱国情感。
三、教学重、难点:
重点:探索和证明勾股定理
难点:1.割补法求解图形的面积.
2.等积法描述图形的面积
3.勾股定理的证明
教学方法:
讲授法、启发式教学、小组讨论
五、教学准备:
自制课件、田字格纸、以裁剪好的全等的直角三角形、实物展台
六、教学过程:
一、创设情境,导入新课
1、提问:我国近代最著名的数学家是谁 同学们知不知道 展示华罗庚与冯康的图片,告诉学生华罗庚与冯康在数学上都取得了很多伟大的成就,但是这些结果的取得都是从很简单的知识开始学习的。
二、探究割补法求面积的方法
师:如何在不知道正方形边长的基础上求解正方形面积(PPT展示图片,边长为1,正方形的四个顶点落在格点上)
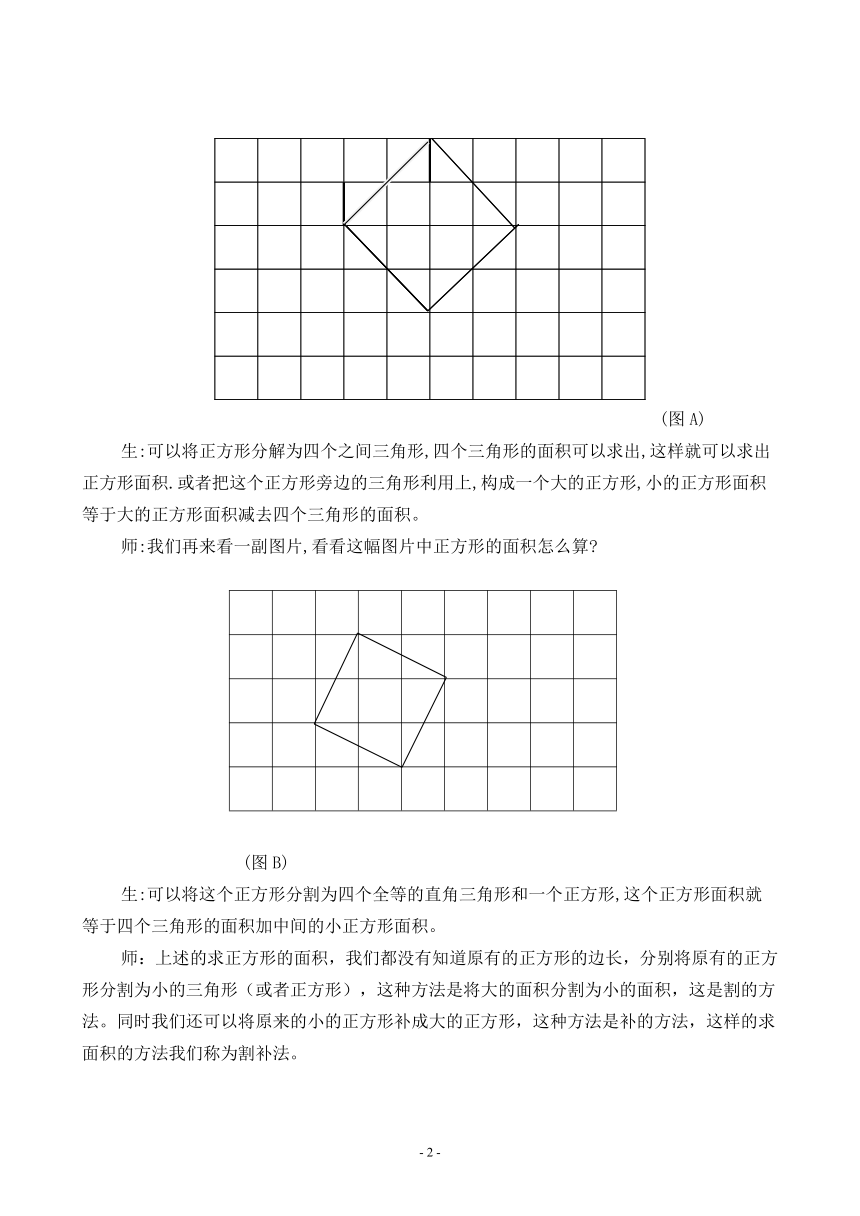
(图A)
生:可以将正方形分解为四个之间三角形,四个三角形的面积可以求出,这样就可以求出正方形面积.或者把这个正方形旁边的三角形利用上,构成一个大的正方形,小的正方形面积等于大的正方形面积减去四个三角形的面积。
师:我们再来看一副图片,看看这幅图片中正方形的面积怎么算
(图B)
生:可以将这个正方形分割为四个全等的直角三角形和一个正方形,这个正方形面积就等于四个三角形的面积加中间的小正方形面积。
师:上述的求正方形的面积,我们都没有知道原有的正方形的边长,分别将原有的正方形分割为小的三角形(或者正方形),这种方法是将大的面积分割为小的面积,这是割的方法。同时我们还可以将原来的小的正方形补成大的正方形,这种方法是补的方法,这样的求面积的方法我们称为割补法。
三、探究勾股定理的表达式
1、探究直角三角形的三边之间的特殊关系
(
1
2
3
、
)(1)展示图片:(如图是一个行距、列距都是1的方格网。在方格网中投影显示出以格点为顶点等腰直角,并显示分别以三角形的各边为边,向形外作正方形1、2、3。)
提出问题:三个正方形S1,S2,S3面积分别是多少?它们之间有怎样的关系?学生观察图片,分组交流.
老师在黑板画出表格进行记录,请一组同学回答S1,S2,S3面积,老师填入表格
图1 图2 图3 图4 图5
S1
S2
S3
(
、
1
2
3
)2、探究一般直角三角形的三边之间的特殊关系
(1)展示图片(在行距、列距都是1的方格网中,再作一个格点不等腰直角、,分别以三角形的各边为边,向形外作正方形1、2、3。)让学生在课前备好的网格纸上画图,然后投影出图。
引导思考:1、三个正方形面积S1、S2和S3分别是多少?S1、S2和S3分别是多少(学生分组交流)。老师请学生回答填入表格。
3、学生探究一般直角三角形的三边之间的特殊关系
各个小组根据老师发放的田字格纸,先画出任意的直角三角形,再以直角三角形的三边为边长画出正方形,以两直角边为边长的正方形的面积为S1、S2,以斜边为边长的正方形面积为S3,小组讨论并作图。
学生根据问题,分组交流:
分别请三组不同的同学上台展示作图的效果(实物展台)老师将结果填入图表
引导学生思考:你们发现S1,S2,S3满足什么关系?你们发现直角三角形三边的长有怎样的关系?能用简练的语言概括出来吗?
学生回答,并归纳总结:直角三角形两条直角边的平方和,等于斜边的平方。
四、证明勾股定理
师:我们刚刚得到一个结论:直角三角形两条直角边的平方和,等于斜边的平方。这个结论是我们通过同学们做的直角三角形得出来的,是不是一个定理。
生:我们得到的只是一个猜想,要对于所有的直角三角形都成立,必须证明它是正确的。
2、引导学生将猜想转化为数学语言:如图在直角△ABC中,∠C=90°AB=C,BC=a, AC=b,
(
c
a
b
)求证:a2+b2=c2
3、向学生发放四个全等的直角三角形,拼为一个正方形,并思考正方形的面积可以怎么表示(假设较短的直角边为a,较长的直角边为b,斜边为c),老师巡视,并请学生板演(利用磁铁)
方法一:如图所示将四个直角三角形拼成正方形(学生上台拼接和板演)
S正方形=c2+4*1/2*ab=(a+b)2
即:c2= a2+ b2
方法二::将四个全等的直角三角形拼成如图所示的正方形,
七、课堂小结:
1、通过这节课的学习,你有哪些收获?
2、学了这节课有什么感想?
八、布置作业:
课后作业习题18.1 1
九、教材反思:
- 5 -
一、教材分析 :
勾股定理是直角三角形的一条非常重要的性质,它将数与形密切地联系起来,揭示了一个直角三角形三边之间的数量关系,是后续学习解直角三角形的基础,是三角形知识的深化。
二、教学目标:
(1)知识与技能:理解割补法求解图形面积的方法.了解勾股定理的产生背景,体验勾股定理的探索过程,掌握验证勾股定理的方法与证明过程.
(2)过程与方法:通过经历观察、猜想、归纳、证明的探究过程,让学生体会数形结合的方法,掌握特殊到一般的数学规律
(3)情感、态度与价值观:通过经历对勾股定理的探究过程,培养学生归纳问题的能力,同时教学过程中穿插我国科学家对勾股定理的研究,激发学生的爱国情感。
三、教学重、难点:
重点:探索和证明勾股定理
难点:1.割补法求解图形的面积.
2.等积法描述图形的面积
3.勾股定理的证明
教学方法:
讲授法、启发式教学、小组讨论
五、教学准备:
自制课件、田字格纸、以裁剪好的全等的直角三角形、实物展台
六、教学过程:
一、创设情境,导入新课
1、提问:我国近代最著名的数学家是谁 同学们知不知道 展示华罗庚与冯康的图片,告诉学生华罗庚与冯康在数学上都取得了很多伟大的成就,但是这些结果的取得都是从很简单的知识开始学习的。
二、探究割补法求面积的方法
师:如何在不知道正方形边长的基础上求解正方形面积(PPT展示图片,边长为1,正方形的四个顶点落在格点上)
(图A)
生:可以将正方形分解为四个之间三角形,四个三角形的面积可以求出,这样就可以求出正方形面积.或者把这个正方形旁边的三角形利用上,构成一个大的正方形,小的正方形面积等于大的正方形面积减去四个三角形的面积。
师:我们再来看一副图片,看看这幅图片中正方形的面积怎么算
(图B)
生:可以将这个正方形分割为四个全等的直角三角形和一个正方形,这个正方形面积就等于四个三角形的面积加中间的小正方形面积。
师:上述的求正方形的面积,我们都没有知道原有的正方形的边长,分别将原有的正方形分割为小的三角形(或者正方形),这种方法是将大的面积分割为小的面积,这是割的方法。同时我们还可以将原来的小的正方形补成大的正方形,这种方法是补的方法,这样的求面积的方法我们称为割补法。
三、探究勾股定理的表达式
1、探究直角三角形的三边之间的特殊关系
(
1
2
3
、
)(1)展示图片:(如图是一个行距、列距都是1的方格网。在方格网中投影显示出以格点为顶点等腰直角,并显示分别以三角形的各边为边,向形外作正方形1、2、3。)
提出问题:三个正方形S1,S2,S3面积分别是多少?它们之间有怎样的关系?学生观察图片,分组交流.
老师在黑板画出表格进行记录,请一组同学回答S1,S2,S3面积,老师填入表格
图1 图2 图3 图4 图5
S1
S2
S3
(
、
1
2
3
)2、探究一般直角三角形的三边之间的特殊关系
(1)展示图片(在行距、列距都是1的方格网中,再作一个格点不等腰直角、,分别以三角形的各边为边,向形外作正方形1、2、3。)让学生在课前备好的网格纸上画图,然后投影出图。
引导思考:1、三个正方形面积S1、S2和S3分别是多少?S1、S2和S3分别是多少(学生分组交流)。老师请学生回答填入表格。
3、学生探究一般直角三角形的三边之间的特殊关系
各个小组根据老师发放的田字格纸,先画出任意的直角三角形,再以直角三角形的三边为边长画出正方形,以两直角边为边长的正方形的面积为S1、S2,以斜边为边长的正方形面积为S3,小组讨论并作图。
学生根据问题,分组交流:
分别请三组不同的同学上台展示作图的效果(实物展台)老师将结果填入图表
引导学生思考:你们发现S1,S2,S3满足什么关系?你们发现直角三角形三边的长有怎样的关系?能用简练的语言概括出来吗?
学生回答,并归纳总结:直角三角形两条直角边的平方和,等于斜边的平方。
四、证明勾股定理
师:我们刚刚得到一个结论:直角三角形两条直角边的平方和,等于斜边的平方。这个结论是我们通过同学们做的直角三角形得出来的,是不是一个定理。
生:我们得到的只是一个猜想,要对于所有的直角三角形都成立,必须证明它是正确的。
2、引导学生将猜想转化为数学语言:如图在直角△ABC中,∠C=90°AB=C,BC=a, AC=b,
(
c
a
b
)求证:a2+b2=c2
3、向学生发放四个全等的直角三角形,拼为一个正方形,并思考正方形的面积可以怎么表示(假设较短的直角边为a,较长的直角边为b,斜边为c),老师巡视,并请学生板演(利用磁铁)
方法一:如图所示将四个直角三角形拼成正方形(学生上台拼接和板演)
S正方形=c2+4*1/2*ab=(a+b)2
即:c2= a2+ b2
方法二::将四个全等的直角三角形拼成如图所示的正方形,
七、课堂小结:
1、通过这节课的学习,你有哪些收获?
2、学了这节课有什么感想?
八、布置作业:
课后作业习题18.1 1
九、教材反思:
- 5 -
