北京版九年级数学上册第21章 《圆的复习—求圆中的弦长》教学设计(表格式)
文档属性
| 名称 | 北京版九年级数学上册第21章 《圆的复习—求圆中的弦长》教学设计(表格式) |

|
|
| 格式 | doc | ||
| 文件大小 | 253.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-13 00:00:00 | ||
图片预览

文档简介
圆的复习—求圆中的弦长
学情分析
【学情分析】1.知识能力:学生已经学习了解直角三角形,等腰三角形,圆等相关知识 2.数学能力:能完成简单问题的计算证明,对于复杂问题,复杂图形有困难 3.学生读题和读图的能力差别很大,缺乏逻辑推理能力,对于复杂问题,复杂图形有困难.
教学目标分析
1.探索把15o,22.5o,30o,60o的角,转化到直角或者等边三角形中解决问题,学会分析题中的有用信息.2.经历角的转化,解斜三角形通过做垂线转化为解直角三角形,发展学生合情推理和逻辑思维能力3.培养学生分析、解决复杂问题的能力 ,感受转化思想的应用.
中考要求
A级 了解弧、弦、圆心角的关系;理解弧、弦、圆心角与圆周角及其所对弧之间的关系B 级 能利用垂径定理解决有关简单问题;能利用圆周角定理及其推论解决有关简单问题;能利用锐角三角函数的有关知识解直角三角形;能利用锐角三角函数的有关知识解决一些简单的实用问题C级 运用圆的性质的有关内容解决有关问题
教学重难点分析
教学重点:角的转化和圆中的基本计算教学难点:如何构造含特殊角的直角三角形
教学过程
教学环节
活动一 课前小测 教师活动巡视学生作答情况 学生活动思考作答 设计意图帮助学生复习基础知识
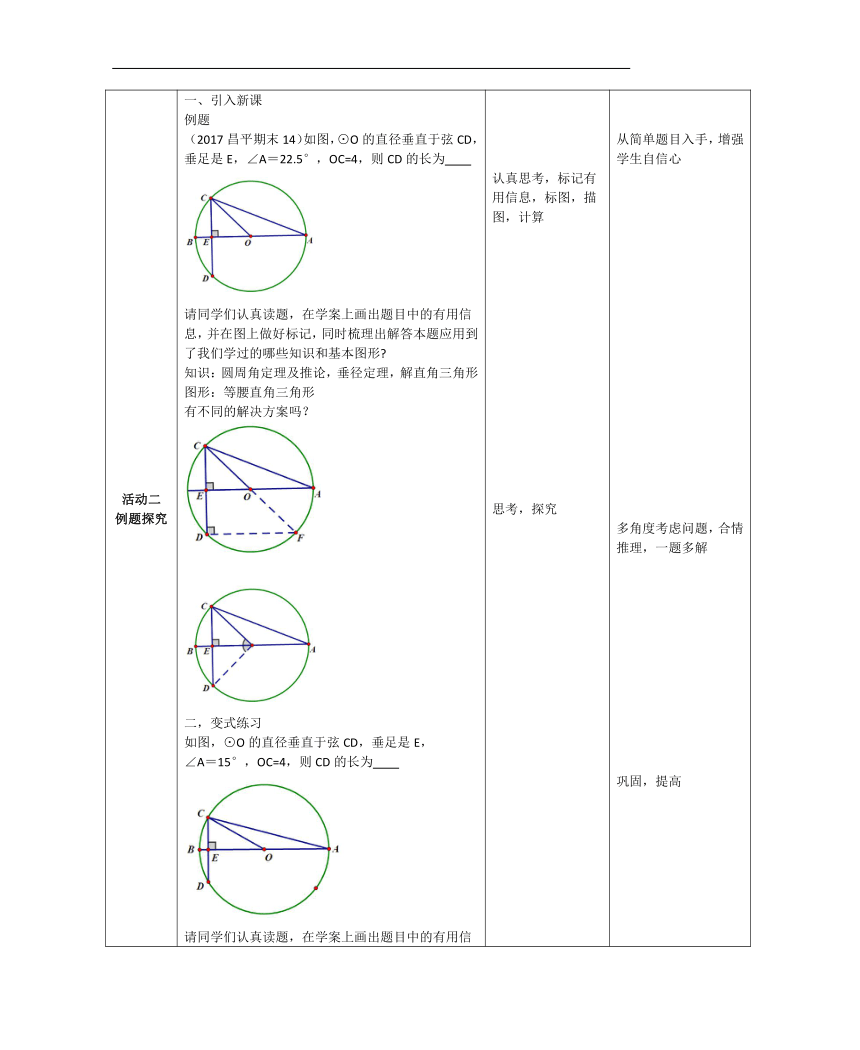
活动二例题探究 引入新课例题(2017昌平期末14)如图,⊙O的直径垂直于弦CD,垂足是E,∠A=22.5°,OC=4,则CD的长为 请同学们认真读题,在学案上画出题目中的有用信息,并在图上做好标记,同时梳理出解答本题应用到了我们学过的哪些知识和基本图形 知识:圆周角定理及推论,垂径定理,解直角三角形图形:等腰直角三角形有不同的解决方案吗?二,变式练习如图,⊙O的直径垂直于弦CD,垂足是E,∠A=15°,OC=4,则CD的长为 请同学们认真读题,在学案上画出题目中的有用信息,并在图上做好标记,同时梳理出解答本题应用到了我们学过的哪些知识和基本图形 知识:圆周角定理及推论,垂径定理,解直角三角形图形:含有30°角的直角三角形,等边三角形归纳小结1.知识:圆周角定理及推论(角的关系) 垂径定理(线等.弦等.角等) 解直角三角形(边角关系)2.图形: 3.辅助线: 连半径--等腰三角形 够直径--直角三角形 认真思考,标记有用信息,标图,描图,计算思考,探究思考归纳,合作交流,总结共性仔细阅读,标图,描图,找出图中的关键信息思考作答 从简单题目入手,增强学生自信心多角度考虑问题,合情推理,一题多解巩固,提高类比,归纳总结归纳,培养总结,反思的习惯
活动三巩固提高 三.巩固提高1.(2017昌平期末,21).如图,△ABC内接于⊙O, 若⊙O的半径为6,∠B=60°,求AC的长.2.(2017西城期末25).如图,△ABC内接于⊙O,直径DE⊥AB于点F,交BC于点 M,DE的延长线与AC的延长线交于点N,连接AM. (1)求证:AM=BM;(2)若AM⊥BM,DE=8,∠N=15°,求BC的长. 仔细阅读,标图,描图,找出图中的关键信息,分离出第一问标图,描图,运用转化思想,合情推理出其他有用信息,并在图中标出思考,作答分组讨论类比归纳 巩固提升,体会转化思想的实际应用感受分离图形,化繁为简的作用进一步培养学生从复杂图形中分离出基本图形,排除干扰信息的能力逻辑推理能力
四小结 总结一下本节课你的收获1.知识:圆周角定理及推论(角的关系) 垂径定理(线等.弦等.角等) 解直角三角形(边角关系)2.图形: 3.辅助线: 连半径--等腰三角形 够直径--直角三角形4.分离图形,转化 学生和老师共同总结本课所学知识和解题方法 对学习的重点再次巩固
五作业 (2017西城期末23).如图,AB是⊙O的直径,C为⊙O上一点,经过点C的直线与AB的延长线交于点D,连接AC,BC,∠BCD =∠CAB.E是⊙O上一点,弧CB=弧CE,连接AE并延长与DC的延长线交于点F.(1)求证:DC是⊙O的切线; (2)若⊙O的半径为3, sinD=,求线段AF的长 拓展,强化,为下面的复习做好准备
学情分析
【学情分析】1.知识能力:学生已经学习了解直角三角形,等腰三角形,圆等相关知识 2.数学能力:能完成简单问题的计算证明,对于复杂问题,复杂图形有困难 3.学生读题和读图的能力差别很大,缺乏逻辑推理能力,对于复杂问题,复杂图形有困难.
教学目标分析
1.探索把15o,22.5o,30o,60o的角,转化到直角或者等边三角形中解决问题,学会分析题中的有用信息.2.经历角的转化,解斜三角形通过做垂线转化为解直角三角形,发展学生合情推理和逻辑思维能力3.培养学生分析、解决复杂问题的能力 ,感受转化思想的应用.
中考要求
A级 了解弧、弦、圆心角的关系;理解弧、弦、圆心角与圆周角及其所对弧之间的关系B 级 能利用垂径定理解决有关简单问题;能利用圆周角定理及其推论解决有关简单问题;能利用锐角三角函数的有关知识解直角三角形;能利用锐角三角函数的有关知识解决一些简单的实用问题C级 运用圆的性质的有关内容解决有关问题
教学重难点分析
教学重点:角的转化和圆中的基本计算教学难点:如何构造含特殊角的直角三角形
教学过程
教学环节
活动一 课前小测 教师活动巡视学生作答情况 学生活动思考作答 设计意图帮助学生复习基础知识
活动二例题探究 引入新课例题(2017昌平期末14)如图,⊙O的直径垂直于弦CD,垂足是E,∠A=22.5°,OC=4,则CD的长为 请同学们认真读题,在学案上画出题目中的有用信息,并在图上做好标记,同时梳理出解答本题应用到了我们学过的哪些知识和基本图形 知识:圆周角定理及推论,垂径定理,解直角三角形图形:等腰直角三角形有不同的解决方案吗?二,变式练习如图,⊙O的直径垂直于弦CD,垂足是E,∠A=15°,OC=4,则CD的长为 请同学们认真读题,在学案上画出题目中的有用信息,并在图上做好标记,同时梳理出解答本题应用到了我们学过的哪些知识和基本图形 知识:圆周角定理及推论,垂径定理,解直角三角形图形:含有30°角的直角三角形,等边三角形归纳小结1.知识:圆周角定理及推论(角的关系) 垂径定理(线等.弦等.角等) 解直角三角形(边角关系)2.图形: 3.辅助线: 连半径--等腰三角形 够直径--直角三角形 认真思考,标记有用信息,标图,描图,计算思考,探究思考归纳,合作交流,总结共性仔细阅读,标图,描图,找出图中的关键信息思考作答 从简单题目入手,增强学生自信心多角度考虑问题,合情推理,一题多解巩固,提高类比,归纳总结归纳,培养总结,反思的习惯
活动三巩固提高 三.巩固提高1.(2017昌平期末,21).如图,△ABC内接于⊙O, 若⊙O的半径为6,∠B=60°,求AC的长.2.(2017西城期末25).如图,△ABC内接于⊙O,直径DE⊥AB于点F,交BC于点 M,DE的延长线与AC的延长线交于点N,连接AM. (1)求证:AM=BM;(2)若AM⊥BM,DE=8,∠N=15°,求BC的长. 仔细阅读,标图,描图,找出图中的关键信息,分离出第一问标图,描图,运用转化思想,合情推理出其他有用信息,并在图中标出思考,作答分组讨论类比归纳 巩固提升,体会转化思想的实际应用感受分离图形,化繁为简的作用进一步培养学生从复杂图形中分离出基本图形,排除干扰信息的能力逻辑推理能力
四小结 总结一下本节课你的收获1.知识:圆周角定理及推论(角的关系) 垂径定理(线等.弦等.角等) 解直角三角形(边角关系)2.图形: 3.辅助线: 连半径--等腰三角形 够直径--直角三角形4.分离图形,转化 学生和老师共同总结本课所学知识和解题方法 对学习的重点再次巩固
五作业 (2017西城期末23).如图,AB是⊙O的直径,C为⊙O上一点,经过点C的直线与AB的延长线交于点D,连接AC,BC,∠BCD =∠CAB.E是⊙O上一点,弧CB=弧CE,连接AE并延长与DC的延长线交于点F.(1)求证:DC是⊙O的切线; (2)若⊙O的半径为3, sinD=,求线段AF的长 拓展,强化,为下面的复习做好准备
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
