沪科版数学八年级下册 18.1 勾股定理课件(共19张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 18.1 勾股定理课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 938.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-13 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
18.1 勾股定理
这个图案是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”.
这就是本届大会会徽的图案.
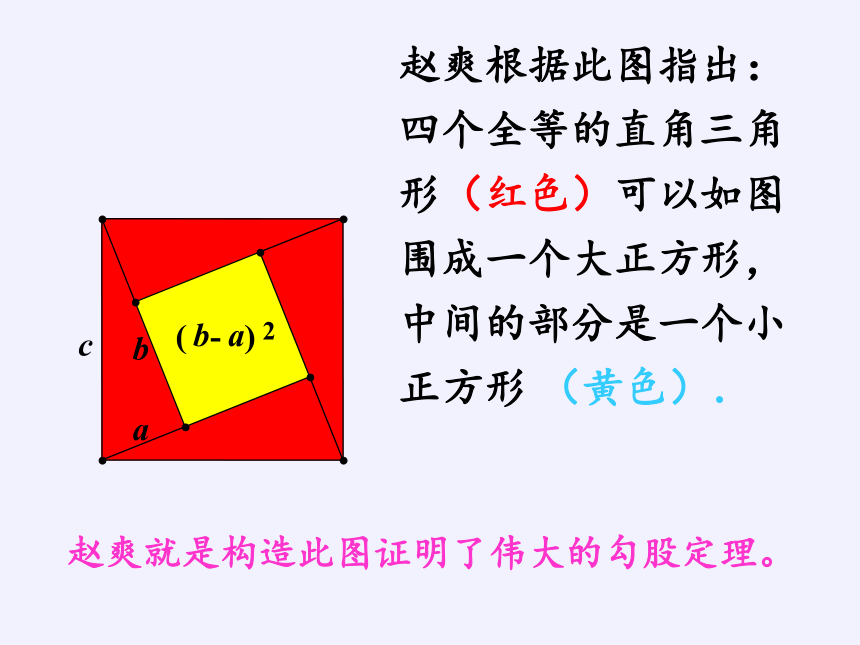
赵爽根据此图指出:四个全等的直角三角形(红色)可以如图围成一个大正方形,中间的部分是一个小正方形 (黄色).
赵爽就是构造此图证明了伟大的勾股定理。
c
b
a
(
b
-
a
)
2
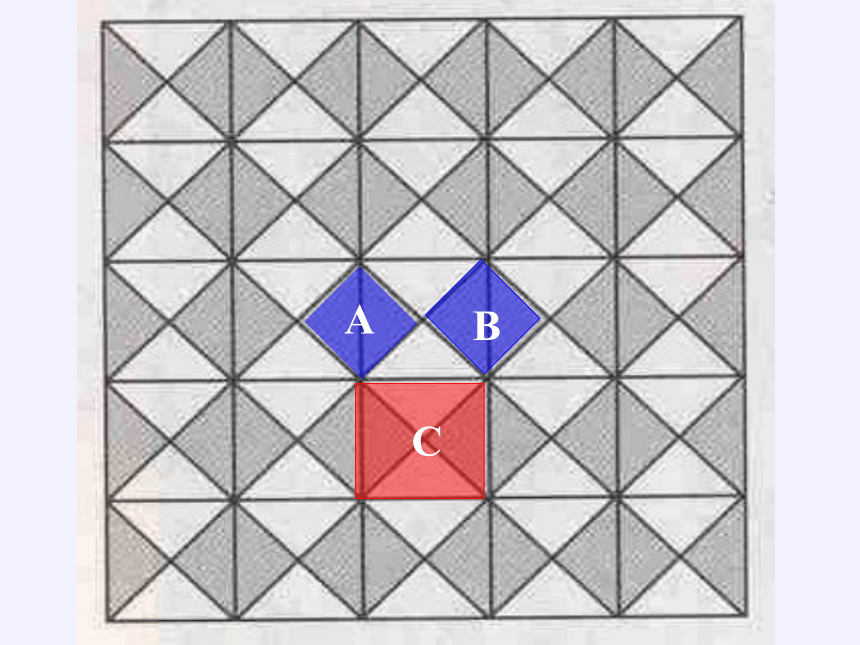
相传2500年前,古希腊著名的数学家毕达哥拉斯有一次在朋友家里做客时,发现朋友家用地砖铺成的地面中反映了直角三角形三边的某种数量关系.
我们也来观察右图中的地面,看看有什么发现?
情景问题
A
B
C
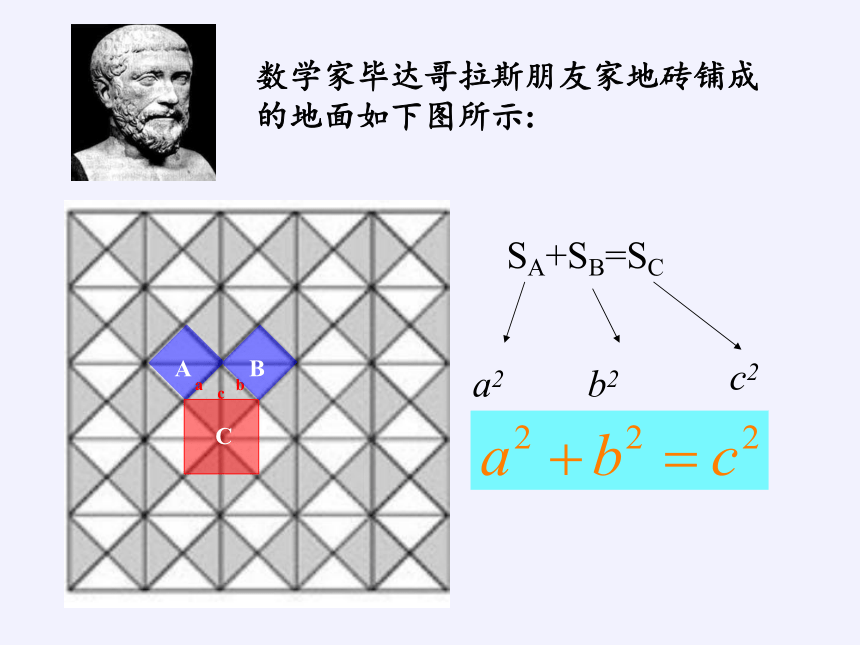
数学家毕达哥拉斯朋友家地砖铺成的地面如下图所示:
SA+SB=SC
a2
b2
c2
c
A
C
b
a
B
对于等腰直角三角形它的三边有这样的性质:
等腰直角三角形的三边有这样的性质,那么对于一般的直角三角形是否也有这样的性质呢?
归纳小结:
两直角边的平方和等于斜边的平方。
思考
A
B
C
图1
A
B
C
图2
观察右边两个图并填写下表:
A的面积 B的面积 C的面积
图1
图2
16
9
25
4
9
13
sA+sB=sC
a
b
c
探究
a
b
c
猜想:
直角三角形三边有怎样的的关系
命题:直角三角形两直角边的平方和等于斜边的平方
图1
图2
a
b
c
a
b
c
用赵爽弦图证明猜想
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲。正因为此,这个图案被选为2002年在北京召开的国际数学家大会的会徽。
c
b
a
①
②
③
④
⑤
赵爽弦图
大正方形的面积可表示为:
_______________________
大正方形的面积还可表示为:____
C2
化简后:a2+b2=c2
如图,在Rt△ ABC中,三边分别为a,b,c ∠ C=90°, 那么
a2+b2=c2
a
c
b
B
A
C
┏
直角三角形两直角边的平方和等于斜边的平方.
勾股定理:
勾股定理是人类最伟大的科学发现之一 .
文字语言:
符号语言:
小试牛刀
判断题
1、在△ABC中,a、b、c分别为三边,则a2+b2=c2
2、在Rt△ABC中,a、b、c分别为三边,则a2+b2=c2
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”。
我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
勾
股
弦
比一比看看谁算得快!
求下列直角三角形中未知边的长:
可用勾股定理建立方程.
方法小结:
x
4
5
x
12
5
x
练习
如图:一块长约40步、宽约30步的长方形草坪,被不自觉的学
生沿图中的虚线踏出了一条“捷径”,类似的现象也时有发生。
请问同学们:
(1)走“捷径”的原因是什么?为什么?
(2)“捷径”比正路(沿C→B→A)近_______步
应用性练习
30步
40步
A
B
C
例:如图,为得到池塘两岸A点和B点间的距离,
观测者在C点设桩,使△ABC为直角三角形,并测得
AC为100米,BC为80米.求A、B两点间的距离是多少?
A
B
C
解:在Rt △ABC中,∠B=90°
∴ AB2+BC2 =AC2
∴AB2 =AC2-BC2
=1002 - 802=602
∴AB=60
答:A、B两点间的距离是60米.
定理应用
本节课你学到了什么
1、勾股定理:直角三角形两直角边的平方和等于斜边的平方;
2、勾股定理的应用:已知直角三角形的任意两边求第三边。
3、体会数形结合的思想、特殊到一般的数学思想。
作业
1、必做题:课本P57页习题18.1第1、2、3题
2、课外探索:你还想知道“勾股定理”的其它证法吗?请上网查询,你一定有精彩的发现。若你再能写一点有关“勾股定理”的小文章,那就更漂亮了。
谢 谢
18.1 勾股定理
这个图案是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”.
这就是本届大会会徽的图案.
赵爽根据此图指出:四个全等的直角三角形(红色)可以如图围成一个大正方形,中间的部分是一个小正方形 (黄色).
赵爽就是构造此图证明了伟大的勾股定理。
c
b
a
(
b
-
a
)
2
相传2500年前,古希腊著名的数学家毕达哥拉斯有一次在朋友家里做客时,发现朋友家用地砖铺成的地面中反映了直角三角形三边的某种数量关系.
我们也来观察右图中的地面,看看有什么发现?
情景问题
A
B
C
数学家毕达哥拉斯朋友家地砖铺成的地面如下图所示:
SA+SB=SC
a2
b2
c2
c
A
C
b
a
B
对于等腰直角三角形它的三边有这样的性质:
等腰直角三角形的三边有这样的性质,那么对于一般的直角三角形是否也有这样的性质呢?
归纳小结:
两直角边的平方和等于斜边的平方。
思考
A
B
C
图1
A
B
C
图2
观察右边两个图并填写下表:
A的面积 B的面积 C的面积
图1
图2
16
9
25
4
9
13
sA+sB=sC
a
b
c
探究
a
b
c
猜想:
直角三角形三边有怎样的的关系
命题:直角三角形两直角边的平方和等于斜边的平方
图1
图2
a
b
c
a
b
c
用赵爽弦图证明猜想
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲。正因为此,这个图案被选为2002年在北京召开的国际数学家大会的会徽。
c
b
a
①
②
③
④
⑤
赵爽弦图
大正方形的面积可表示为:
_______________________
大正方形的面积还可表示为:____
C2
化简后:a2+b2=c2
如图,在Rt△ ABC中,三边分别为a,b,c ∠ C=90°, 那么
a2+b2=c2
a
c
b
B
A
C
┏
直角三角形两直角边的平方和等于斜边的平方.
勾股定理:
勾股定理是人类最伟大的科学发现之一 .
文字语言:
符号语言:
小试牛刀
判断题
1、在△ABC中,a、b、c分别为三边,则a2+b2=c2
2、在Rt△ABC中,a、b、c分别为三边,则a2+b2=c2
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”。
我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
勾
股
弦
比一比看看谁算得快!
求下列直角三角形中未知边的长:
可用勾股定理建立方程.
方法小结:
x
4
5
x
12
5
x
练习
如图:一块长约40步、宽约30步的长方形草坪,被不自觉的学
生沿图中的虚线踏出了一条“捷径”,类似的现象也时有发生。
请问同学们:
(1)走“捷径”的原因是什么?为什么?
(2)“捷径”比正路(沿C→B→A)近_______步
应用性练习
30步
40步
A
B
C
例:如图,为得到池塘两岸A点和B点间的距离,
观测者在C点设桩,使△ABC为直角三角形,并测得
AC为100米,BC为80米.求A、B两点间的距离是多少?
A
B
C
解:在Rt △ABC中,∠B=90°
∴ AB2+BC2 =AC2
∴AB2 =AC2-BC2
=1002 - 802=602
∴AB=60
答:A、B两点间的距离是60米.
定理应用
本节课你学到了什么
1、勾股定理:直角三角形两直角边的平方和等于斜边的平方;
2、勾股定理的应用:已知直角三角形的任意两边求第三边。
3、体会数形结合的思想、特殊到一般的数学思想。
作业
1、必做题:课本P57页习题18.1第1、2、3题
2、课外探索:你还想知道“勾股定理”的其它证法吗?请上网查询,你一定有精彩的发现。若你再能写一点有关“勾股定理”的小文章,那就更漂亮了。
谢 谢
