选择性必修三第二章气体、固体、液体:第3节 气体的等压变化和等容变化习题课(共16张ppt)
文档属性
| 名称 | 选择性必修三第二章气体、固体、液体:第3节 气体的等压变化和等容变化习题课(共16张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-06-13 14:55:30 | ||
图片预览






文档简介
(共16张PPT)
选择性必修三第二章 气体、固体、液体
第3节 气体的等压变化和等容变化习题课
复习:
1.气体等压变化的内容、公式、条件以及对应的图像是什么?
2.气体等容变化的内容、公式、条件以及对应的图像是什么?
(1)内容:一定质量的某种气体,在压强不变的情况下,其体积V与热力学温度T成正比。
(2)公式: (C为比例常数)或 。
(3)条件:气体质量一定,压强不变。
(1)内容:一定质量的某种气体,在体积不变的情况下,其压强P与热力学温度T成正比。
(2)公式: (C为比例常数)或 。
(3)条件:气体质量一定,体积不变。
3.理想气体状态方程是?
条件:一定质量的理想气体
一、气体的等压变化
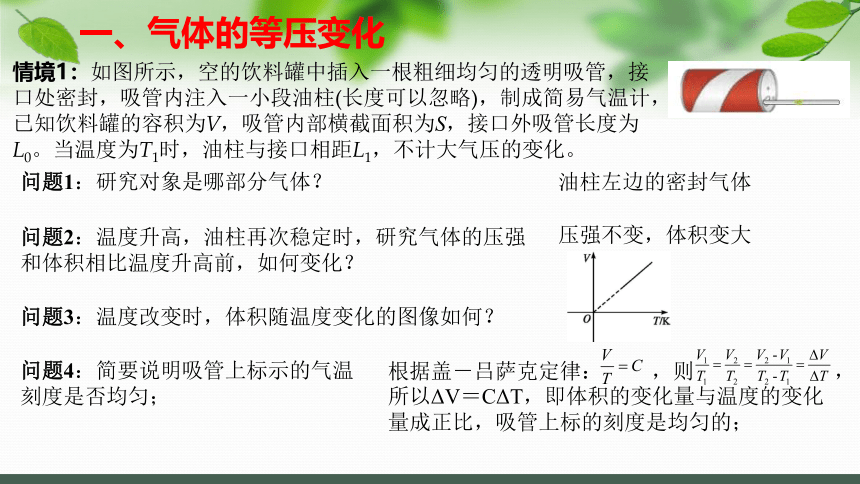
情境1:如图所示,空的饮料罐中插入一根粗细均匀的透明吸管,接口处密封,吸管内注入一小段油柱(长度可以忽略),制成简易气温计,已知饮料罐的容积为V,吸管内部横截面积为S,接口外吸管长度为L0。当温度为T1时,油柱与接口相距L1,不计大气压的变化。
问题1:研究对象是哪部分气体?
问题2:温度升高,油柱再次稳定时,研究气体的压强和体积相比温度升高前,如何变化?
问题3:温度改变时,体积随温度变化的图像如何?
油柱左边的密封气体
压强不变,体积变大
问题4:简要说明吸管上标示的气温刻度是否均匀;
根据盖-吕萨克定律: ,则 ,所以ΔV=CΔT,即体积的变化量与温度的变化量成正比,吸管上标的刻度是均匀的;
一、气体的等压变化
情境1:如图所示,空的饮料罐中插入一根粗细均匀的透明吸管,接口处密封,吸管内注入一小段油柱(长度可以忽略),制成简易气温计,已知饮料罐的容积为V,吸管内部横截面积为S,接口外吸管长度为L0。当温度为T1时,油柱与接口相距L1,不计大气压的变化。
问题6:求气温计能测量的最高温度Tm。
问题7:若已知罐的容积是360cm3,横截面积为0.2cm2,吸管有效长度为20cm,当温度为250C时,油柱离管口10cm。若给吸管上标刻温度值,试估算这个气温计的测量范围。
温度最低时:
温度最高时:
测温范围:
问题5:温度最低和最高时,吸管中的油柱在哪个位置?
温度最低:吸管最左端;
温度最高:吸管最右端。
一、气体的等压变化
一、气体的等压变化
情境变式1-1:温度计是生活、生产中常用的测温装置。右图为一个简单温度计,一根装有一小段有色水柱的细玻璃管穿过橡皮塞插入烧瓶内,封闭一定质量的气体。当外界温度发生变化时,水柱位置将上下变化。已知A、D间的测量范围为20℃~80℃,A、D间刻度均匀分布。由图可知,A、D及有色水柱下端所示的温度分别是 ( )
A.20℃、80℃、64℃ B.20℃、80℃、68℃
C.80℃、20℃、32℃ D.80℃、20℃、34℃
C
D
B
A
设D点下容器的体积为V, 一小格玻璃管的体积为V0。
C
解得
t=32℃
A处,气体体积最大,温度最高,为80℃;
D处,气体体积最小,温度最低,为20℃;
D刻度:V,T=(273+20)K
A刻度:V+15V0,T’=(273+80)K
D刻度:V,T=(273+20)K
油柱所在刻度:V+3V0,T’=(273+t)K
一、气体的等压变化
情境变式1-2:房间里气温升高3 ℃时,房间内的空气将有1%逸出到房间外,由此可计算出房间内原来的温度是( )
A.-7 ℃ B.7 ℃ C.17 ℃ D.27 ℃
解析:以升温前房间里的气体为研究对象,大气压强不变:
初状态:房间内的空气体积为V0,温度为T0;
末状态:空气体积为V0(1+1%),温度为T0+3;
由盖-吕萨克定律:
二、气体的等容变化
情境2:汽车行驶时轮胎的胎压太高容易造成爆胎事故,太低会造成耗油上升.已知某型号轮胎能在-40 ℃~90 ℃正常工作,为使轮胎在此温度范围内工作时的最高胎压不超过3.5 atm,最低胎压不低于1.6 atm。(设轮胎容积不变)
问题1:研究对象是哪部分气体?
胎内气体
问题2:胎内气体温度升高,稳定后,胎内气体的压强和体积与升温前相比,如何变化?
体积不变,压强变大。
问题3:胎内气体温度改变时,压强随温度变化的图像如何?
问题4:轮胎能在-40 ℃~90 ℃正常工作时,哪个温度胎压最低?哪个温度胎压最高?
压强与绝对温度T成正比。故-40 ℃时,胎压最低;90 ℃时,胎压最高。
二、气体的等容变化
情境2:汽车行驶时轮胎的胎压太高容易造成爆胎事故,太低会造成耗油上升.已知某型号轮胎能在-40 ℃~90 ℃正常工作,为使轮胎在此温度范围内工作时的最高胎压不超过3.5 atm,最低胎压不低于1.6 atm。(设轮胎容积不变)
设在t=20 ℃时,即T0=293K时,充气后胎压为Pmin,t=-40 ℃,即T1=233K时,压强为P1=1.6 atm.
问题5:为保证最低胎压不低于1.6 atm,那么t=20 ℃时给该轮胎充气,充气后的胎压应满足什么条件?
问题6:为保证最高胎压不超过3.5 atm,那么t=20 ℃时给该轮胎充气,充气后的胎压应满足什么条件?
设在t=20 ℃时,即T0=293K时,充气后胎压为Pmax,t=90 ℃,即T2=363K时,压强为P2=3.5 atm.
即,t=20 ℃时给该轮胎充气,充气后的胎压范围为
二、气体的等容变化
二、气体的等容变化
情境变式2-1:灯泡内充有氮氩混合气体,如果要使灯泡内的混合气体在500℃时的压强不超过1atm,在20℃下充气,灯泡内气体的压强至多能充到多少?
解析:以灯泡内气体为研究对象,温度升高时体积不变。
初状态:温度为t1=20℃,故T1=(273+20) K,压强为p1;
末状态:温度为t2=500℃,故T2=(273+500) K,压强为p2=1atm.
应用查理定律即可求出初状态的压强.
二、气体的等容变化
情境变式2-2:某登山运动员在一次攀登珠穆朗玛峰的过程中,在接近山顶时他裸露在手腕上的防水手表的表盘玻璃突然爆裂了,而手表没有受到任何撞击。该手表出厂时给出的参数为:27 ℃时表内气体压强为1.0×105 Pa(常温下的大气压强值),当内外压强差超过6.0×104 Pa时表盘玻璃将爆裂。当时登山运动员携带的温度计的读数是-21 ℃,表内气体体积的变化可忽略不计。
(1)通过计算判断手表的表盘玻璃是向外爆裂还是向内爆裂?
(2)当时外界的大气压强为多少?
解析:(1)以表内气体为研究对象,则
初状态:p1=1.0×105 Pa,T1=300 K,
末状态:压强为p2,温度为T2=252 K
如果是向内爆裂,则外界大气压强为p0=8.4×104 Pa+6×104 Pa=1.44×105 Pa,大于山脚下大气压(即常温大气压),这是不可能的,所以表盘玻璃是向外爆裂的
解析:(2)当时外界大气压强为p0=p2-6×104 Pa=8.4×104 Pa-6×104 Pa=2.4×104 Pa
二、气体的等容变化
情境变式2-3:1697年法国物理学家帕平发明了高压锅,高压锅与普通铝锅不同,锅盖通过几个牙齿似的锅齿与锅体镶嵌旋紧,加上锅盖与锅体之间有橡皮制的密封圈,所以锅盖与锅体之间不会漏气,在锅盖中间有一排气孔,上面再套上类似砝码的限压阀,将排气孔堵住.当加热高压锅,锅内气体压强增加到一定程度时,气体就把限压阀顶起来,这时蒸气就从排气孔向外排出.由于高压锅内的压强大,温度高,食物容易煮烂.若已知排气孔的直径为0.3cm,外界大气压为1.0×105Pa,温度为20℃,要使高压锅内的温度达到120℃,则限压阀的质量应为多少?
解析:选锅内气体为研究对象,则
初状态:T1=293 K,p1=1.0×105 Pa,
末状态:T2=393 K.
由查理定律得
对限压阀受力分析,得
所以限压阀质量应为 m=0.024kg
三、理想气体状态方程
情境变式2-4:某人用打气筒给闲置很久的电动自行车打气,电动自行车内胎的容积为V=1.8L,胎内原来空气压强等于标准大气压强 ,温度为室温27℃,设每打一次可打入压强为一个标准大气压的空气120cm3。打气过程中由于压缩气体做功和摩擦生热,打了30次后胎内温度升高到33℃。假设车胎因膨胀而增大的体积可以忽略不计,则此时车胎内空气压强为多少;
解析:为保证气体质量不变,研究对象为胎内气体与30次打气筒内气体的总和
初状态:T1=300 K,p1=1.0×105 Pa,V1=1.8L+30*0.12L=5.4L
末状态:T2=306 K,p2, V2=1.8L
研究气体的温度、体积和压强都发生了改变,不再适用盖-吕萨克定律和查理定律
可由理想气体状态方程可得
一、气体的等压变化
1.条件:气体质量一定,压强不变。
2.公式: (C为比例常数)或
二、气体的等容变化
1.条件:气体质量一定,体积不变。
2.公式: (C为比例常数)或
三、理想气体状态方程
1.条件:一定质量的理想气体。
2.公式: (C为比例常数)或
应用气体状态方程解题的一般步骤
(1)确定研究对象,即被封闭的气体.
(2)分析被研究气体在状态变化时是否符合定律的适用条件:
质量一定,压强不变,适用盖吕萨克定律;
质量一定,体积不变,适用查理定律;
质量一定,压强、体积和温度都改变,适用理想气体状态方程;
(3)确定初、末两个状态的热力学温度、压强和体积.
(4)根据列式求解,并对结果分析、检验.
谢谢
选择性必修三第二章 气体、固体、液体
第3节 气体的等压变化和等容变化习题课
复习:
1.气体等压变化的内容、公式、条件以及对应的图像是什么?
2.气体等容变化的内容、公式、条件以及对应的图像是什么?
(1)内容:一定质量的某种气体,在压强不变的情况下,其体积V与热力学温度T成正比。
(2)公式: (C为比例常数)或 。
(3)条件:气体质量一定,压强不变。
(1)内容:一定质量的某种气体,在体积不变的情况下,其压强P与热力学温度T成正比。
(2)公式: (C为比例常数)或 。
(3)条件:气体质量一定,体积不变。
3.理想气体状态方程是?
条件:一定质量的理想气体
一、气体的等压变化
情境1:如图所示,空的饮料罐中插入一根粗细均匀的透明吸管,接口处密封,吸管内注入一小段油柱(长度可以忽略),制成简易气温计,已知饮料罐的容积为V,吸管内部横截面积为S,接口外吸管长度为L0。当温度为T1时,油柱与接口相距L1,不计大气压的变化。
问题1:研究对象是哪部分气体?
问题2:温度升高,油柱再次稳定时,研究气体的压强和体积相比温度升高前,如何变化?
问题3:温度改变时,体积随温度变化的图像如何?
油柱左边的密封气体
压强不变,体积变大
问题4:简要说明吸管上标示的气温刻度是否均匀;
根据盖-吕萨克定律: ,则 ,所以ΔV=CΔT,即体积的变化量与温度的变化量成正比,吸管上标的刻度是均匀的;
一、气体的等压变化
情境1:如图所示,空的饮料罐中插入一根粗细均匀的透明吸管,接口处密封,吸管内注入一小段油柱(长度可以忽略),制成简易气温计,已知饮料罐的容积为V,吸管内部横截面积为S,接口外吸管长度为L0。当温度为T1时,油柱与接口相距L1,不计大气压的变化。
问题6:求气温计能测量的最高温度Tm。
问题7:若已知罐的容积是360cm3,横截面积为0.2cm2,吸管有效长度为20cm,当温度为250C时,油柱离管口10cm。若给吸管上标刻温度值,试估算这个气温计的测量范围。
温度最低时:
温度最高时:
测温范围:
问题5:温度最低和最高时,吸管中的油柱在哪个位置?
温度最低:吸管最左端;
温度最高:吸管最右端。
一、气体的等压变化
一、气体的等压变化
情境变式1-1:温度计是生活、生产中常用的测温装置。右图为一个简单温度计,一根装有一小段有色水柱的细玻璃管穿过橡皮塞插入烧瓶内,封闭一定质量的气体。当外界温度发生变化时,水柱位置将上下变化。已知A、D间的测量范围为20℃~80℃,A、D间刻度均匀分布。由图可知,A、D及有色水柱下端所示的温度分别是 ( )
A.20℃、80℃、64℃ B.20℃、80℃、68℃
C.80℃、20℃、32℃ D.80℃、20℃、34℃
C
D
B
A
设D点下容器的体积为V, 一小格玻璃管的体积为V0。
C
解得
t=32℃
A处,气体体积最大,温度最高,为80℃;
D处,气体体积最小,温度最低,为20℃;
D刻度:V,T=(273+20)K
A刻度:V+15V0,T’=(273+80)K
D刻度:V,T=(273+20)K
油柱所在刻度:V+3V0,T’=(273+t)K
一、气体的等压变化
情境变式1-2:房间里气温升高3 ℃时,房间内的空气将有1%逸出到房间外,由此可计算出房间内原来的温度是( )
A.-7 ℃ B.7 ℃ C.17 ℃ D.27 ℃
解析:以升温前房间里的气体为研究对象,大气压强不变:
初状态:房间内的空气体积为V0,温度为T0;
末状态:空气体积为V0(1+1%),温度为T0+3;
由盖-吕萨克定律:
二、气体的等容变化
情境2:汽车行驶时轮胎的胎压太高容易造成爆胎事故,太低会造成耗油上升.已知某型号轮胎能在-40 ℃~90 ℃正常工作,为使轮胎在此温度范围内工作时的最高胎压不超过3.5 atm,最低胎压不低于1.6 atm。(设轮胎容积不变)
问题1:研究对象是哪部分气体?
胎内气体
问题2:胎内气体温度升高,稳定后,胎内气体的压强和体积与升温前相比,如何变化?
体积不变,压强变大。
问题3:胎内气体温度改变时,压强随温度变化的图像如何?
问题4:轮胎能在-40 ℃~90 ℃正常工作时,哪个温度胎压最低?哪个温度胎压最高?
压强与绝对温度T成正比。故-40 ℃时,胎压最低;90 ℃时,胎压最高。
二、气体的等容变化
情境2:汽车行驶时轮胎的胎压太高容易造成爆胎事故,太低会造成耗油上升.已知某型号轮胎能在-40 ℃~90 ℃正常工作,为使轮胎在此温度范围内工作时的最高胎压不超过3.5 atm,最低胎压不低于1.6 atm。(设轮胎容积不变)
设在t=20 ℃时,即T0=293K时,充气后胎压为Pmin,t=-40 ℃,即T1=233K时,压强为P1=1.6 atm.
问题5:为保证最低胎压不低于1.6 atm,那么t=20 ℃时给该轮胎充气,充气后的胎压应满足什么条件?
问题6:为保证最高胎压不超过3.5 atm,那么t=20 ℃时给该轮胎充气,充气后的胎压应满足什么条件?
设在t=20 ℃时,即T0=293K时,充气后胎压为Pmax,t=90 ℃,即T2=363K时,压强为P2=3.5 atm.
即,t=20 ℃时给该轮胎充气,充气后的胎压范围为
二、气体的等容变化
二、气体的等容变化
情境变式2-1:灯泡内充有氮氩混合气体,如果要使灯泡内的混合气体在500℃时的压强不超过1atm,在20℃下充气,灯泡内气体的压强至多能充到多少?
解析:以灯泡内气体为研究对象,温度升高时体积不变。
初状态:温度为t1=20℃,故T1=(273+20) K,压强为p1;
末状态:温度为t2=500℃,故T2=(273+500) K,压强为p2=1atm.
应用查理定律即可求出初状态的压强.
二、气体的等容变化
情境变式2-2:某登山运动员在一次攀登珠穆朗玛峰的过程中,在接近山顶时他裸露在手腕上的防水手表的表盘玻璃突然爆裂了,而手表没有受到任何撞击。该手表出厂时给出的参数为:27 ℃时表内气体压强为1.0×105 Pa(常温下的大气压强值),当内外压强差超过6.0×104 Pa时表盘玻璃将爆裂。当时登山运动员携带的温度计的读数是-21 ℃,表内气体体积的变化可忽略不计。
(1)通过计算判断手表的表盘玻璃是向外爆裂还是向内爆裂?
(2)当时外界的大气压强为多少?
解析:(1)以表内气体为研究对象,则
初状态:p1=1.0×105 Pa,T1=300 K,
末状态:压强为p2,温度为T2=252 K
如果是向内爆裂,则外界大气压强为p0=8.4×104 Pa+6×104 Pa=1.44×105 Pa,大于山脚下大气压(即常温大气压),这是不可能的,所以表盘玻璃是向外爆裂的
解析:(2)当时外界大气压强为p0=p2-6×104 Pa=8.4×104 Pa-6×104 Pa=2.4×104 Pa
二、气体的等容变化
情境变式2-3:1697年法国物理学家帕平发明了高压锅,高压锅与普通铝锅不同,锅盖通过几个牙齿似的锅齿与锅体镶嵌旋紧,加上锅盖与锅体之间有橡皮制的密封圈,所以锅盖与锅体之间不会漏气,在锅盖中间有一排气孔,上面再套上类似砝码的限压阀,将排气孔堵住.当加热高压锅,锅内气体压强增加到一定程度时,气体就把限压阀顶起来,这时蒸气就从排气孔向外排出.由于高压锅内的压强大,温度高,食物容易煮烂.若已知排气孔的直径为0.3cm,外界大气压为1.0×105Pa,温度为20℃,要使高压锅内的温度达到120℃,则限压阀的质量应为多少?
解析:选锅内气体为研究对象,则
初状态:T1=293 K,p1=1.0×105 Pa,
末状态:T2=393 K.
由查理定律得
对限压阀受力分析,得
所以限压阀质量应为 m=0.024kg
三、理想气体状态方程
情境变式2-4:某人用打气筒给闲置很久的电动自行车打气,电动自行车内胎的容积为V=1.8L,胎内原来空气压强等于标准大气压强 ,温度为室温27℃,设每打一次可打入压强为一个标准大气压的空气120cm3。打气过程中由于压缩气体做功和摩擦生热,打了30次后胎内温度升高到33℃。假设车胎因膨胀而增大的体积可以忽略不计,则此时车胎内空气压强为多少;
解析:为保证气体质量不变,研究对象为胎内气体与30次打气筒内气体的总和
初状态:T1=300 K,p1=1.0×105 Pa,V1=1.8L+30*0.12L=5.4L
末状态:T2=306 K,p2, V2=1.8L
研究气体的温度、体积和压强都发生了改变,不再适用盖-吕萨克定律和查理定律
可由理想气体状态方程可得
一、气体的等压变化
1.条件:气体质量一定,压强不变。
2.公式: (C为比例常数)或
二、气体的等容变化
1.条件:气体质量一定,体积不变。
2.公式: (C为比例常数)或
三、理想气体状态方程
1.条件:一定质量的理想气体。
2.公式: (C为比例常数)或
应用气体状态方程解题的一般步骤
(1)确定研究对象,即被封闭的气体.
(2)分析被研究气体在状态变化时是否符合定律的适用条件:
质量一定,压强不变,适用盖吕萨克定律;
质量一定,体积不变,适用查理定律;
质量一定,压强、体积和温度都改变,适用理想气体状态方程;
(3)确定初、末两个状态的热力学温度、压强和体积.
(4)根据列式求解,并对结果分析、检验.
谢谢
同课章节目录
- 第一章 分子动理论
- 1 分子动理论的基本内容
- 2 实验:用油膜法估测油酸分子的大小
- 3 分子运动速率分布规律
- 4 分子动能和分子势能
- 第二章 气体、固体和液体
- 1 温度和温标
- 2 气体的等温变化
- 3 气体的等压变化和等容变化
- 4 固体
- 5 液体
- 第三章 热力学定律
- 1 功、热和内能的改变
- 2 热力学第一定律
- 3 能量守恒定律
- 4 热力学第二定律
- 第四章 原子结构和波粒二象性
- 1 普朗克黑体辐射理论
- 2 光电效应
- 3 原子的核式结构模型
- 4 氢原子光谱和玻尔的原子模型
- 5 粒子的波动性和量子力学的建立
- 第五章 原子核
- 1 原子核的组成
- 2 放射性元素的衰变
- 3 核力与结合能
- 4 核裂变与核聚变
- 5 “基本”粒子
