第十八章 平行四边形 章末复习课件(共31张PPT)
文档属性
| 名称 | 第十八章 平行四边形 章末复习课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-24 11:39:50 | ||
图片预览









文档简介
(共31张PPT)
第十八章 平行四边形
章末复习
人教版 八年级下册
教学目标
学习目标:
1.回顾平行四边形特殊四边形的性质与判定,三角形的中位线及其性质,直角三角形斜边上的中线的性质.
2.总结本章的重要思想方法.
重点:
平行四边形的性质和判定,特殊四边形的性质和判定.
难点:
几种特殊平行四边形之间的联系和区别.
归纳总结
平行四边形的性质及判定
1.定义:两组对边分别平行的四边形叫做平行四边形.
平行四边形用“□”表示,如图,平行四边形ABCD记作“□ABCD ”.
平行四边形的对边相等.
平行四边形的对角相等.
2.平行四边形的性质除了对边互相平行以外,还有:
平行四边形的对角线互相平分.
归纳总结
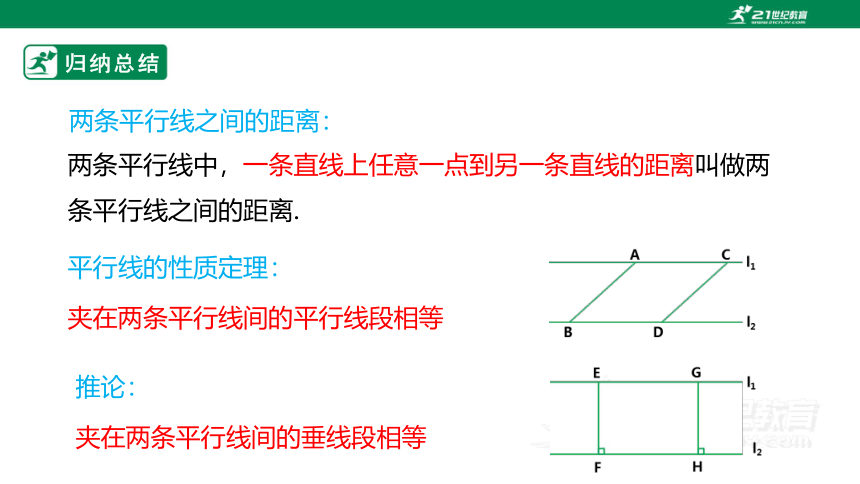
两条平行线之间的距离:
两条平行线中,一条直线上任意一点到另一条直线的距离叫做两条平行线之间的距离.
平行线的性质定理:
夹在两条平行线间的平行线段相等
推论:
夹在两条平行线间的垂线段相等
归纳总结
3.平行四边形的判定:
两组对边分别相等的四边形是平行四边形.
判定定理1
两组对角分别相等的四边形是平行四边形.
判定定理2
对角线互相平分的四边形是平行四边形.
判定定理3
判定定理4
一组对边平行且相等的四边形是平行四边形.
判定定理5
两组对边分别平行的四边形叫做平行四边形.
归纳总结
三角形的中位线定理:
三角形的中位线平行于第三边,并且等于第三边的一半.
几何语言:
∵DE是△ABC的中位线(或 AD=BD,AE=CE),
∴DE= BC, DE//BC.
D
E
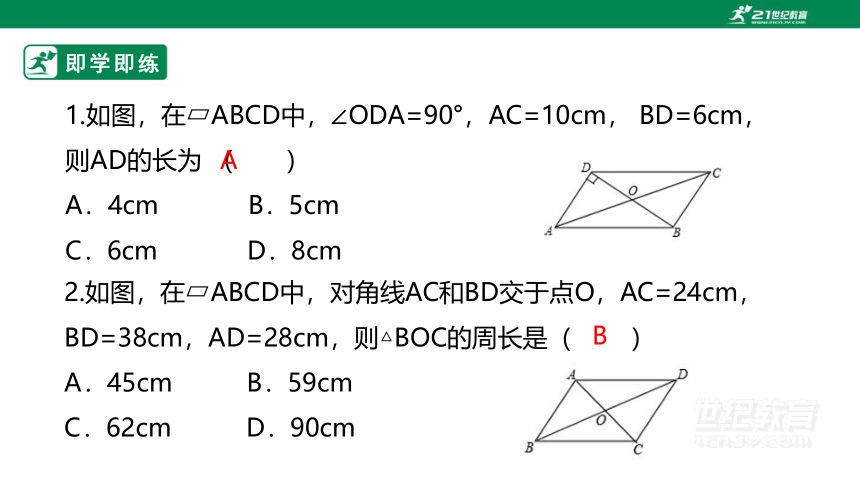
2.如图,在 ABCD中,对角线AC和BD交于点O,AC=24cm,BD=38cm,AD=28cm,则△BOC的周长是( )
A.45cm B.59cm
C.62cm D.90cm
即学即练
B
1.如图,在 ABCD中,∠ODA=90°,AC=10cm, BD=6cm,则AD的长为 ( )
A.4cm B.5cm
C.6cm D.8cm
A
即学即练
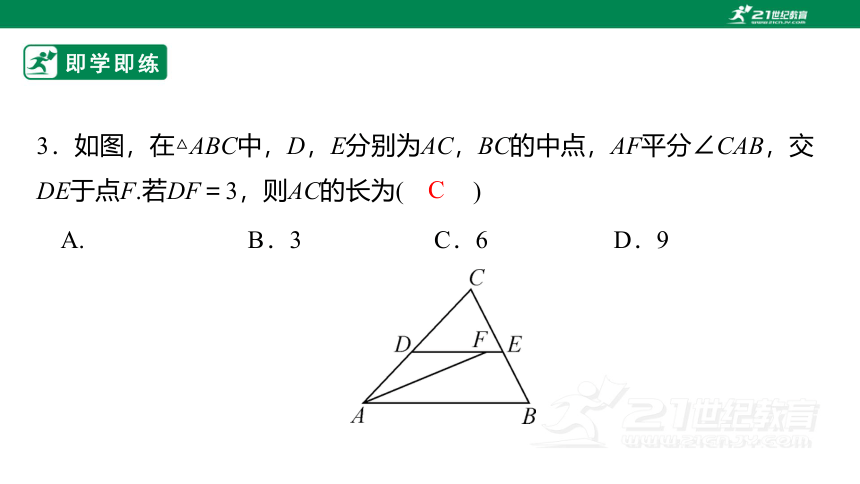
A. B.3 C.6 D.9
3.如图,在△ABC中,D,E分别为AC,BC的中点,AF平分∠CAB,交DE于点F.若DF=3,则AC的长为( )
C
证明:∵四边形ABCD是平行四边形,
∴∠B=∠D,AD=BC,AB=CD,∠BAD=∠BCD,
∵AE平分∠BAD,CF平分∠BCD,
∴∠EAB= ∠BAD,∠FCD= ∠BCD,∴∠EAB= ∠FCD,
在△ABE和△CDF中
∠B=∠D,
AB=CD , ∴△ABE≌△CDF,∴BE=DF.
∠EAB=∠FCD, ∵AD=BC , ∴AF=EC.
即学即练
4.如图,已知 ABCD中,AE平分∠BAD,CF平分∠BCD,分别交BC、AD于E、F.求证:AF=EC.
即学即练
5.如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:
AP=_____; DP=________;
BQ=________ ; CQ=________;
tcm
(12-t)cm
(15-2t)cm
2tcm
即学即练
(2)当t为何值时,四边形APQB是平行四边形?
解:根据题意有AP=tcm,CQ=2tcm,
PD=(12-t)cm,BQ=(15-2t)cm.
∵AD∥BC,
∴当AP=BQ时,四边形APQB是平行四边形.
∴t=15-2t,
解得t=5.
∴t=5s时四边形APQB是平行四边形.
即学即练
解:∵AP=tcm,CQ=2tcm,AD=12cm,
∴PD=AD-AP=(12-t)cm,
∵AD∥BC,
∴当PD=QC时,四边形PDCQ是平行四边形.
即12-t=2t,
解得t=4,
∴当t=4s时,四边形PDCQ是平行四边形.
(3)当t为何值时,四边形PDCQ是平行四边形?
归纳总结
矩形的性质及判定
1.定义:有一个角是直角的平行四边形叫做矩形.也叫做长方形.
矩形是特殊的平行四边形.
矩形除了具有平行四边形所有性质,还具有的性质有:
矩形的对角线相等
2.矩形的性质:
矩形的四个角都是直角
归纳总结
4.直角三角形的性质:
直角三角形斜边上的中线等于斜边的一半.
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形 .
(对角线相等且互相平分的四边形是矩形.)
有三个角是直角的四边形是矩形 .
方法1:
方法2:
方法3:
3.矩形的判定:
即学即练
1.如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则EF=______cm.
2.5
2.四边形ABCD的对角线AC,BD相交于点O,已知下列6个条件:①AB∥DC;②AB=DC;③AC=BD;④∠ABC=90°;⑤OA=OC;⑥OB=OD.能判定四边形ABCD是矩形的有_____________________________________.(填序号)
①②③(或①②④或③⑤⑥或④⑤⑥)
即学即练
3.如图,矩形ABCD的对角线相交于点O,E,F,G,H分别是OA,OB,OC,OD上的点,且AE=BF=CG=DH.
求证:四边形EFGH是矩形.
证明:∵四边形ABCD是矩形,
∴OA=OB=OC=OD.
∵AE=BF=CG=DH,
∴AO-AE=OB-BF=CO-CG=DO-DH,
即OE=OF=OG=OH,
∴四边形EFGH是矩形.
归纳总结
菱形的性质及判定
1.定义:有一组邻边相等的平行四边形叫做菱形.
菱形是特殊的平行四边形.
菱形除了具有平行四边形所有性质,还具有的性质有:
2.菱形的性质:
菱形的四条边都相等
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
归纳总结
3.菱形的判定:
有一组邻边相等的平行四边形叫做菱形
四条边都相等的四边形是菱形
对角线互相垂直的平行四边形是菱形.
方法1:
方法2:
方法3:
4.菱形是轴对称图形,它的两条对角线所在的直线都是它的对称轴,每条对角线平分一组对角.
即学即练
2.如图,在菱形ABCD中,对角线AC=10,BD=6,则菱形ABCD的面积为______.
30
A
B
C
O
D
1.如图,已知菱形的两条对角线长分别为6cm和8cm,则这个菱形的高DE为( )
A.2.4cm B.4.8cm C.5cm D.9.6cm
B
即学即练
3.如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE∥BD,过点D作ED∥AC,两线相交于点E.
求证:四边形AODE是菱形;
证明:∵AE∥BD,ED∥AC,
∴四边形AODE是平行四边形.
∵四边形ABCD是矩形,
∴AC=BD,OA=OC= AC,OB=OD= BD,
∴OA=OC=OD,
∴四边形AODE是菱形;
即学即练
解:(1)证明:由尺规作∠BAF的平分线的过程可得AB=AF,∠BAE=∠FAE,
∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠FAE=∠AEB,
∴∠BAE=∠AEB,∴AB=BE,
∴BE=FA,∴四边形ABEF为平行四边形,
∵AB=AF,∴四边形ABEF为菱形.
4.如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E,连接EF.
(1)求证:四边形ABEF为菱形;
即学即练
解:∵四边形ABEF为菱形,
∴AE⊥BF,BO= FB=3,AE=2AO,
在Rt△AOB中,由勾股定理得AO =4,
∴AE=2AO=8.
4.如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E,连接EF.
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.
归纳总结
正方形的性质及判定
1.定义:有一组邻边相等并且有一个角是直角的平行四边形叫正方形.
2.正方形的性质
正方形的四个角都是直角;
正方形的四条边都相等;
正方形的对角线相等,并且互相垂直平分;
正方形是轴对称图形,它有四条对称轴.
归纳总结
正方形
矩形
有一组邻边相等
菱形
有一个角是直角
有一组邻边相等
且有一个角是直角
3.正方形常见的判定方法
先证是矩形再证是菱形或先证是菱形再证是矩形
平行四边形
即学即练
2.如图,在正方形ABCD中,点E,H,F,G分别在边AB,BC,CD,DA上,EF,GH交于点O,∠FOH=90°, EF=4.则GH的长为 .
4
M
N
1.在正方形ABCD中,E是对角线AC上一点,且AE=AB,则∠EBC的度数是 .
A
D
B
C
O
E
22.5°
即学即练
3.如图,在四边形ABCD中, AB=BC ,对角线BD平分 ABC , P是BD上一点,过点P作PM AD , PN CD ,垂足分别为M、N.
(1) 求证: ADB= CDB;
C
A
B
D
P
M
N
证明:(1)∵BD平分∠ABC.
∴∠1=∠2.
又∵AB = BC,
∴△ABD≌△CBD (SAS).
∴∠ADB=∠CDB.
1
2
C
A
B
D
P
M
N
(2)∵PM⊥AD,PN⊥CD,∴∠PMD=∠PND=90°.
又∵∠ADC=90°,∴四边形NPMD是矩形.
∵∠ADB=∠CDB,
∴∠ADB=∠CDB=45°.
∴∠MPD=∠NPD=45°.
∴DM=PM,DN=PN.
∴四边形NPMD是正方形.
3.如图,在四边形ABCD中, AB=BC ,对角线BD平分 ABC , P是BD上一点,过点P作PM AD , PN CD ,垂足分别为M、N.
(2) 若 ADC=90 ,求证:四边形MPND是正方形.
即学即练
归纳总结
几种特殊四边形的性质汇总
项目 四边形 边 角 对角线 对称性
对边平行且相等
对边平行且相等
对边平行
且四边相等
对边平行
且四边相等
对角相等
四个角
都是直角
对角相等
四个角
都是直角
互相平分
互相平分且相等
互相垂直平分且相等,每一条对角线平分一组对角
轴对称图形
轴对称图形
轴对称图形
互相垂直且平分,每一条对角线平分一组对角
归纳总结
四边形 条件
几种特殊四边形的常用判定方法汇总:
1.定义:两组对边分别平行 2.两组对边分别相等
3.两组对角分别相等 4.对角线互相平分
5.一组对边平行且相等
1.定义:有一个角是直角的平行四边形
2.对角线相等的平行四边形
3.有三个角是直角的四边形
1.定义:一组邻边相等的平行四边形 ;2.对角线互相垂直的平行四边形,3.四条边都相等的四边形
1.定义:一组邻边相等且有一个角是直角的平行四边形
2.有一组邻边相等的矩形 3.有一个角是直角的菱形
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第十八章 平行四边形
章末复习
人教版 八年级下册
教学目标
学习目标:
1.回顾平行四边形特殊四边形的性质与判定,三角形的中位线及其性质,直角三角形斜边上的中线的性质.
2.总结本章的重要思想方法.
重点:
平行四边形的性质和判定,特殊四边形的性质和判定.
难点:
几种特殊平行四边形之间的联系和区别.
归纳总结
平行四边形的性质及判定
1.定义:两组对边分别平行的四边形叫做平行四边形.
平行四边形用“□”表示,如图,平行四边形ABCD记作“□ABCD ”.
平行四边形的对边相等.
平行四边形的对角相等.
2.平行四边形的性质除了对边互相平行以外,还有:
平行四边形的对角线互相平分.
归纳总结
两条平行线之间的距离:
两条平行线中,一条直线上任意一点到另一条直线的距离叫做两条平行线之间的距离.
平行线的性质定理:
夹在两条平行线间的平行线段相等
推论:
夹在两条平行线间的垂线段相等
归纳总结
3.平行四边形的判定:
两组对边分别相等的四边形是平行四边形.
判定定理1
两组对角分别相等的四边形是平行四边形.
判定定理2
对角线互相平分的四边形是平行四边形.
判定定理3
判定定理4
一组对边平行且相等的四边形是平行四边形.
判定定理5
两组对边分别平行的四边形叫做平行四边形.
归纳总结
三角形的中位线定理:
三角形的中位线平行于第三边,并且等于第三边的一半.
几何语言:
∵DE是△ABC的中位线(或 AD=BD,AE=CE),
∴DE= BC, DE//BC.
D
E
2.如图,在 ABCD中,对角线AC和BD交于点O,AC=24cm,BD=38cm,AD=28cm,则△BOC的周长是( )
A.45cm B.59cm
C.62cm D.90cm
即学即练
B
1.如图,在 ABCD中,∠ODA=90°,AC=10cm, BD=6cm,则AD的长为 ( )
A.4cm B.5cm
C.6cm D.8cm
A
即学即练
A. B.3 C.6 D.9
3.如图,在△ABC中,D,E分别为AC,BC的中点,AF平分∠CAB,交DE于点F.若DF=3,则AC的长为( )
C
证明:∵四边形ABCD是平行四边形,
∴∠B=∠D,AD=BC,AB=CD,∠BAD=∠BCD,
∵AE平分∠BAD,CF平分∠BCD,
∴∠EAB= ∠BAD,∠FCD= ∠BCD,∴∠EAB= ∠FCD,
在△ABE和△CDF中
∠B=∠D,
AB=CD , ∴△ABE≌△CDF,∴BE=DF.
∠EAB=∠FCD, ∵AD=BC , ∴AF=EC.
即学即练
4.如图,已知 ABCD中,AE平分∠BAD,CF平分∠BCD,分别交BC、AD于E、F.求证:AF=EC.
即学即练
5.如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:
AP=_____; DP=________;
BQ=________ ; CQ=________;
tcm
(12-t)cm
(15-2t)cm
2tcm
即学即练
(2)当t为何值时,四边形APQB是平行四边形?
解:根据题意有AP=tcm,CQ=2tcm,
PD=(12-t)cm,BQ=(15-2t)cm.
∵AD∥BC,
∴当AP=BQ时,四边形APQB是平行四边形.
∴t=15-2t,
解得t=5.
∴t=5s时四边形APQB是平行四边形.
即学即练
解:∵AP=tcm,CQ=2tcm,AD=12cm,
∴PD=AD-AP=(12-t)cm,
∵AD∥BC,
∴当PD=QC时,四边形PDCQ是平行四边形.
即12-t=2t,
解得t=4,
∴当t=4s时,四边形PDCQ是平行四边形.
(3)当t为何值时,四边形PDCQ是平行四边形?
归纳总结
矩形的性质及判定
1.定义:有一个角是直角的平行四边形叫做矩形.也叫做长方形.
矩形是特殊的平行四边形.
矩形除了具有平行四边形所有性质,还具有的性质有:
矩形的对角线相等
2.矩形的性质:
矩形的四个角都是直角
归纳总结
4.直角三角形的性质:
直角三角形斜边上的中线等于斜边的一半.
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形 .
(对角线相等且互相平分的四边形是矩形.)
有三个角是直角的四边形是矩形 .
方法1:
方法2:
方法3:
3.矩形的判定:
即学即练
1.如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则EF=______cm.
2.5
2.四边形ABCD的对角线AC,BD相交于点O,已知下列6个条件:①AB∥DC;②AB=DC;③AC=BD;④∠ABC=90°;⑤OA=OC;⑥OB=OD.能判定四边形ABCD是矩形的有_____________________________________.(填序号)
①②③(或①②④或③⑤⑥或④⑤⑥)
即学即练
3.如图,矩形ABCD的对角线相交于点O,E,F,G,H分别是OA,OB,OC,OD上的点,且AE=BF=CG=DH.
求证:四边形EFGH是矩形.
证明:∵四边形ABCD是矩形,
∴OA=OB=OC=OD.
∵AE=BF=CG=DH,
∴AO-AE=OB-BF=CO-CG=DO-DH,
即OE=OF=OG=OH,
∴四边形EFGH是矩形.
归纳总结
菱形的性质及判定
1.定义:有一组邻边相等的平行四边形叫做菱形.
菱形是特殊的平行四边形.
菱形除了具有平行四边形所有性质,还具有的性质有:
2.菱形的性质:
菱形的四条边都相等
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
归纳总结
3.菱形的判定:
有一组邻边相等的平行四边形叫做菱形
四条边都相等的四边形是菱形
对角线互相垂直的平行四边形是菱形.
方法1:
方法2:
方法3:
4.菱形是轴对称图形,它的两条对角线所在的直线都是它的对称轴,每条对角线平分一组对角.
即学即练
2.如图,在菱形ABCD中,对角线AC=10,BD=6,则菱形ABCD的面积为______.
30
A
B
C
O
D
1.如图,已知菱形的两条对角线长分别为6cm和8cm,则这个菱形的高DE为( )
A.2.4cm B.4.8cm C.5cm D.9.6cm
B
即学即练
3.如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE∥BD,过点D作ED∥AC,两线相交于点E.
求证:四边形AODE是菱形;
证明:∵AE∥BD,ED∥AC,
∴四边形AODE是平行四边形.
∵四边形ABCD是矩形,
∴AC=BD,OA=OC= AC,OB=OD= BD,
∴OA=OC=OD,
∴四边形AODE是菱形;
即学即练
解:(1)证明:由尺规作∠BAF的平分线的过程可得AB=AF,∠BAE=∠FAE,
∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠FAE=∠AEB,
∴∠BAE=∠AEB,∴AB=BE,
∴BE=FA,∴四边形ABEF为平行四边形,
∵AB=AF,∴四边形ABEF为菱形.
4.如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E,连接EF.
(1)求证:四边形ABEF为菱形;
即学即练
解:∵四边形ABEF为菱形,
∴AE⊥BF,BO= FB=3,AE=2AO,
在Rt△AOB中,由勾股定理得AO =4,
∴AE=2AO=8.
4.如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E,连接EF.
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.
归纳总结
正方形的性质及判定
1.定义:有一组邻边相等并且有一个角是直角的平行四边形叫正方形.
2.正方形的性质
正方形的四个角都是直角;
正方形的四条边都相等;
正方形的对角线相等,并且互相垂直平分;
正方形是轴对称图形,它有四条对称轴.
归纳总结
正方形
矩形
有一组邻边相等
菱形
有一个角是直角
有一组邻边相等
且有一个角是直角
3.正方形常见的判定方法
先证是矩形再证是菱形或先证是菱形再证是矩形
平行四边形
即学即练
2.如图,在正方形ABCD中,点E,H,F,G分别在边AB,BC,CD,DA上,EF,GH交于点O,∠FOH=90°, EF=4.则GH的长为 .
4
M
N
1.在正方形ABCD中,E是对角线AC上一点,且AE=AB,则∠EBC的度数是 .
A
D
B
C
O
E
22.5°
即学即练
3.如图,在四边形ABCD中, AB=BC ,对角线BD平分 ABC , P是BD上一点,过点P作PM AD , PN CD ,垂足分别为M、N.
(1) 求证: ADB= CDB;
C
A
B
D
P
M
N
证明:(1)∵BD平分∠ABC.
∴∠1=∠2.
又∵AB = BC,
∴△ABD≌△CBD (SAS).
∴∠ADB=∠CDB.
1
2
C
A
B
D
P
M
N
(2)∵PM⊥AD,PN⊥CD,∴∠PMD=∠PND=90°.
又∵∠ADC=90°,∴四边形NPMD是矩形.
∵∠ADB=∠CDB,
∴∠ADB=∠CDB=45°.
∴∠MPD=∠NPD=45°.
∴DM=PM,DN=PN.
∴四边形NPMD是正方形.
3.如图,在四边形ABCD中, AB=BC ,对角线BD平分 ABC , P是BD上一点,过点P作PM AD , PN CD ,垂足分别为M、N.
(2) 若 ADC=90 ,求证:四边形MPND是正方形.
即学即练
归纳总结
几种特殊四边形的性质汇总
项目 四边形 边 角 对角线 对称性
对边平行且相等
对边平行且相等
对边平行
且四边相等
对边平行
且四边相等
对角相等
四个角
都是直角
对角相等
四个角
都是直角
互相平分
互相平分且相等
互相垂直平分且相等,每一条对角线平分一组对角
轴对称图形
轴对称图形
轴对称图形
互相垂直且平分,每一条对角线平分一组对角
归纳总结
四边形 条件
几种特殊四边形的常用判定方法汇总:
1.定义:两组对边分别平行 2.两组对边分别相等
3.两组对角分别相等 4.对角线互相平分
5.一组对边平行且相等
1.定义:有一个角是直角的平行四边形
2.对角线相等的平行四边形
3.有三个角是直角的四边形
1.定义:一组邻边相等的平行四边形 ;2.对角线互相垂直的平行四边形,3.四条边都相等的四边形
1.定义:一组邻边相等且有一个角是直角的平行四边形
2.有一组邻边相等的矩形 3.有一个角是直角的菱形
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
