北京版九年级数学下册26.1一次函数与反比例函数的综合应用 教学设计(表格式)
文档属性
| 名称 | 北京版九年级数学下册26.1一次函数与反比例函数的综合应用 教学设计(表格式) |
|
|
| 格式 | doc | ||
| 文件大小 | 121.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-14 00:00:00 | ||
图片预览


文档简介
一次函数与反比例函数的综合应用
教学目标
进一步理解函数与方程、不等式之间的内在联系,应用函数图象比较两个函数的函数值的大小.在分析、归纳、解决问题的过程中,分析错因找出知识遗漏并梳理解决问题的思路,体会数形结合思想,提高分析问题解决问题的能力.在小组合作学习的过程中,增强合作意识和交流能力.
教学重难点
教学重点:应用函数图象解决比较两个函数的函数值大小的问题教学难点:解题思路的构建
教学过程
教学阶段 教师活动 学生活动 设置意图
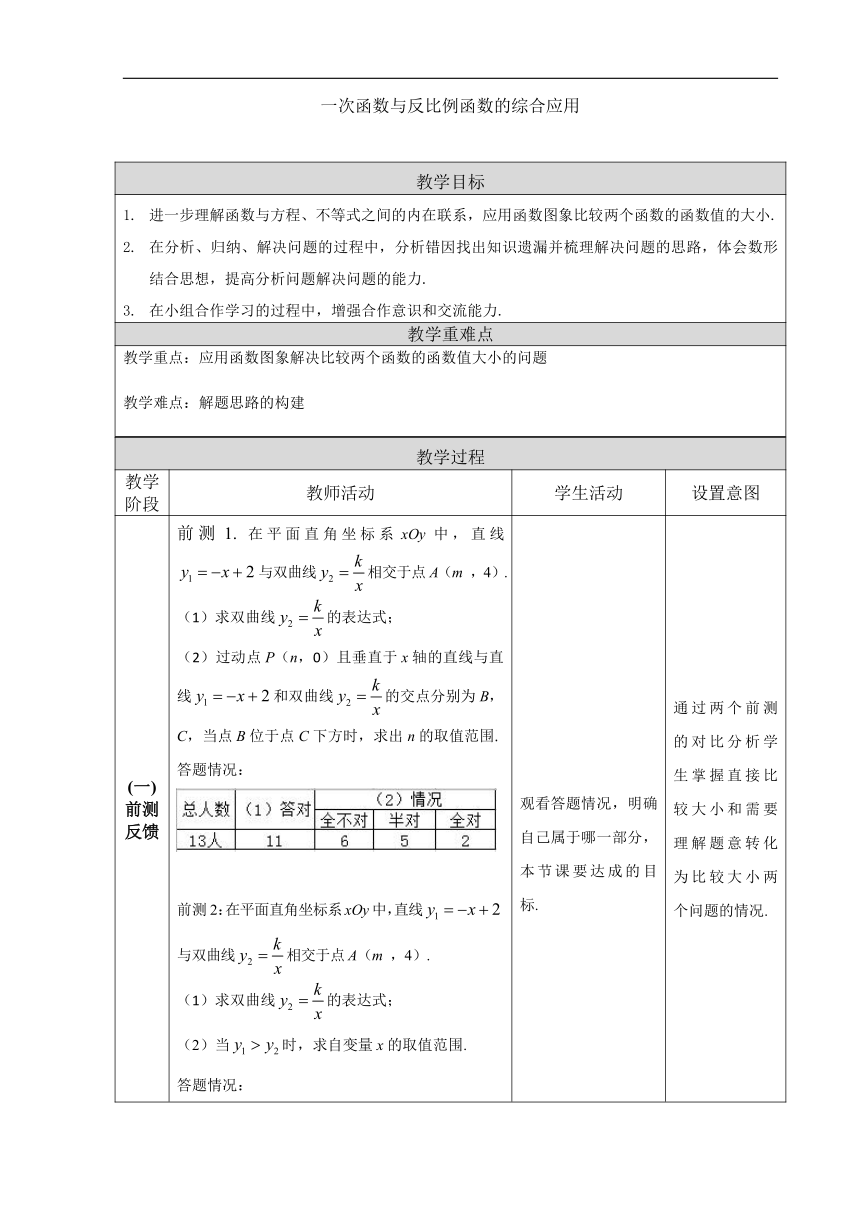
(一)前测反馈 前测1. 在平面直角坐标系xOy中,直线与双曲线相交于点A(m ,4).(1)求双曲线的表达式;(2)过动点P(n,0)且垂直于x轴的直线与直线和双曲线的交点分别为B,C,当点B位于点C下方时,求出n的取值范围.答题情况:前测2:在平面直角坐标系xOy中,直线与双曲线相交于点A(m ,4).(1)求双曲线的表达式;(2)当时,求自变量x的取值范围.答题情况:全班共13人,其中学困生3人,第一问的问题并不大,学困生中的两人计算出错.对于第二问,通过两个前测的对比,有四人对于直接比较大小的题目能够进行分析,得出一部分答案,对于前测1则无法理解题意,转化为比较大小的问题.本节课共需要解决两个问题:函数比较大小问题分析题目、准确理解题意,转化为函数比较大小问题. 观看答题情况,明确自己属于哪一部分,本节课要达成的目标.根据题目难易程度整合问题,明确本节课需要解决的问题. 通过两个前测的对比分析学生掌握直接比较大小和需要理解题意转化为比较大小两个问题的情况.明确本节课要解决的问题.
(二)问题解决 (一)解决问题——函数比较大小问题1.明确问题:两个函数比较大小.当x在什么范围内时,一次函数的函数值大于反比例函数的函数值.2.解决问题:(1)小组讨论:①对的同学分享自己解题的方法.②在组内分析自己的错因,共同找到解决的方法.(2)全班展示①讲解题目的解题方法.②展示组内出现的错因,并提供解决办法.(3)教师小结①为什么要借助函数图象来比较大小?②为什么要过两个函数的交点作垂直于x轴的直线?③为什么把y轴作为分界线?练习: 不等式 若,则x的取的解集为__________. 值范围是____________.④你能梳理一下解决这类问题的思路或步骤吗?(二)解决问题——理解题意1.展示学生的障碍点.(1)P(n,0)(引申(0,n)、(n、n)的含义)(2)点B位于点C下方2.画图、分析理解题意 把题目转化为:当时,求n的取值范围.3.完善思路4.提出问题小组讨论:类比以上两个问题,你还能提出其他的问题吗?独立思考:把题目写下来,注意标号.小组交流:辨析、整合题目,重新标号.全班展示:展示本组讨论的结果.预案: ③ 点B位于点C的上方.过点P(0,n)作直线l,使直线l与x轴平行.直线l与直线和双曲线分别交于M、N两点,当点M位于点N左边时,求出n的取值范围. 小结:不同的问法,实质都是已知两个函数的大小关系求自变量的取值范围.应用总结的思路均可解决此类问题. 明确问题的具体含义小组合作展示思考问题小组讨论练习自己梳理,进而完善思考问题自己画图,理解题意完善解题思路独立思考、小组交流、全班展示 通过伙伴互助解决自己的问题,分析错因找出遗漏的知识.通过对三个问题的思考深入理解利用函数图象比较函数值大小的原因及方法.通过两个简单的小练习检测学生掌握的情况通过对思路步骤的梳理提升对这一类问题的认识,找到解决这一类问题的方法.通过对于障碍点的分析解决学生在解题过程中出现的难点,从而把较难问题转化为简单问题.通过完善思路再次明确解决问题的思想和方法发散思维,通过自己提出问题进一步理解这一类问题的本质,从而应用解题策略解决此类问题.
(三)反思小结 师生共同总结本节课的收获与体会。1.知识:利用函数图象来解决比较两个函数的函数值大小的问题2.数学思想和方法:(1)解题思路(2)数形结合思想、转化思想 畅谈收获与体会 通过师生的共同回忆、总结,达到知识、能力的再提升.
(四)布置作业
PAGE
教学目标
进一步理解函数与方程、不等式之间的内在联系,应用函数图象比较两个函数的函数值的大小.在分析、归纳、解决问题的过程中,分析错因找出知识遗漏并梳理解决问题的思路,体会数形结合思想,提高分析问题解决问题的能力.在小组合作学习的过程中,增强合作意识和交流能力.
教学重难点
教学重点:应用函数图象解决比较两个函数的函数值大小的问题教学难点:解题思路的构建
教学过程
教学阶段 教师活动 学生活动 设置意图
(一)前测反馈 前测1. 在平面直角坐标系xOy中,直线与双曲线相交于点A(m ,4).(1)求双曲线的表达式;(2)过动点P(n,0)且垂直于x轴的直线与直线和双曲线的交点分别为B,C,当点B位于点C下方时,求出n的取值范围.答题情况:前测2:在平面直角坐标系xOy中,直线与双曲线相交于点A(m ,4).(1)求双曲线的表达式;(2)当时,求自变量x的取值范围.答题情况:全班共13人,其中学困生3人,第一问的问题并不大,学困生中的两人计算出错.对于第二问,通过两个前测的对比,有四人对于直接比较大小的题目能够进行分析,得出一部分答案,对于前测1则无法理解题意,转化为比较大小的问题.本节课共需要解决两个问题:函数比较大小问题分析题目、准确理解题意,转化为函数比较大小问题. 观看答题情况,明确自己属于哪一部分,本节课要达成的目标.根据题目难易程度整合问题,明确本节课需要解决的问题. 通过两个前测的对比分析学生掌握直接比较大小和需要理解题意转化为比较大小两个问题的情况.明确本节课要解决的问题.
(二)问题解决 (一)解决问题——函数比较大小问题1.明确问题:两个函数比较大小.当x在什么范围内时,一次函数的函数值大于反比例函数的函数值.2.解决问题:(1)小组讨论:①对的同学分享自己解题的方法.②在组内分析自己的错因,共同找到解决的方法.(2)全班展示①讲解题目的解题方法.②展示组内出现的错因,并提供解决办法.(3)教师小结①为什么要借助函数图象来比较大小?②为什么要过两个函数的交点作垂直于x轴的直线?③为什么把y轴作为分界线?练习: 不等式 若,则x的取的解集为__________. 值范围是____________.④你能梳理一下解决这类问题的思路或步骤吗?(二)解决问题——理解题意1.展示学生的障碍点.(1)P(n,0)(引申(0,n)、(n、n)的含义)(2)点B位于点C下方2.画图、分析理解题意 把题目转化为:当时,求n的取值范围.3.完善思路4.提出问题小组讨论:类比以上两个问题,你还能提出其他的问题吗?独立思考:把题目写下来,注意标号.小组交流:辨析、整合题目,重新标号.全班展示:展示本组讨论的结果.预案: ③ 点B位于点C的上方.过点P(0,n)作直线l,使直线l与x轴平行.直线l与直线和双曲线分别交于M、N两点,当点M位于点N左边时,求出n的取值范围. 小结:不同的问法,实质都是已知两个函数的大小关系求自变量的取值范围.应用总结的思路均可解决此类问题. 明确问题的具体含义小组合作展示思考问题小组讨论练习自己梳理,进而完善思考问题自己画图,理解题意完善解题思路独立思考、小组交流、全班展示 通过伙伴互助解决自己的问题,分析错因找出遗漏的知识.通过对三个问题的思考深入理解利用函数图象比较函数值大小的原因及方法.通过两个简单的小练习检测学生掌握的情况通过对思路步骤的梳理提升对这一类问题的认识,找到解决这一类问题的方法.通过对于障碍点的分析解决学生在解题过程中出现的难点,从而把较难问题转化为简单问题.通过完善思路再次明确解决问题的思想和方法发散思维,通过自己提出问题进一步理解这一类问题的本质,从而应用解题策略解决此类问题.
(三)反思小结 师生共同总结本节课的收获与体会。1.知识:利用函数图象来解决比较两个函数的函数值大小的问题2.数学思想和方法:(1)解题思路(2)数形结合思想、转化思想 畅谈收获与体会 通过师生的共同回忆、总结,达到知识、能力的再提升.
(四)布置作业
PAGE
