北京版九年级数学下册 对称性质在折叠问题中的应用 教学设计
文档属性
| 名称 | 北京版九年级数学下册 对称性质在折叠问题中的应用 教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 200.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-14 00:00:00 | ||
图片预览


文档简介
《对称性质在折叠问题中的应用》教学设计
教学目标
知识与技能:
1.掌握折叠问题的方法;
2.掌握折叠问题中求角度和求线段长的方法。
过程与方法:
1、 通过探究和推理论证,发展学生的分析问题和解决问题的能力;
2、 通过经历矩形折叠问题的探究,掌握探究问题的方法;
3、 体会利用方程思想、转化思想解决折叠问题的一般方法.
情感态度价值观:
提供探究问题的机会,让学生体验数学活动中充满着探索与创新,激发学生学习几何的兴趣,获得解决问题的成功体验。
教学重难点
熟练掌握矩形折叠问题中求角度和求线段长的方法。
模型1:将矩形ABCD沿CF折叠,使E落在AB上
折叠图形 图形分析及所得结论
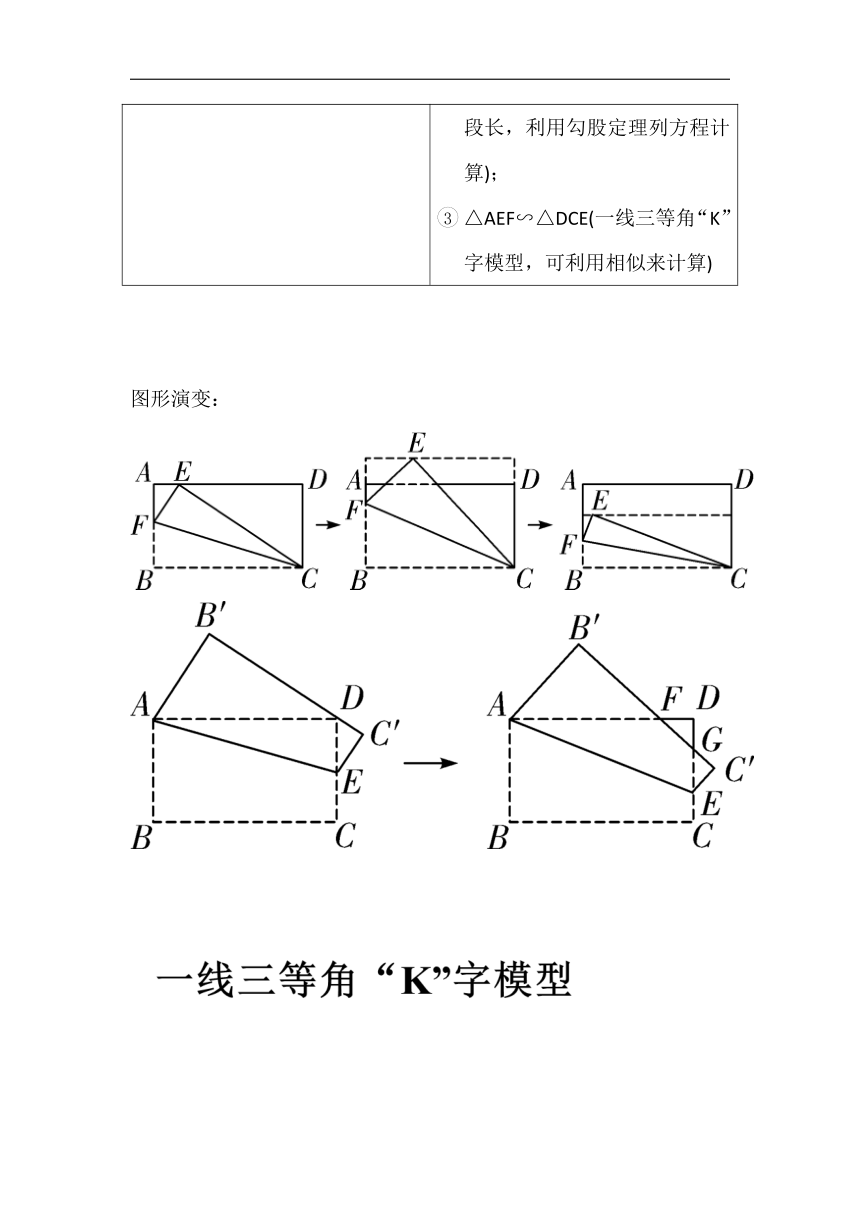
BCF≌△ECF;△BCF、△ECF、△AFE、△EDC为直角三角形(可利用对应边,对应角相等转移条件,表示线段长,利用勾股定理列方程计算);△AEF∽△DCE(一线三等角“K”字模型,可利用相似来计算)
图形演变:
课堂练习:
1. 如图,折叠长方形的边AD,使点D落在BC边上的点F处,若AB=4 cm,BC=5 cm,则EF的长为______ cm.
2. 如图,在矩形纸片ABCD中,已知AB=1,BC= ,点E在边CD上移动,连接AE,将多边形ABCE沿直线AE翻折,得到多边形AB′C′E,点B、C的对应点分别为点B′、C′.
(1)如图①,当B′C′恰好经过点D时,求线段CE的长;
(2)如图②,若B′C′分别交边AD,CD于点F,G,
且∠DAE=22.5°,求△DFG的面积.
模型2:将矩形ABCD沿对角线BD折叠,点C的对应点记为C′,C′B交AD于点E
折叠图形 图形分析及所得结论
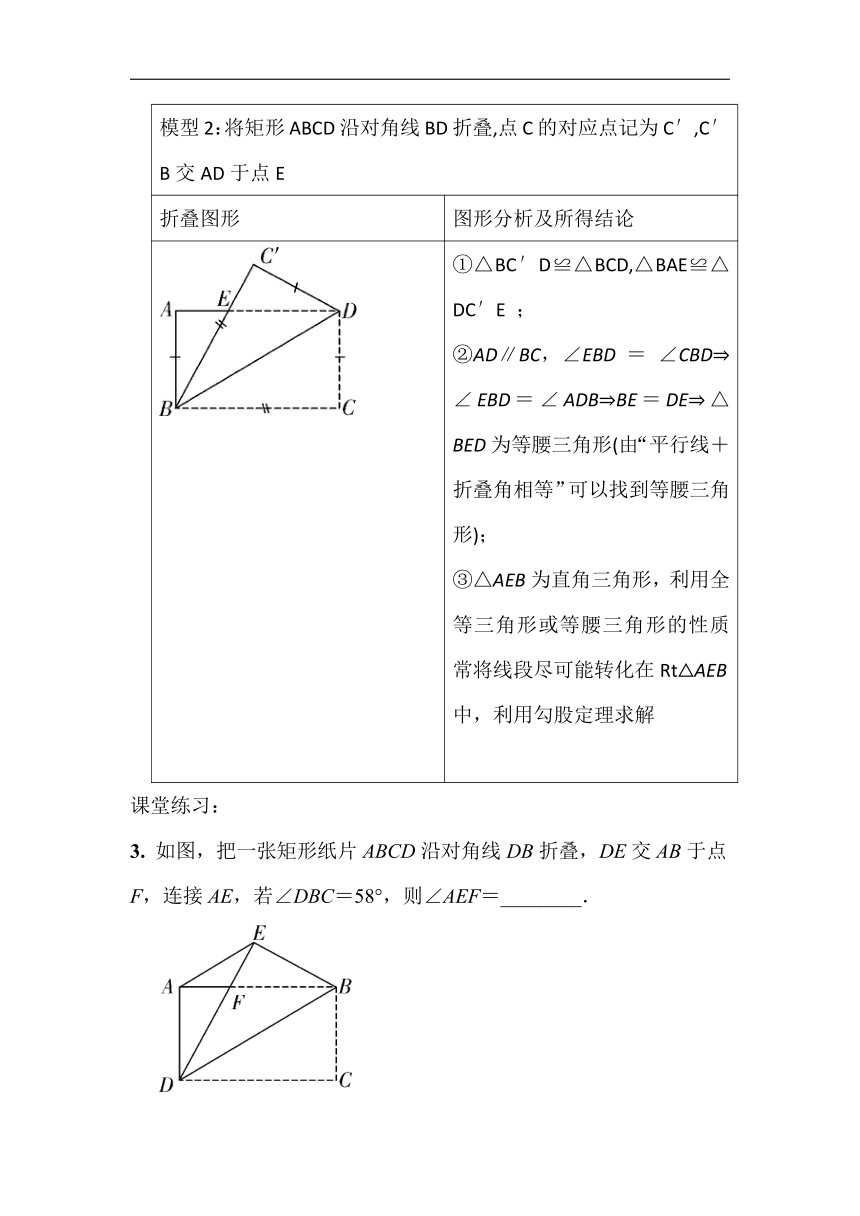
①△BC′D≌△BCD,△BAE≌△DC′E ;②AD∥BC,∠EBD = ∠CBD ∠EBD=∠ADB BE=DE △BED为等腰三角形(由“平行线+折叠角相等”可以找到等腰三角形);③△AEB为直角三角形,利用全等三角形或等腰三角形的性质常将线段尽可能转化在Rt△AEB中,利用勾股定理求解
课堂练习:
3. 如图,把一张矩形纸片ABCD沿对角线DB折叠,DE交AB于点F,连接AE,若∠DBC=58°,则∠AEF=________.
模型3:将矩形ABCD沿EF折叠,使点E、F分别为AD、BC上的点
折叠图形 图形分析及所得结论
BF=B′F,∠BFE=∠B′FE;角平分线遇平行线时出现等腰三角形 B′E=B′F,△B′EF为等腰三角形;对称点的连线被对称轴垂直平分 折痕EF垂直平分BB′,可知四边形EB′FB为菱形;△A′B′E是直角三角形,利用等腰三角形、垂直平分线的性质将线段转化在Rt△A′B′E中,利用勾股定理求解
图形演变
课堂练习:
4. 在矩形纸片ABCD中,AB=3 cm,BC=4 cm,
现将纸片折叠压平,使点C与点A重合,设折痕
为EF,则重叠部分△AEF的面积等于_____ cm2.
5. (2018年广西北部湾经济区)如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE,DE分别交AB于点O,F,且OP=OF,则cos∠ADF的值为( )
课堂小结:
一、图形折叠问题中题型的变化比较多,主要有以下几点: 1.图形的翻折部分在折叠前和折叠后的形状、大小不变,是全等形;
2.图形的翻折部分在折叠前和折叠后的位置关于折痕成轴对称;
3.将长方形纸片折叠,三角形是否为等腰三角形; 4.解决折叠问题时,要抓住图形之间最本质的位置关系,从而进一步发现其中的数量关系;
5.充分挖掘图形的几何性质,将其中的基本的数量关系,用方程的形式表达出来(勾股定理,相似三角形),并迅速求解,这是解题时常用的方法之一。
二:折叠问题数学思想:
(1)思考问题的逆向(反方向);
(2)从一般问题的特例人手,寻找问题解决的思路; (3)把一个复杂问题转化为解决过的基本问题的转化与化归思想;
(4)归纳与分类的思想(把折纸中发现的诸多关系归纳出来,并进行分类);
(5)从变化中寻找不变性的思想.用“操作”、“观察”、“猜想”、“分析”的手段去感悟几何图形的性质是学习几何的方法。
布置作业:
同步学习:P62第14题,第15题。
教学目标
知识与技能:
1.掌握折叠问题的方法;
2.掌握折叠问题中求角度和求线段长的方法。
过程与方法:
1、 通过探究和推理论证,发展学生的分析问题和解决问题的能力;
2、 通过经历矩形折叠问题的探究,掌握探究问题的方法;
3、 体会利用方程思想、转化思想解决折叠问题的一般方法.
情感态度价值观:
提供探究问题的机会,让学生体验数学活动中充满着探索与创新,激发学生学习几何的兴趣,获得解决问题的成功体验。
教学重难点
熟练掌握矩形折叠问题中求角度和求线段长的方法。
模型1:将矩形ABCD沿CF折叠,使E落在AB上
折叠图形 图形分析及所得结论
BCF≌△ECF;△BCF、△ECF、△AFE、△EDC为直角三角形(可利用对应边,对应角相等转移条件,表示线段长,利用勾股定理列方程计算);△AEF∽△DCE(一线三等角“K”字模型,可利用相似来计算)
图形演变:
课堂练习:
1. 如图,折叠长方形的边AD,使点D落在BC边上的点F处,若AB=4 cm,BC=5 cm,则EF的长为______ cm.
2. 如图,在矩形纸片ABCD中,已知AB=1,BC= ,点E在边CD上移动,连接AE,将多边形ABCE沿直线AE翻折,得到多边形AB′C′E,点B、C的对应点分别为点B′、C′.
(1)如图①,当B′C′恰好经过点D时,求线段CE的长;
(2)如图②,若B′C′分别交边AD,CD于点F,G,
且∠DAE=22.5°,求△DFG的面积.
模型2:将矩形ABCD沿对角线BD折叠,点C的对应点记为C′,C′B交AD于点E
折叠图形 图形分析及所得结论
①△BC′D≌△BCD,△BAE≌△DC′E ;②AD∥BC,∠EBD = ∠CBD ∠EBD=∠ADB BE=DE △BED为等腰三角形(由“平行线+折叠角相等”可以找到等腰三角形);③△AEB为直角三角形,利用全等三角形或等腰三角形的性质常将线段尽可能转化在Rt△AEB中,利用勾股定理求解
课堂练习:
3. 如图,把一张矩形纸片ABCD沿对角线DB折叠,DE交AB于点F,连接AE,若∠DBC=58°,则∠AEF=________.
模型3:将矩形ABCD沿EF折叠,使点E、F分别为AD、BC上的点
折叠图形 图形分析及所得结论
BF=B′F,∠BFE=∠B′FE;角平分线遇平行线时出现等腰三角形 B′E=B′F,△B′EF为等腰三角形;对称点的连线被对称轴垂直平分 折痕EF垂直平分BB′,可知四边形EB′FB为菱形;△A′B′E是直角三角形,利用等腰三角形、垂直平分线的性质将线段转化在Rt△A′B′E中,利用勾股定理求解
图形演变
课堂练习:
4. 在矩形纸片ABCD中,AB=3 cm,BC=4 cm,
现将纸片折叠压平,使点C与点A重合,设折痕
为EF,则重叠部分△AEF的面积等于_____ cm2.
5. (2018年广西北部湾经济区)如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE,DE分别交AB于点O,F,且OP=OF,则cos∠ADF的值为( )
课堂小结:
一、图形折叠问题中题型的变化比较多,主要有以下几点: 1.图形的翻折部分在折叠前和折叠后的形状、大小不变,是全等形;
2.图形的翻折部分在折叠前和折叠后的位置关于折痕成轴对称;
3.将长方形纸片折叠,三角形是否为等腰三角形; 4.解决折叠问题时,要抓住图形之间最本质的位置关系,从而进一步发现其中的数量关系;
5.充分挖掘图形的几何性质,将其中的基本的数量关系,用方程的形式表达出来(勾股定理,相似三角形),并迅速求解,这是解题时常用的方法之一。
二:折叠问题数学思想:
(1)思考问题的逆向(反方向);
(2)从一般问题的特例人手,寻找问题解决的思路; (3)把一个复杂问题转化为解决过的基本问题的转化与化归思想;
(4)归纳与分类的思想(把折纸中发现的诸多关系归纳出来,并进行分类);
(5)从变化中寻找不变性的思想.用“操作”、“观察”、“猜想”、“分析”的手段去感悟几何图形的性质是学习几何的方法。
布置作业:
同步学习:P62第14题,第15题。
