沪科版数学八年级下册 19.1 多边形内角和 课件(共31张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 19.1 多边形内角和 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 729.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-14 00:00:00 | ||
图片预览







文档简介
(共31张PPT)
19.1 多边形内角和
生活中的平面图形
由这图形你抽象出什么几何图形?
三角形
在平面内,由三条不在同一直线上的线段首尾顺次相接组成的封闭图形
在平面内,由四条不在同一直线上的线段首尾顺次相接组成的封闭图形,记为四边形ABCD
四边形
A
D
B
C
在平面内,由五条不在同一直线上的线段首尾顺次相接组成的封闭图形,记为五边形ABCDE
A
E
D
C
B
生活中的平面图形
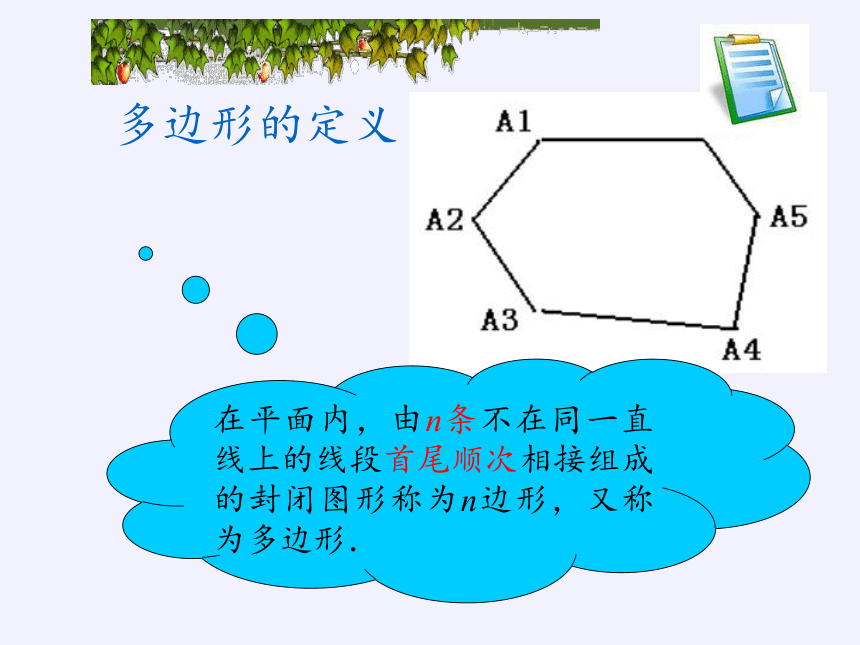
在平面内,由n条不在同一直线上的线段首尾顺次相接组成的封闭图形称为n边形,又称为多边形.
多边形的定义
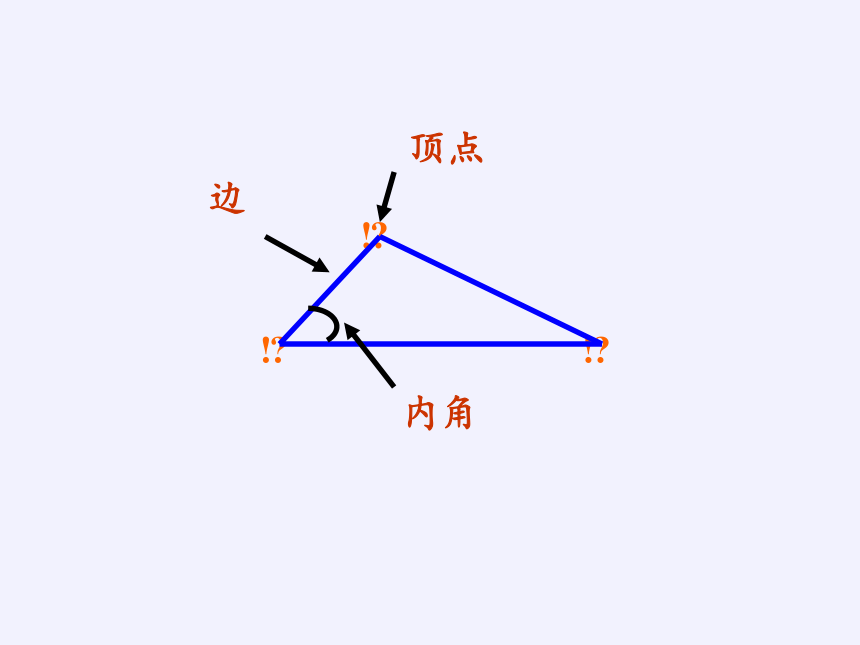
顶点
边
内角
顶点
内角
边
对角线
(连接不相邻两个顶点的线段)
多边形的相关元素
外角
A
C
B
D
E
一个n 边形有 个顶点, 条边, 个内角, 个外角,从一个顶点出发,最多能引 条对角线。
n
n
n
n
n - 3
三角形如果三条边都相等,三个角也都相等,那么这样的三角形就叫做正三角形.
如果多边形各边都相等,各个角也都相等,那么这样的多边形就叫做正多边形.如正三角形、正四边形(正方形)、正五边形等等 .
正多边形
下列图形是不是正多边形?
菱形
长方形
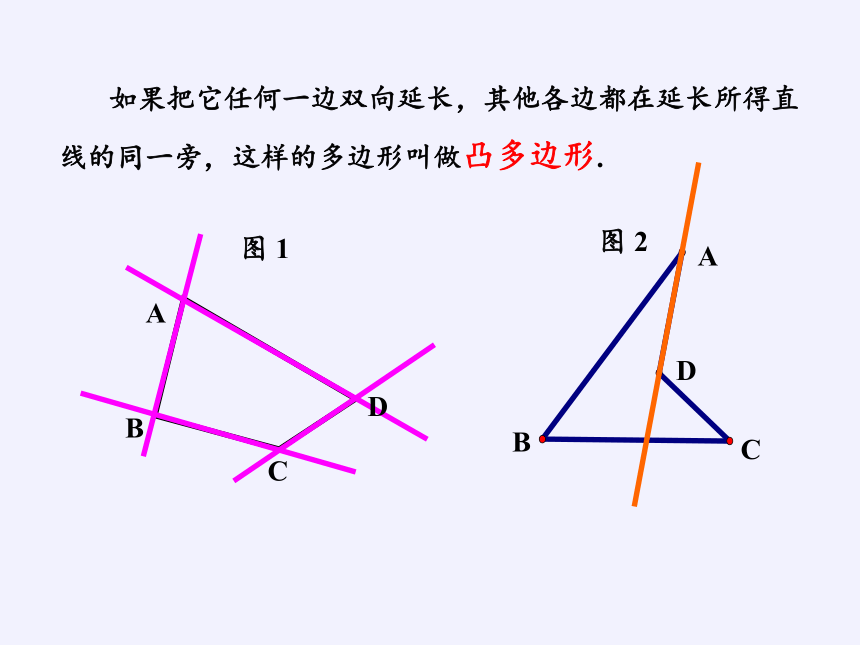
图 2
如果把它任何一边双向延长,其他各边都在延长所得直线的同一旁,这样的多边形叫做凸多边形.
图 1
A
C
B
D
A
C
B
D
⑴我们知道三角形内角和是多少?
与形状、大小有关吗?
动手操作,探索新知:
活动1: 探究多边形内角和
(2)长方形、正方形的内角和是多少?
4×90°=360°
能猜想任意凸四边形内角和吗?
A
B
C
D
A
D
B
C
方法一:
D
B
C
A
D
B
四边形内角和: 2×180°=360°
课堂导学
A
B
C
D
方法二:
四边形内角和:3×180°-180°
1
2
3
1
2
3
B
C
A
D
方法三:
四边形内角和等于4×180°-360°
1
2
3
4
2
1
3
4
A
D
B
C
D
B
C
A
D
B
A
B
C
D
1
2
3
1
2
3
B
C
A
D
1
2
3
4
2
1
3
4
方法一:由多边形一个顶点引对角线分割三角形
方法二:在多边形一条边上任取一点分割三角形
方法三:在多边形内部任取一点分割三角形
多边形 三角形 四边形 五边形 六边形 … n边形
从一个点出发引对角线的条数
分割成三角形的个数
内角和
1
2
3
4
n-2
…
…
180°
2×180°
3×180°
4×180°
(n-2)×180°
…
0
1
2
3
n-3
按照第一种分割的做法来看:
多边形的边数每多一条,它的内角和就增加 .
180°
归纳
n边形内角和公式
n边形的内角和等于(n-2)×180°
n是大于或等于3的正整数
说明:多边形的内角和仅与边数有关,与多边形的大小、形状无关.
练一练 看谁又快又准
1、12边形的内角和等于_______
2、如果一个多边形的内角和等于1440°,那么这是___边形
1800°
十
已知边数求多边形内角和
已知多边形内角和求边数
解:由多边形的内角和公式可得:
(12-2)×180°=1800°
解:设这个多边形是n边形,由多边 形的内角和公式可得:
(n-2)×180°=1440°
n=10
3、若n边形的内角和是144n°,那么n=
10
解:由多边形的内角和公式可得:
(n - 2) · 180° = 144n°
n = 10
4 、已知一个多边形的每一个内角都是156°,则它的边数为__.
15
解:设这个多边形是n边形,由多边形的内角和公式可得:
(n - 2)· 180° = 156n°
n = 15
提升练习
在四边形ABCD中,∠A=120°,∠B:∠C:∠D = 3:4:5.求∠B,∠C,∠D的度数。
解:设∠B,∠C,∠D的度数分别是3x, 4x , 5x 度,由四边形的内角和等于360°可得:
120 + 3x + 4x +5x = 360
整理,得 12x = 240
解方程,得 x = 20
∴ 3x = 60
4x = 80
5x = 100
答:∠B,∠C,∠D分别为60°,80°, 100°.
有一张长方形的桌面,现在锯掉它的一个角,有几种情况?剩下的残余桌面的内角和为多少?
思考题:
三角形的外角和是多少度?你是怎样探究出来的?
A
B
C
D
E
F
1.先把三角形的三个外角和三个内角这六个角
的和求出来,刚好是三个平角.
2.再用这六个角的和减去三个内角的和,剩下
的就是三角形的外角和了!
3×1800-(3-2) ×1800=3600
活动2:探究多边形的外角和
那么你能研究出四边形的外角和吗?
4× 180°-(4-2) × 180°= 360°
类比推理
五边形的外角和是多少度?
六边形的外角和是多少度?
n边形的外角和是多少度?
… … … … … … …
5×1800-(5-2) ×1800=3600
6×1800-(6-2) ×1800=3600
n×1800-(n-2) ×1800=
3600
n边形的内角和等于(n-2)·180 (n为不小于3的整数)
n边形的外角和等于360
例题:一个多边形的内角和等于它的外角和的3倍,它是几边形?
解:设这个多边形是n边形,则它的内角和是(n-2)·180°,外角和等于360°,
所以:(n-2)·180=3×360
解得: n = 8
答:这个多边形是八边形.
练一练
1、如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____。
12
n×30°=360°
n=12
解:设这个多边形是n边形 。 n边形外角和=360 °
练一练
2、正五边形的每一个外角等于____,每一个内角等于_____。
5X=360°
X=72°
72°
108°
解:设正五边形的每一个外角度数为x,由
多边形的外角和等于360度可得:
所以每一个内角度数为108 °
课堂小结
在平面内,由若干条不在同一条直线上的线段首尾顺次相接组成的封闭图形叫做多边形.
n边形的内角和等于(n-2)·180 (n为不小于3的整数)
说明:多边形的内角和仅与边数有关,与多边形的大小、形状无关.
n边形的外角和等于360
方法:
类比,转化,归纳
谢 谢
19.1 多边形内角和
生活中的平面图形
由这图形你抽象出什么几何图形?
三角形
在平面内,由三条不在同一直线上的线段首尾顺次相接组成的封闭图形
在平面内,由四条不在同一直线上的线段首尾顺次相接组成的封闭图形,记为四边形ABCD
四边形
A
D
B
C
在平面内,由五条不在同一直线上的线段首尾顺次相接组成的封闭图形,记为五边形ABCDE
A
E
D
C
B
生活中的平面图形
在平面内,由n条不在同一直线上的线段首尾顺次相接组成的封闭图形称为n边形,又称为多边形.
多边形的定义
顶点
边
内角
顶点
内角
边
对角线
(连接不相邻两个顶点的线段)
多边形的相关元素
外角
A
C
B
D
E
一个n 边形有 个顶点, 条边, 个内角, 个外角,从一个顶点出发,最多能引 条对角线。
n
n
n
n
n - 3
三角形如果三条边都相等,三个角也都相等,那么这样的三角形就叫做正三角形.
如果多边形各边都相等,各个角也都相等,那么这样的多边形就叫做正多边形.如正三角形、正四边形(正方形)、正五边形等等 .
正多边形
下列图形是不是正多边形?
菱形
长方形
图 2
如果把它任何一边双向延长,其他各边都在延长所得直线的同一旁,这样的多边形叫做凸多边形.
图 1
A
C
B
D
A
C
B
D
⑴我们知道三角形内角和是多少?
与形状、大小有关吗?
动手操作,探索新知:
活动1: 探究多边形内角和
(2)长方形、正方形的内角和是多少?
4×90°=360°
能猜想任意凸四边形内角和吗?
A
B
C
D
A
D
B
C
方法一:
D
B
C
A
D
B
四边形内角和: 2×180°=360°
课堂导学
A
B
C
D
方法二:
四边形内角和:3×180°-180°
1
2
3
1
2
3
B
C
A
D
方法三:
四边形内角和等于4×180°-360°
1
2
3
4
2
1
3
4
A
D
B
C
D
B
C
A
D
B
A
B
C
D
1
2
3
1
2
3
B
C
A
D
1
2
3
4
2
1
3
4
方法一:由多边形一个顶点引对角线分割三角形
方法二:在多边形一条边上任取一点分割三角形
方法三:在多边形内部任取一点分割三角形
多边形 三角形 四边形 五边形 六边形 … n边形
从一个点出发引对角线的条数
分割成三角形的个数
内角和
1
2
3
4
n-2
…
…
180°
2×180°
3×180°
4×180°
(n-2)×180°
…
0
1
2
3
n-3
按照第一种分割的做法来看:
多边形的边数每多一条,它的内角和就增加 .
180°
归纳
n边形内角和公式
n边形的内角和等于(n-2)×180°
n是大于或等于3的正整数
说明:多边形的内角和仅与边数有关,与多边形的大小、形状无关.
练一练 看谁又快又准
1、12边形的内角和等于_______
2、如果一个多边形的内角和等于1440°,那么这是___边形
1800°
十
已知边数求多边形内角和
已知多边形内角和求边数
解:由多边形的内角和公式可得:
(12-2)×180°=1800°
解:设这个多边形是n边形,由多边 形的内角和公式可得:
(n-2)×180°=1440°
n=10
3、若n边形的内角和是144n°,那么n=
10
解:由多边形的内角和公式可得:
(n - 2) · 180° = 144n°
n = 10
4 、已知一个多边形的每一个内角都是156°,则它的边数为__.
15
解:设这个多边形是n边形,由多边形的内角和公式可得:
(n - 2)· 180° = 156n°
n = 15
提升练习
在四边形ABCD中,∠A=120°,∠B:∠C:∠D = 3:4:5.求∠B,∠C,∠D的度数。
解:设∠B,∠C,∠D的度数分别是3x, 4x , 5x 度,由四边形的内角和等于360°可得:
120 + 3x + 4x +5x = 360
整理,得 12x = 240
解方程,得 x = 20
∴ 3x = 60
4x = 80
5x = 100
答:∠B,∠C,∠D分别为60°,80°, 100°.
有一张长方形的桌面,现在锯掉它的一个角,有几种情况?剩下的残余桌面的内角和为多少?
思考题:
三角形的外角和是多少度?你是怎样探究出来的?
A
B
C
D
E
F
1.先把三角形的三个外角和三个内角这六个角
的和求出来,刚好是三个平角.
2.再用这六个角的和减去三个内角的和,剩下
的就是三角形的外角和了!
3×1800-(3-2) ×1800=3600
活动2:探究多边形的外角和
那么你能研究出四边形的外角和吗?
4× 180°-(4-2) × 180°= 360°
类比推理
五边形的外角和是多少度?
六边形的外角和是多少度?
n边形的外角和是多少度?
… … … … … … …
5×1800-(5-2) ×1800=3600
6×1800-(6-2) ×1800=3600
n×1800-(n-2) ×1800=
3600
n边形的内角和等于(n-2)·180 (n为不小于3的整数)
n边形的外角和等于360
例题:一个多边形的内角和等于它的外角和的3倍,它是几边形?
解:设这个多边形是n边形,则它的内角和是(n-2)·180°,外角和等于360°,
所以:(n-2)·180=3×360
解得: n = 8
答:这个多边形是八边形.
练一练
1、如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____。
12
n×30°=360°
n=12
解:设这个多边形是n边形 。 n边形外角和=360 °
练一练
2、正五边形的每一个外角等于____,每一个内角等于_____。
5X=360°
X=72°
72°
108°
解:设正五边形的每一个外角度数为x,由
多边形的外角和等于360度可得:
所以每一个内角度数为108 °
课堂小结
在平面内,由若干条不在同一条直线上的线段首尾顺次相接组成的封闭图形叫做多边形.
n边形的内角和等于(n-2)·180 (n为不小于3的整数)
说明:多边形的内角和仅与边数有关,与多边形的大小、形状无关.
n边形的外角和等于360
方法:
类比,转化,归纳
谢 谢
