沪科版数学八年级下册 19.1多边形内角和 课件(共16张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 19.1多边形内角和 课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-14 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
沪科版本数学学科八年级下册第19章第一节
19.1 多边形内角和
19.1 多边形内角和
沪科版本数学学科八年级下册第19章第一节
19.1 多边形内角和
19.1 多边形内角和
19.1 多边形内角和
19.1 多边形内角和
沪科版本数学学科八年级下册第19章第一节
学习目标:
1.从特殊到一般的研究方法,探索n边形的内角和公式 ;
3. 会用转化思想进行多种方法解决问题.
2.运用多边形内角和公式进行相关计算;
19.1 多边形内角和
沪科版本数学学科八年级下册第19章第一节
轻松回忆:
2:长方形和正方形的内角和是多少度?
1:三角形内角和是多少度?
(三角形内角和 180°)
(都是360°)
19.1 多边形内角和
沪科版本数学学科八年级下册第19章第一节
你能猜吗:
任意一个四边形的内角和是多少度?
请你任意画一个四边形,用量角器量一下各个内角的度数,计算一下四边形的内角和。
动动手:
(360°)
(360°)
19.1 多边形内角和
沪科版本数学学科八年级下册第19章第一节
动脑思考:
方法一:如图所示,利用辅助线将四边形分割成两个三角形
你能证明四边形的内角和等于360 °吗?
四边形的内角和
= 两个三角形的内角和相加
= 180 °+ 180 °
= 360 °
解题思路:把四边形问题转化为三角形问题来解决
19.1 多边形内角和
沪科版本数学学科八年级下册第19章第一节
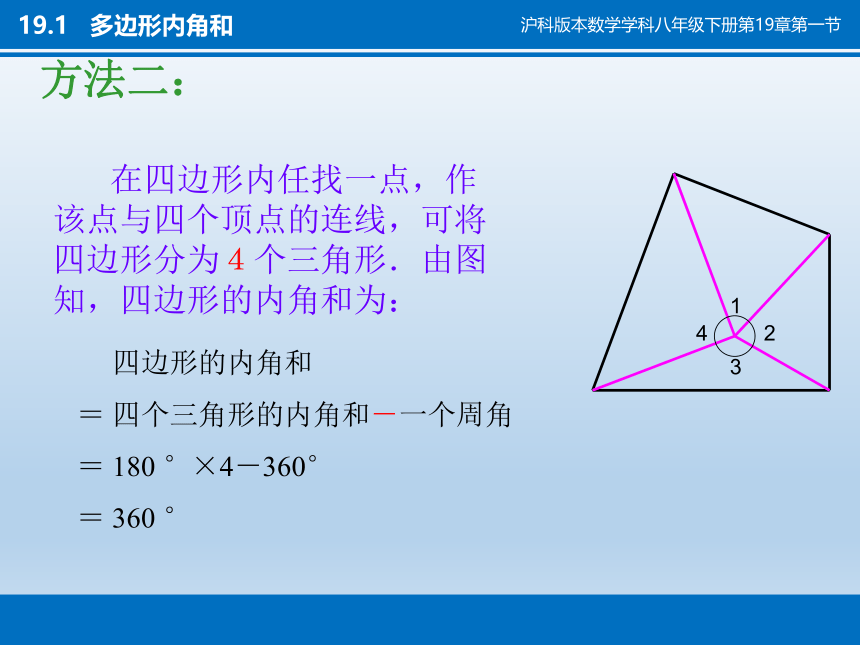
在四边形内任找一点,作该点与四个顶点的连线,可将四边形分为4个三角形.由图知,四边形的内角和为:
方法二:
1
2
3
4
四边形的内角和
= 四个三角形的内角和-一个周角
= 180 °×4-360°
= 360 °
19.1 多边形内角和
沪科版本数学学科八年级下册第19章第一节
在四边形一边上找一点,作该点与另两个顶点的连线,可将四边形分为3个三角形.由图知,四边形的内角和为:
180°×3- 180° =360°
方法三:
1
2
3
19.1 多边形内角和
沪科版本数学学科八年级下册第19章第一节
180°×3- 180° =360°
在四边形外部找一点,作该点与另四个顶点的连线.由图知,四边形的内角和为:
方法四:
1
2
19.1 多边形内角和
沪科版本数学学科八年级下册第19章第一节
请选择一种你喜欢的方法,试说明五边形、六边形的内角和
19.1 多边形内角和
沪科版本数学学科八年级下册第19章第一节
n边形的边数 3 4 5 6 7 … n
分成三角形的个数 …
多边形的内角和 …
1
180°
2
3
4
5
360°
540°
720°
900°
n-2
(n-2)×180°
探索多(n)边形的内角和
19.1 多边形内角和
沪科版本数学学科八年级下册第19章第一节
n边形的内角和等于 (n-2)×180°
由此等式我们可以知道:
已知多边形的边数可以求出它的内角和,反之,已知多边形的内角和也可以求出它的边数
19.1 多边形内角和
沪科版本数学学科八年级下册第19章第一节
学以致用
2、十边形的内角和是( );如果十边形的各个内角都相等,那么它的一个内角是( )
1、七边形内角和为( )
900°
1440 °
144°
分析:(n-2)×180°=(7-2)×180°=900°
分析:(n-2)×180°=(10-2)×180°=1440°
1440°÷10=144°
19.1 多边形内角和
沪科版本数学学科八年级下册第19章第一节
学以致用
3、多边形内角和为1080°则它是( )边形。
4、多边形内角和为1800°则它是( )边形。
八
十二
分析:设多边形的边数为n,由题意得:
(n-2)×180°=1080°
解这个方程得:n=8
分析:设多边形的边数为n,由题意得:
(n-2)×180°=1800°
解这个方程得:n=12
19.1 多边形内角和
沪科版本数学学科八年级下册第19章第一节
如果一个四边形的一组对角互补,那么另一组对角有什么关系?
解:如图,四边形ABCD中,∠A+∠C=180°。
∵∠A+∠B+∠C+∠D=(4-2)×360°=180
∴∠B+∠D= 360°-(∠A+∠C)=180°
这就是说:如果四边形一组对角互补,那么另一组对角也互补.
分析:如图,在四边形ABCD 中 ,要求∠B与∠D的关系,由于已知∠A+∠C=180°,所以可以从四边形的内角和入手,就可得到完满的答案.
加深理解
沪科版本数学学科八年级下册第19章第一节
19.1 多边形内角和
19.1 多边形内角和
沪科版本数学学科八年级下册第19章第一节
19.1 多边形内角和
19.1 多边形内角和
19.1 多边形内角和
19.1 多边形内角和
沪科版本数学学科八年级下册第19章第一节
学习目标:
1.从特殊到一般的研究方法,探索n边形的内角和公式 ;
3. 会用转化思想进行多种方法解决问题.
2.运用多边形内角和公式进行相关计算;
19.1 多边形内角和
沪科版本数学学科八年级下册第19章第一节
轻松回忆:
2:长方形和正方形的内角和是多少度?
1:三角形内角和是多少度?
(三角形内角和 180°)
(都是360°)
19.1 多边形内角和
沪科版本数学学科八年级下册第19章第一节
你能猜吗:
任意一个四边形的内角和是多少度?
请你任意画一个四边形,用量角器量一下各个内角的度数,计算一下四边形的内角和。
动动手:
(360°)
(360°)
19.1 多边形内角和
沪科版本数学学科八年级下册第19章第一节
动脑思考:
方法一:如图所示,利用辅助线将四边形分割成两个三角形
你能证明四边形的内角和等于360 °吗?
四边形的内角和
= 两个三角形的内角和相加
= 180 °+ 180 °
= 360 °
解题思路:把四边形问题转化为三角形问题来解决
19.1 多边形内角和
沪科版本数学学科八年级下册第19章第一节
在四边形内任找一点,作该点与四个顶点的连线,可将四边形分为4个三角形.由图知,四边形的内角和为:
方法二:
1
2
3
4
四边形的内角和
= 四个三角形的内角和-一个周角
= 180 °×4-360°
= 360 °
19.1 多边形内角和
沪科版本数学学科八年级下册第19章第一节
在四边形一边上找一点,作该点与另两个顶点的连线,可将四边形分为3个三角形.由图知,四边形的内角和为:
180°×3- 180° =360°
方法三:
1
2
3
19.1 多边形内角和
沪科版本数学学科八年级下册第19章第一节
180°×3- 180° =360°
在四边形外部找一点,作该点与另四个顶点的连线.由图知,四边形的内角和为:
方法四:
1
2
19.1 多边形内角和
沪科版本数学学科八年级下册第19章第一节
请选择一种你喜欢的方法,试说明五边形、六边形的内角和
19.1 多边形内角和
沪科版本数学学科八年级下册第19章第一节
n边形的边数 3 4 5 6 7 … n
分成三角形的个数 …
多边形的内角和 …
1
180°
2
3
4
5
360°
540°
720°
900°
n-2
(n-2)×180°
探索多(n)边形的内角和
19.1 多边形内角和
沪科版本数学学科八年级下册第19章第一节
n边形的内角和等于 (n-2)×180°
由此等式我们可以知道:
已知多边形的边数可以求出它的内角和,反之,已知多边形的内角和也可以求出它的边数
19.1 多边形内角和
沪科版本数学学科八年级下册第19章第一节
学以致用
2、十边形的内角和是( );如果十边形的各个内角都相等,那么它的一个内角是( )
1、七边形内角和为( )
900°
1440 °
144°
分析:(n-2)×180°=(7-2)×180°=900°
分析:(n-2)×180°=(10-2)×180°=1440°
1440°÷10=144°
19.1 多边形内角和
沪科版本数学学科八年级下册第19章第一节
学以致用
3、多边形内角和为1080°则它是( )边形。
4、多边形内角和为1800°则它是( )边形。
八
十二
分析:设多边形的边数为n,由题意得:
(n-2)×180°=1080°
解这个方程得:n=8
分析:设多边形的边数为n,由题意得:
(n-2)×180°=1800°
解这个方程得:n=12
19.1 多边形内角和
沪科版本数学学科八年级下册第19章第一节
如果一个四边形的一组对角互补,那么另一组对角有什么关系?
解:如图,四边形ABCD中,∠A+∠C=180°。
∵∠A+∠B+∠C+∠D=(4-2)×360°=180
∴∠B+∠D= 360°-(∠A+∠C)=180°
这就是说:如果四边形一组对角互补,那么另一组对角也互补.
分析:如图,在四边形ABCD 中 ,要求∠B与∠D的关系,由于已知∠A+∠C=180°,所以可以从四边形的内角和入手,就可得到完满的答案.
加深理解
