9.1.2 不等式的性质 第二课时 课件(共33张PPT)
文档属性
| 名称 | 9.1.2 不等式的性质 第二课时 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 753.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-14 07:39:12 | ||
图片预览










文档简介
(共33张PPT)
9.1.2 不等式的性质
第2课时
不等式与不等式组
人教版-数学-七年级-下册
知识回顾
不等式的性质有哪些?
不等式两边加(或减)同一个数(或式子),不等号的方向不变.
不等式两边乘(或除以)同一个正数,不等号的方向不变.
不等式两边乘(或除以)同一个负数,不等号的方向改变.
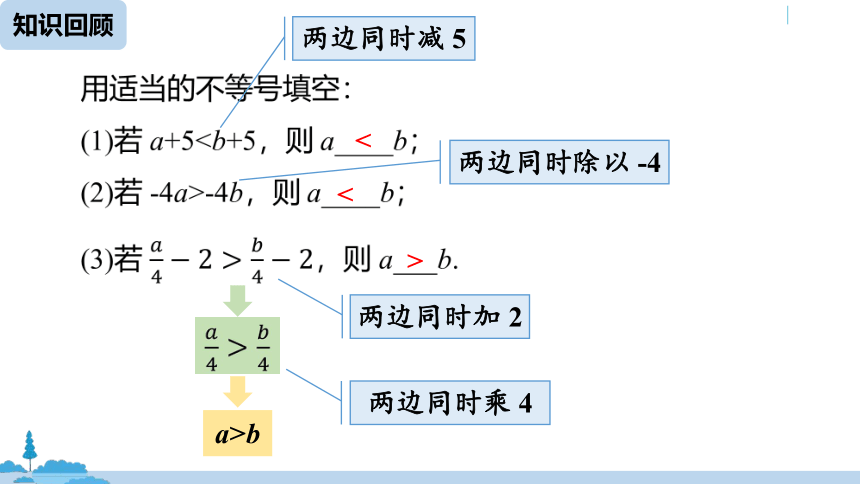
知识回顾
<
<
>
两边同时减 5
两边同时除以 -4
a>b
两边同时加 2
两边同时乘 4
学习目标
1.进一步了解不等式的基本性质,会用不等式的基本性质解简单的不等式.
2.学会并准确运用不等式表示数量关系,形成在表达中渗透数形结合的思想.
课堂导入
我们知道解方程需要依据等式的性质,同样解不等式也可以依据不等式的性质进行,本节课我们就来学习怎样利用不等式的基本性质解不等式.
新知探究
知识点:不等式的性质的应用
分析:解不等式,就是要借助不等式的性质使不等式逐步化为 x>a 或 x新知探究
解:(1)根据不等式的性质1,不等式两边加 7,不等号的方向不变,
所以 x-7+7>26+7,
即 x>33.
这个不等式的解集在数轴上的表示如图所示:
0
33
(1) x-7>26;
新知探究
0
1
(2) 3x<2x+1;
解:(2)根据不等式的性质1,不等式两边减 2x,不等号的方向不变,
所以 3x-2x<2x+1-2x,
即 x<1.
这个不等式的解集在数轴上的表示如图所示:
新知探究
0
75
新知探究
(4) -4x>3.
0
新知探究
利用不等式的性质1可简化为“移项”;利用不等式的性质2或性质3就是把未知数的系数化为1,要注意不等式两边乘(或除以)同一个负数时,不等号要改变方向.
新知探究
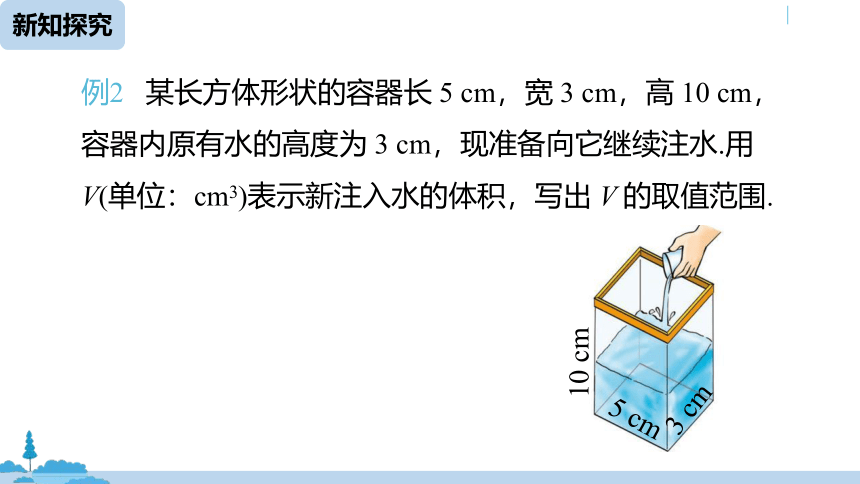
例2 某长方体形状的容器长 5 cm,宽 3 cm,高 10 cm,容器内原有水的高度为 3 cm,现准备向它继续注水.用V(单位:cm3)表示新注入水的体积,写出 V 的取值范围.
5 cm
3 cm
10 cm
新知探究
解:新注入水的体积 V 与原有水的体积的和不能超过容器的容积,即
V+3×5×3≤3×5×10,
V≤105.
又由于新注入水的体积不能是负数,
因此,V 的取值范围是 V ≥0 并且 V≤105.
在数轴上表示 V 的取值范围如图所示:
在表示 0 和 105 的点上画实心圆点,表示取值范围包含这两个数.
0
105
新知探究
①审:审清题意,弄懂已知什么,求什么,以及各个数量之间的关系.
②设:设未知数,一般是与所求问题有直接关系的量.
③找:找出题中所有的不等关系,特别是隐含的数量关系.
④列:列出不等式.
⑤解:分别解出每个不等式的解集,再求其公共部分,得出结果.
⑥答:根据所得结果作出回答.
列不等式处理实际问题的一般步骤:
跟踪训练
用不等式的性质解下列不等式,并在数轴上表示解集.
(1) x+5>-1;
解:(1)根据不等式的性质1,不等式两边减 5,不等号的方向不变,
所以 x+5-5>-1-5,
即 x>-6.
这个不等式的解集在数轴上的表示如图所示:
0
-6
用不等式的性质解下列不等式,并在数轴上表示解集.
(2) 4x<3x-5;
解:(2)根据不等式的性质1,不等式两边减 3x,不等号的方向不变,
所以 4x-3x<3x-5-3x ,
即 x<-5.
这个不等式的解集在数轴上的表示如图所示:
0
-5
跟踪训练
0
6
跟踪训练
用不等式的性质解下列不等式,并在数轴上表示解集.
(4) -8x>10.
0
跟踪训练
随堂练习
1.不等式 1-x≥2 的解集在数轴上表示正确的是( )
x≤-1
-2
-1
0
-2
-1
0
-2
-1
0
-2
-1
0
A
A
B
C
D
2.利用不等式的性质解下列不等式,并在数轴上表示解集.
(1) x+3<-2;
随堂练习
解:(1)根据不等式的性质1,不等式两边减 3,不等号的方向不变,
所以 x+3-3<-2-3,
即 x<-5.
这个不等式的解集在数轴上的表示如图所示:
0
-5
2.利用不等式的性质解下列不等式,并在数轴上表示解集.
(2) 9x>8x+1;
随堂练习
解:(2)根据不等式的性质1,不等式两边减 8x,不等号的方向不变,
所以 9x-8x>8x+1-8x ,
即 x>1.
这个不等式的解集在数轴上的表示如图所示:
0
1
随堂练习
0
-8
2.利用不等式的性质解下列不等式,并在数轴上表示解集.
(4) -10x ≤ 5.
随堂练习
0
随堂练习
3.已知在某超市内购物总金额超过 190 元时,购物总金额有打 8 折的优惠.安妮带了 200 元到该超市买棒棒糖,若棒棒糖每根 9 元,则她最多可买多少根棒棒糖?
课堂小结
列不等式处理实际问题的一般步骤:
审
设
找
列
解
答
拓展提升
1.不等式 5x+1≥3x-1 的解集在数轴上表示正确的是( )
-2
-1
0
1
A
B
C
D
-2
-1
0
1
-2
-1
0
1
-2
-1
0
1
2x+1≥-1
2x≥-2
两边同时减 3x
两边同时减1
x≥-1
两边同时除以2
B
2
0
拓展提升
解:(2)根据不等式的性质1,不等式两边减 7x,不等号的方向不变,
所以 5x-6-7x≤7x-4-7x,即 -2x-6≤-4.
根据不等式的性质1,不等式两边加 6,不等号的方向不变,
所以 -2x-6+6≤-4+6,即 -2x≤2.
拓展提升
0
-1
拓展提升
拓展提升
3.“春种一粒粟,秋收万颗子”,唐代诗人李绅这句诗中的“粟”即谷子(去皮后则称为“小米”),被誉为中华民族的哺育作物.
2020年,某省谷子种植面积已达 324 万亩,平均亩产量约为 320 kg.2021年,若该省谷子的平均亩产量仍保持 320 kg 不变,则要
使谷子的年总产量不低于 108 万吨,该省至少应再多种植多少万
亩的谷子?
列不等式时注意不等号两边的单位要统一.本题易因忽略320 kg的单位而直接列不等式320x≥108致错.
拓展提升
还有其他解法吗?
拓展提升
直接设未知数列不等式:
课后作业
请完成课本后习题第5、7、8题.
9.1.2 不等式的性质
第2课时
不等式与不等式组
人教版-数学-七年级-下册
知识回顾
不等式的性质有哪些?
不等式两边加(或减)同一个数(或式子),不等号的方向不变.
不等式两边乘(或除以)同一个正数,不等号的方向不变.
不等式两边乘(或除以)同一个负数,不等号的方向改变.
知识回顾
<
<
>
两边同时减 5
两边同时除以 -4
a>b
两边同时加 2
两边同时乘 4
学习目标
1.进一步了解不等式的基本性质,会用不等式的基本性质解简单的不等式.
2.学会并准确运用不等式表示数量关系,形成在表达中渗透数形结合的思想.
课堂导入
我们知道解方程需要依据等式的性质,同样解不等式也可以依据不等式的性质进行,本节课我们就来学习怎样利用不等式的基本性质解不等式.
新知探究
知识点:不等式的性质的应用
分析:解不等式,就是要借助不等式的性质使不等式逐步化为 x>a 或 x新知探究
解:(1)根据不等式的性质1,不等式两边加 7,不等号的方向不变,
所以 x-7+7>26+7,
即 x>33.
这个不等式的解集在数轴上的表示如图所示:
0
33
(1) x-7>26;
新知探究
0
1
(2) 3x<2x+1;
解:(2)根据不等式的性质1,不等式两边减 2x,不等号的方向不变,
所以 3x-2x<2x+1-2x,
即 x<1.
这个不等式的解集在数轴上的表示如图所示:
新知探究
0
75
新知探究
(4) -4x>3.
0
新知探究
利用不等式的性质1可简化为“移项”;利用不等式的性质2或性质3就是把未知数的系数化为1,要注意不等式两边乘(或除以)同一个负数时,不等号要改变方向.
新知探究
例2 某长方体形状的容器长 5 cm,宽 3 cm,高 10 cm,容器内原有水的高度为 3 cm,现准备向它继续注水.用V(单位:cm3)表示新注入水的体积,写出 V 的取值范围.
5 cm
3 cm
10 cm
新知探究
解:新注入水的体积 V 与原有水的体积的和不能超过容器的容积,即
V+3×5×3≤3×5×10,
V≤105.
又由于新注入水的体积不能是负数,
因此,V 的取值范围是 V ≥0 并且 V≤105.
在数轴上表示 V 的取值范围如图所示:
在表示 0 和 105 的点上画实心圆点,表示取值范围包含这两个数.
0
105
新知探究
①审:审清题意,弄懂已知什么,求什么,以及各个数量之间的关系.
②设:设未知数,一般是与所求问题有直接关系的量.
③找:找出题中所有的不等关系,特别是隐含的数量关系.
④列:列出不等式.
⑤解:分别解出每个不等式的解集,再求其公共部分,得出结果.
⑥答:根据所得结果作出回答.
列不等式处理实际问题的一般步骤:
跟踪训练
用不等式的性质解下列不等式,并在数轴上表示解集.
(1) x+5>-1;
解:(1)根据不等式的性质1,不等式两边减 5,不等号的方向不变,
所以 x+5-5>-1-5,
即 x>-6.
这个不等式的解集在数轴上的表示如图所示:
0
-6
用不等式的性质解下列不等式,并在数轴上表示解集.
(2) 4x<3x-5;
解:(2)根据不等式的性质1,不等式两边减 3x,不等号的方向不变,
所以 4x-3x<3x-5-3x ,
即 x<-5.
这个不等式的解集在数轴上的表示如图所示:
0
-5
跟踪训练
0
6
跟踪训练
用不等式的性质解下列不等式,并在数轴上表示解集.
(4) -8x>10.
0
跟踪训练
随堂练习
1.不等式 1-x≥2 的解集在数轴上表示正确的是( )
x≤-1
-2
-1
0
-2
-1
0
-2
-1
0
-2
-1
0
A
A
B
C
D
2.利用不等式的性质解下列不等式,并在数轴上表示解集.
(1) x+3<-2;
随堂练习
解:(1)根据不等式的性质1,不等式两边减 3,不等号的方向不变,
所以 x+3-3<-2-3,
即 x<-5.
这个不等式的解集在数轴上的表示如图所示:
0
-5
2.利用不等式的性质解下列不等式,并在数轴上表示解集.
(2) 9x>8x+1;
随堂练习
解:(2)根据不等式的性质1,不等式两边减 8x,不等号的方向不变,
所以 9x-8x>8x+1-8x ,
即 x>1.
这个不等式的解集在数轴上的表示如图所示:
0
1
随堂练习
0
-8
2.利用不等式的性质解下列不等式,并在数轴上表示解集.
(4) -10x ≤ 5.
随堂练习
0
随堂练习
3.已知在某超市内购物总金额超过 190 元时,购物总金额有打 8 折的优惠.安妮带了 200 元到该超市买棒棒糖,若棒棒糖每根 9 元,则她最多可买多少根棒棒糖?
课堂小结
列不等式处理实际问题的一般步骤:
审
设
找
列
解
答
拓展提升
1.不等式 5x+1≥3x-1 的解集在数轴上表示正确的是( )
-2
-1
0
1
A
B
C
D
-2
-1
0
1
-2
-1
0
1
-2
-1
0
1
2x+1≥-1
2x≥-2
两边同时减 3x
两边同时减1
x≥-1
两边同时除以2
B
2
0
拓展提升
解:(2)根据不等式的性质1,不等式两边减 7x,不等号的方向不变,
所以 5x-6-7x≤7x-4-7x,即 -2x-6≤-4.
根据不等式的性质1,不等式两边加 6,不等号的方向不变,
所以 -2x-6+6≤-4+6,即 -2x≤2.
拓展提升
0
-1
拓展提升
拓展提升
3.“春种一粒粟,秋收万颗子”,唐代诗人李绅这句诗中的“粟”即谷子(去皮后则称为“小米”),被誉为中华民族的哺育作物.
2020年,某省谷子种植面积已达 324 万亩,平均亩产量约为 320 kg.2021年,若该省谷子的平均亩产量仍保持 320 kg 不变,则要
使谷子的年总产量不低于 108 万吨,该省至少应再多种植多少万
亩的谷子?
列不等式时注意不等号两边的单位要统一.本题易因忽略320 kg的单位而直接列不等式320x≥108致错.
拓展提升
还有其他解法吗?
拓展提升
直接设未知数列不等式:
课后作业
请完成课本后习题第5、7、8题.
