直线的倾斜角和斜率
图片预览








文档简介
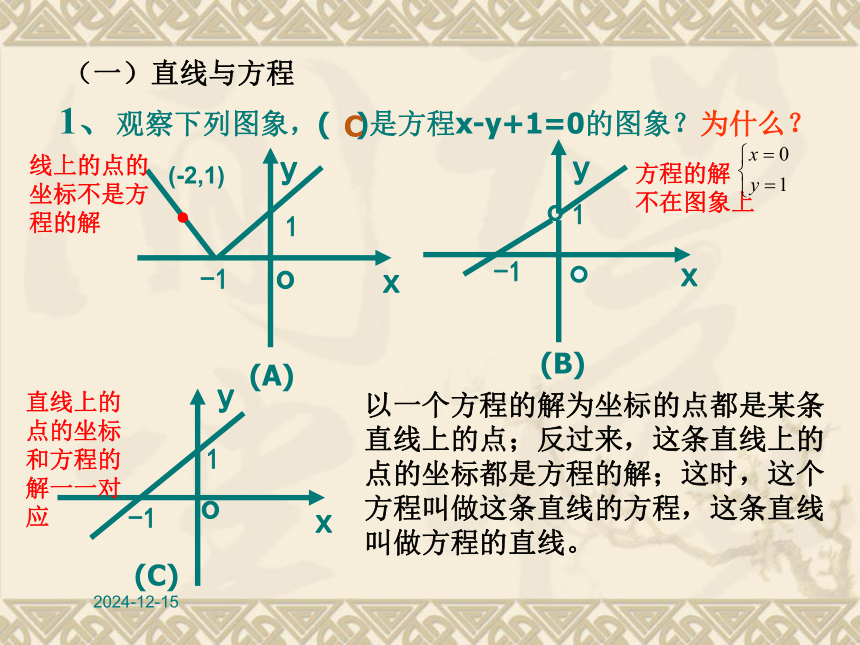
课件33张PPT。2019/1/18直线的倾斜角和斜率2019/1/18在初中,我们学过关系式y=x+2,它表示什么?一、复习练习x-y+2=0既可以表示二元一次方程,又可以表示一次函数改为x-y+2=0呢? 关系式y=x2 +2呢?y=x2 +2既可以表示二元二次方程,又可以表示二次函数2019/1/18? 1、观察下列图象,( )是方程x-y+1=0的图象?为什么?
y1xo-1(C)C线上的点的
坐标不是方
程的解1xy-1(B)o直线上的
点的坐标
和方程的
解一一对
应(-2,1)以一个方程的解为坐标的点都是某条
直线上的点;反过来,这条直线上的
点的坐标都是方程的解;这时,这个
方程叫做这条直线的方程,这条直线
叫做方程的直线。(一)直线与方程方程的解
不在图象上2019/1/18 以一个方程的解为坐标的点都是某条直线上的点;反过来,这条直线上的点的坐标都是方程的解;这时,这个方程叫做这条直线的方程,这条直线叫做方程的直线
总结:有了直线与方程这种对应关系,给一个方程的直线,我
们可以写出它的方程;给一个直线的方程,我们可以画出它的图象,
从而通过方程来研究直线的有关性质。(一)直线与方程 例如:方程y=2x+1所表示的直线,也可称为直线y=2x+1,此时
的方程和直线可以混为一谈。同时,我们也可以由方程y=2x+1有一
解 说明直线y=2x+1是一条过(0,1)点的直线。2019/1/181、探究1:连接正方形的对角线
活动1.如何用直尺连对角线,依据是什么?
活动2.如何用等腰直角三角板连对角线,依据是什么? 二、探究练习:2019/1/18说明:确定直线的两种方法:一种是两点可以确定一条直线,另一种是也可由一点和角(两条相交直线所成的角)来确定二、探究练习:1、探究1:连接正方形的对角线
活动1.如何用直尺连对角线,依据是什么?
活动2.如何用等腰直角三角板连对角线,依据是什么? 2019/1/182.深入研究,得出定义问1 .下图中的两条直线有什么异同? 问2. 以哪条直线做为参照直线来确定这个角比较好呢? 说明:用x轴定义这个角与三角函数相吻合,利于下一步用三角函
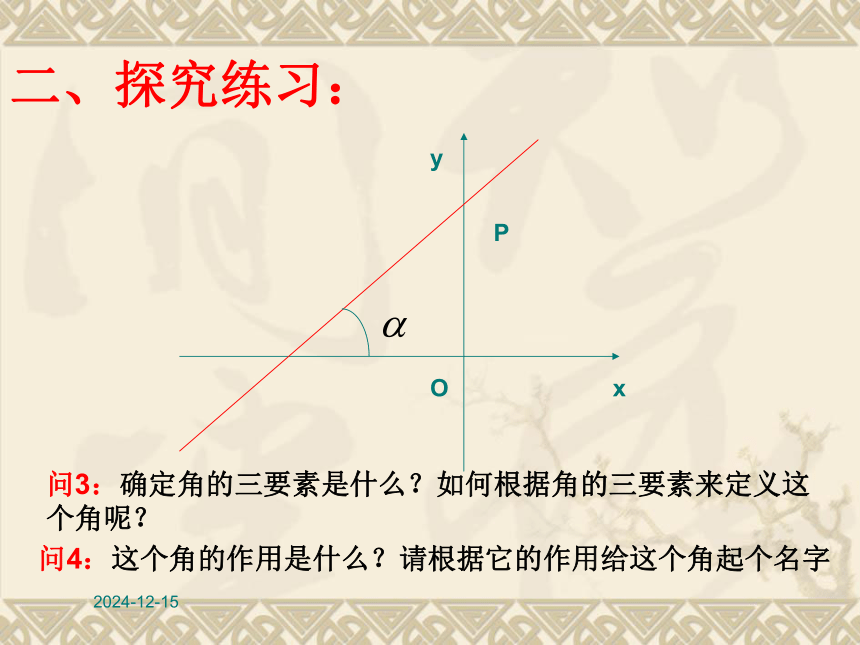
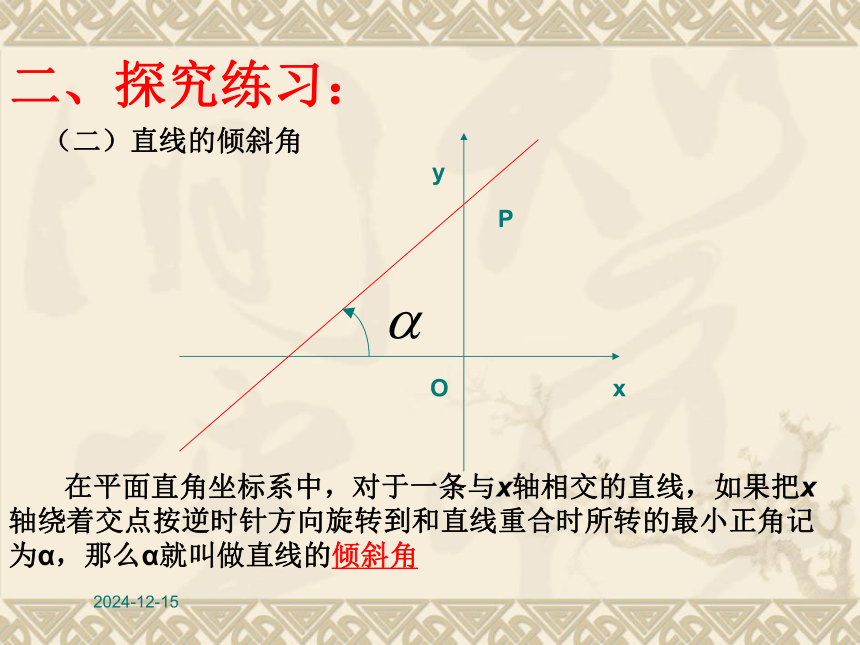
数值求这个角 二、探究练习:y2019/1/18OxyP二、探究练习:问3:确定角的三要素是什么?如何根据角的三要素来定义这个角呢?问4:这个角的作用是什么?请根据它的作用给这个角起个名字2019/1/18OxyP 在平面直角坐标系中,对于一条与x轴相交的直线,如果把x
轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记
为α,那么α就叫做直线的倾斜角 二、探究练习:(二)直线的倾斜角2019/1/18 在平面直角坐标系中,对于一条与x轴相交的直线,如果把x
轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记
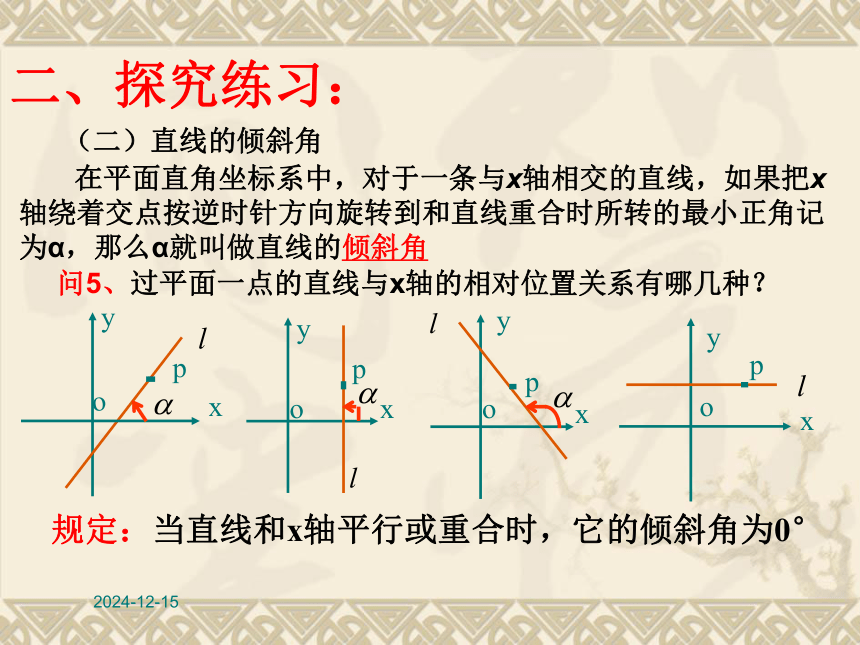
为α,那么α就叫做直线的倾斜角 二、探究练习:(二)直线的倾斜角2019/1/18规定:当直线和x轴平行或重合时,它的倾斜角为0°二、探究练习: 在平面直角坐标系中,对于一条与x轴相交的直线,如果把x
轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记
为α,那么α就叫做直线的倾斜角问5、过平面一点的直线与x轴的相对位置关系有哪几种?(二)直线的倾斜角2019/1/18 (2)倾斜角的范围:0°≤α<180°或0≤α<π 特别地,当 与 轴平行或重合时,规定倾斜角为0° 说明:(1)这个定义包括两个部分,从形的方面刻画直线对x轴的倾斜程度。(3)这个定义三个要点:
①直线和x轴的交点;
②直线按逆时针方向旋转;
③最小正角二、探究练习: 在平面直角坐标系中,对于一条与x轴相交的直线,如果把x
轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记
为α,那么α就叫做直线的倾斜角(二)直线的倾斜角2019/1/18 随堂练习:下列图中标出的直线的倾斜角对不对?如果不对,违背了定义中的哪一条?
xyoxyoxyoxy(1)(2)(3)(4)二、探究练习:(二)直线的倾斜角2019/1/18 (2)倾斜角的范围:0°≤α<180°或0≤α<π 特别地,当 与 轴平行或重合时,规定倾斜角为0°说明:(1)这个定义包括两个部分,从形的方面刻画直线对x 轴的倾斜程度。(3)这个定义三个要点:
①直线和x轴的交点;
②直线按逆时针方向旋转;
③最小正角(4)直线与倾斜角的对应关系: 二、探究练习: 在平面直角坐标系中,对于一条与x轴相交的直线,如果把x
轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记
为α,那么α就叫做直线的倾斜角(二)直线的倾斜角2019/1/182019/1/18 (2)倾斜角的范围:0°≤α<180°或0≤α<π 特别地,当 与 轴平行或重合时,规定倾斜角为0°说明:(1)这个定义包括两个部分,从形的方面刻画直线对x 轴的倾斜程度。(3)这个定义三个要点:
①直线和x轴的交点;
②直线按逆时针方向旋转;
③最小正角(4)直线与倾斜角的对应关系: 二、探究练习: 在平面直角坐标系中,对于一条与x轴相交的直线,如果把x
轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记
为α,那么α就叫做直线的倾斜角(二)直线的倾斜角每一条直线都有
唯一的倾斜角2019/1/18 在平面直角坐标系中,对于一条与x轴相交的直线,如果把x
轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记
为α,那么α就叫做直线的倾斜角 问6:如何度量 ?
直线方程能否体现直线的倾斜角?y=kx+b(二)直线的倾斜角二、探究练习:2019/1/18 3、观察下列图形和方程,你有什么发现?二、探究练习:(二)直线的倾斜角直线的倾斜程度也跟方程中x的系数有关2019/1/18二、探究练习: 4、探究2:按要求完成下表:1-1(二)直线的倾斜角2019/1/18二、探究练习: xOy(二)直线的倾斜角2019/1/18 二、探究练习:(二)直线的倾斜角xOy6002019/1/18二、探究练习: 5、探究2:写出下列直线的倾斜角,并填写下表1-1(二)直线的倾斜角猜想:方程中
X的系数等于
倾斜角的正切
值。
数学试验2019/1/18二、探究练习:我们把倾斜角的正切叫做斜率问7:是不是所有的倾斜角的正切都存在?(二)直线的倾斜角2019/1/18定义:倾斜角不是90°的直线,它的倾斜角的正切叫做这条直线的斜率.记作k,即说明:(1)斜率是一个数,从数的方面刻画直线对x轴的倾斜程度 .
二、探究练习:(三)直线的斜率(2)直线存在倾斜角,是直线存在斜率的必要不充分条件2019/1/18定义:倾斜角不是90°的直线,它的倾斜角的正切叫做这条直线的斜率.记作k,即说明:(1)斜率是一个数,从数的方面刻画直线对x轴的倾斜程度 .
二、探究练习:(三)直线的斜率(2)直线存在倾斜角,是直线存在斜率的必要不充分条件回顾获得定义的过程后思考:2019/1/18定义:倾斜角不是90°的直线,它的倾斜角的正切叫做这条直线的斜率.记作k,即说明:(1)斜率是一个数,从数的方面刻画直线对x轴的倾斜程度 .
二、探究练习:(三)直线的斜率(2)直线存在倾斜角,是直线存在斜率的必要不充分条件(3)直线的斜率使直线方程体现出了直线的外部特征
比如:直线方程y=2x+1中x的系数2就是直线的斜率2019/1/18 二、探究练习:例1:如图,直线L1的倾斜角 =300,直线l2⊥l1,求l1,l2 的斜率。(四)例题选讲2019/1/18 二、探究练习:例1:如图,直线L1的倾斜角 =300,直线l2⊥l1,求l1,l2 的斜率。例2:已知斜率k求直线的倾斜角
(1)k=1 (2)k=(四)例题选讲2019/1/18 二、探究练习:例1:如图,直线L1的倾斜角 =300,直线l2⊥l1,求l1,l2 的斜率。例2:已知斜率k求直线的倾斜角
(1)k=1 (2)k=(四)例题选讲例3:指出下列直线的倾斜角和斜率:
2019/1/18 三、巩固练习:1、关于直线的倾斜角和斜率,下列哪些说法是正确的( )
A.任一条直线都有倾斜角,也都有斜率;
B.直线的倾斜角越大,它的斜率就越大;
C.平行于x轴的直线的倾斜角是0或π;
D.两直线的斜率相等,它们的倾斜角相等
E.两直线的倾斜角相等,它们的斜率相等.
F.直线斜率的范围是(-∞,+∞).2.若直线L的方程为2x—y+3=0,则在直线L上的点的坐标是(? )
?? A(1,-1)? B(-1,1) C(2,1) D(1,2)3.求倾斜分别为 的直线的斜率。4.直线L1的斜率为3,直线L2的倾斜角是直线L1的2倍,求直线L2的斜率。2019/1/18四、归纳练习:直线的倾斜角和斜率从形的方面(图象)从数的方面(方程)每条直线都有唯一的倾斜角倾斜角为90o直线无斜率0°≤α<180° (-∞,+∞)倾斜角存在斜率不一
定存在,取正切值 有斜率则一定有倾
斜角,反正切运算 2019/1/18 五、课外作业:?1、教材? 37页?? 1,2题2、研究性学习:求出直线的斜率2019/1/18谢谢!再见!
y1xo-1(C)C线上的点的
坐标不是方
程的解1xy-1(B)o直线上的
点的坐标
和方程的
解一一对
应(-2,1)以一个方程的解为坐标的点都是某条
直线上的点;反过来,这条直线上的
点的坐标都是方程的解;这时,这个
方程叫做这条直线的方程,这条直线
叫做方程的直线。(一)直线与方程方程的解
不在图象上2019/1/18 以一个方程的解为坐标的点都是某条直线上的点;反过来,这条直线上的点的坐标都是方程的解;这时,这个方程叫做这条直线的方程,这条直线叫做方程的直线
总结:有了直线与方程这种对应关系,给一个方程的直线,我
们可以写出它的方程;给一个直线的方程,我们可以画出它的图象,
从而通过方程来研究直线的有关性质。(一)直线与方程 例如:方程y=2x+1所表示的直线,也可称为直线y=2x+1,此时
的方程和直线可以混为一谈。同时,我们也可以由方程y=2x+1有一
解 说明直线y=2x+1是一条过(0,1)点的直线。2019/1/181、探究1:连接正方形的对角线
活动1.如何用直尺连对角线,依据是什么?
活动2.如何用等腰直角三角板连对角线,依据是什么? 二、探究练习:2019/1/18说明:确定直线的两种方法:一种是两点可以确定一条直线,另一种是也可由一点和角(两条相交直线所成的角)来确定二、探究练习:1、探究1:连接正方形的对角线
活动1.如何用直尺连对角线,依据是什么?
活动2.如何用等腰直角三角板连对角线,依据是什么? 2019/1/182.深入研究,得出定义问1 .下图中的两条直线有什么异同? 问2. 以哪条直线做为参照直线来确定这个角比较好呢? 说明:用x轴定义这个角与三角函数相吻合,利于下一步用三角函
数值求这个角 二、探究练习:y2019/1/18OxyP二、探究练习:问3:确定角的三要素是什么?如何根据角的三要素来定义这个角呢?问4:这个角的作用是什么?请根据它的作用给这个角起个名字2019/1/18OxyP 在平面直角坐标系中,对于一条与x轴相交的直线,如果把x
轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记
为α,那么α就叫做直线的倾斜角 二、探究练习:(二)直线的倾斜角2019/1/18 在平面直角坐标系中,对于一条与x轴相交的直线,如果把x
轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记
为α,那么α就叫做直线的倾斜角 二、探究练习:(二)直线的倾斜角2019/1/18规定:当直线和x轴平行或重合时,它的倾斜角为0°二、探究练习: 在平面直角坐标系中,对于一条与x轴相交的直线,如果把x
轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记
为α,那么α就叫做直线的倾斜角问5、过平面一点的直线与x轴的相对位置关系有哪几种?(二)直线的倾斜角2019/1/18 (2)倾斜角的范围:0°≤α<180°或0≤α<π 特别地,当 与 轴平行或重合时,规定倾斜角为0° 说明:(1)这个定义包括两个部分,从形的方面刻画直线对x轴的倾斜程度。(3)这个定义三个要点:
①直线和x轴的交点;
②直线按逆时针方向旋转;
③最小正角二、探究练习: 在平面直角坐标系中,对于一条与x轴相交的直线,如果把x
轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记
为α,那么α就叫做直线的倾斜角(二)直线的倾斜角2019/1/18 随堂练习:下列图中标出的直线的倾斜角对不对?如果不对,违背了定义中的哪一条?
xyoxyoxyoxy(1)(2)(3)(4)二、探究练习:(二)直线的倾斜角2019/1/18 (2)倾斜角的范围:0°≤α<180°或0≤α<π 特别地,当 与 轴平行或重合时,规定倾斜角为0°说明:(1)这个定义包括两个部分,从形的方面刻画直线对x 轴的倾斜程度。(3)这个定义三个要点:
①直线和x轴的交点;
②直线按逆时针方向旋转;
③最小正角(4)直线与倾斜角的对应关系: 二、探究练习: 在平面直角坐标系中,对于一条与x轴相交的直线,如果把x
轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记
为α,那么α就叫做直线的倾斜角(二)直线的倾斜角2019/1/182019/1/18 (2)倾斜角的范围:0°≤α<180°或0≤α<π 特别地,当 与 轴平行或重合时,规定倾斜角为0°说明:(1)这个定义包括两个部分,从形的方面刻画直线对x 轴的倾斜程度。(3)这个定义三个要点:
①直线和x轴的交点;
②直线按逆时针方向旋转;
③最小正角(4)直线与倾斜角的对应关系: 二、探究练习: 在平面直角坐标系中,对于一条与x轴相交的直线,如果把x
轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记
为α,那么α就叫做直线的倾斜角(二)直线的倾斜角每一条直线都有
唯一的倾斜角2019/1/18 在平面直角坐标系中,对于一条与x轴相交的直线,如果把x
轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记
为α,那么α就叫做直线的倾斜角 问6:如何度量 ?
直线方程能否体现直线的倾斜角?y=kx+b(二)直线的倾斜角二、探究练习:2019/1/18 3、观察下列图形和方程,你有什么发现?二、探究练习:(二)直线的倾斜角直线的倾斜程度也跟方程中x的系数有关2019/1/18二、探究练习: 4、探究2:按要求完成下表:1-1(二)直线的倾斜角2019/1/18二、探究练习: xOy(二)直线的倾斜角2019/1/18 二、探究练习:(二)直线的倾斜角xOy6002019/1/18二、探究练习: 5、探究2:写出下列直线的倾斜角,并填写下表1-1(二)直线的倾斜角猜想:方程中
X的系数等于
倾斜角的正切
值。
数学试验2019/1/18二、探究练习:我们把倾斜角的正切叫做斜率问7:是不是所有的倾斜角的正切都存在?(二)直线的倾斜角2019/1/18定义:倾斜角不是90°的直线,它的倾斜角的正切叫做这条直线的斜率.记作k,即说明:(1)斜率是一个数,从数的方面刻画直线对x轴的倾斜程度 .
二、探究练习:(三)直线的斜率(2)直线存在倾斜角,是直线存在斜率的必要不充分条件2019/1/18定义:倾斜角不是90°的直线,它的倾斜角的正切叫做这条直线的斜率.记作k,即说明:(1)斜率是一个数,从数的方面刻画直线对x轴的倾斜程度 .
二、探究练习:(三)直线的斜率(2)直线存在倾斜角,是直线存在斜率的必要不充分条件回顾获得定义的过程后思考:2019/1/18定义:倾斜角不是90°的直线,它的倾斜角的正切叫做这条直线的斜率.记作k,即说明:(1)斜率是一个数,从数的方面刻画直线对x轴的倾斜程度 .
二、探究练习:(三)直线的斜率(2)直线存在倾斜角,是直线存在斜率的必要不充分条件(3)直线的斜率使直线方程体现出了直线的外部特征
比如:直线方程y=2x+1中x的系数2就是直线的斜率2019/1/18 二、探究练习:例1:如图,直线L1的倾斜角 =300,直线l2⊥l1,求l1,l2 的斜率。(四)例题选讲2019/1/18 二、探究练习:例1:如图,直线L1的倾斜角 =300,直线l2⊥l1,求l1,l2 的斜率。例2:已知斜率k求直线的倾斜角
(1)k=1 (2)k=(四)例题选讲2019/1/18 二、探究练习:例1:如图,直线L1的倾斜角 =300,直线l2⊥l1,求l1,l2 的斜率。例2:已知斜率k求直线的倾斜角
(1)k=1 (2)k=(四)例题选讲例3:指出下列直线的倾斜角和斜率:
2019/1/18 三、巩固练习:1、关于直线的倾斜角和斜率,下列哪些说法是正确的( )
A.任一条直线都有倾斜角,也都有斜率;
B.直线的倾斜角越大,它的斜率就越大;
C.平行于x轴的直线的倾斜角是0或π;
D.两直线的斜率相等,它们的倾斜角相等
E.两直线的倾斜角相等,它们的斜率相等.
F.直线斜率的范围是(-∞,+∞).2.若直线L的方程为2x—y+3=0,则在直线L上的点的坐标是(? )
?? A(1,-1)? B(-1,1) C(2,1) D(1,2)3.求倾斜分别为 的直线的斜率。4.直线L1的斜率为3,直线L2的倾斜角是直线L1的2倍,求直线L2的斜率。2019/1/18四、归纳练习:直线的倾斜角和斜率从形的方面(图象)从数的方面(方程)每条直线都有唯一的倾斜角倾斜角为90o直线无斜率0°≤α<180° (-∞,+∞)倾斜角存在斜率不一
定存在,取正切值 有斜率则一定有倾
斜角,反正切运算 2019/1/18 五、课外作业:?1、教材? 37页?? 1,2题2、研究性学习:求出直线的斜率2019/1/18谢谢!再见!
