人教新课标A版必修4第二章学案全集
文档属性
| 名称 | 人教新课标A版必修4第二章学案全集 |  | |
| 格式 | zip | ||
| 文件大小 | 28.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-17 22:13:03 | ||
图片预览




文档简介
高一新课程标准数学学案(必修4)
2.1平面向量的实际背景及基本概念
2.1.1-----2.1.3向量的有关概念及表示
学习目标:
1. 理解向量的有关概念及表示
2. 掌握向量的模,零向量,单位向量,平行向量,相等向量,共线向量的概念。
学习重点:
1. 向量,相等向量,共线向量的概念及向量的几何表示
2. 平行向量,相等向量和共线向量的区别和联系
学习过程:
一.学习引导
1. 在物理中什么叫矢量?什么叫标量?矢量标量各有哪些?
2. 在数学中----------。-------的量叫做向量,--------。---------的量称为数量。
3. 向量的表示:
(1) 几何表示:用--------表示向量
(2) 名称表示:用--------或--------表示向量
4. 向量的模:向量的------或--------。记作--------
5. 特殊向量
(1)------------------叫做零向量,方向---------
(2)------------------叫做单位向量,方向--------
同学们,请用几何表示两个单位向量
6. 向量间的关系
(1) 平行向量:方向----------的--------向量,规定:-----------向量与任一向量平行,记作-----------
(2) 相等向量:长度--------方向-------的向量,记作---------
(3) 共线向量:任一组----------向量都可以移动到--------------上,也叫----------向量
二.合作交流
平行向量,相等向量和共线向量的区别和联系?
三.随堂练习
1. 画出下列向量
(1)││=4 点A在点O正南方向
(2) ││=2 点B在点o南偏西30方向
2.,的长度相等吗 是相等向量吗
3.共线向量一定在同一直线上吗 1
四.能力提升
如图,设O 是正六边形ABCDEF的中点,分别写出图中与 OA,OB,OC 相等的向量(见课本)
反思小结
自我测评
1. 物理学中的作用力和反作用力是模____________且方向_________的共线向量。
2. 下列说法正确的是
A.若两个向量长度相等,则这两个向量为相等向量
B.零向量的方向任意旋转一个不是2 整数倍的角度后仍为零向量
C.平行向量的方向相同
D.所有的单位向量都相等
3. 判断下列命题是否正确
(1)若 ︱︱=︱︱则=
(2)两向量相等是他们的起点相同,终点相同
(3)若 AB= CD 则四边形ABCD 平行四边形
(4)若四边形ABCD 为平行四边形,则AB=CD
(5)若=, 则=
(6)若∥,∥则∥
高一新课程标准数学学案(必修4)
2.2.1 向量加法运算及其几何意义
学习目标:
1. 掌握向量的加法概念及运算法则。
2. 能利用向量的加法运算法则解决有关问题。
3.
学习重点:
作出两个向量的和向量
学习过程:
一.学习引导
1. 求---------------运算叫做向量的加法。
2. 向量加法的法则
(1) 三角形法则:--------------------------------------------
(2) 平行四边形法则----------------------------------------------------
规定+ = ____
3. 向量加法的运算律
(1) 交换律:----------------------------------------
(2) 结合律:-----------------------------------------
二.合作交流
a.b.处于什么位置时
(1)。︱=︱ +︱
(2)。︱=︱-︱(或︱-︱)
三.随堂练习
1.求作+
2.求和向量
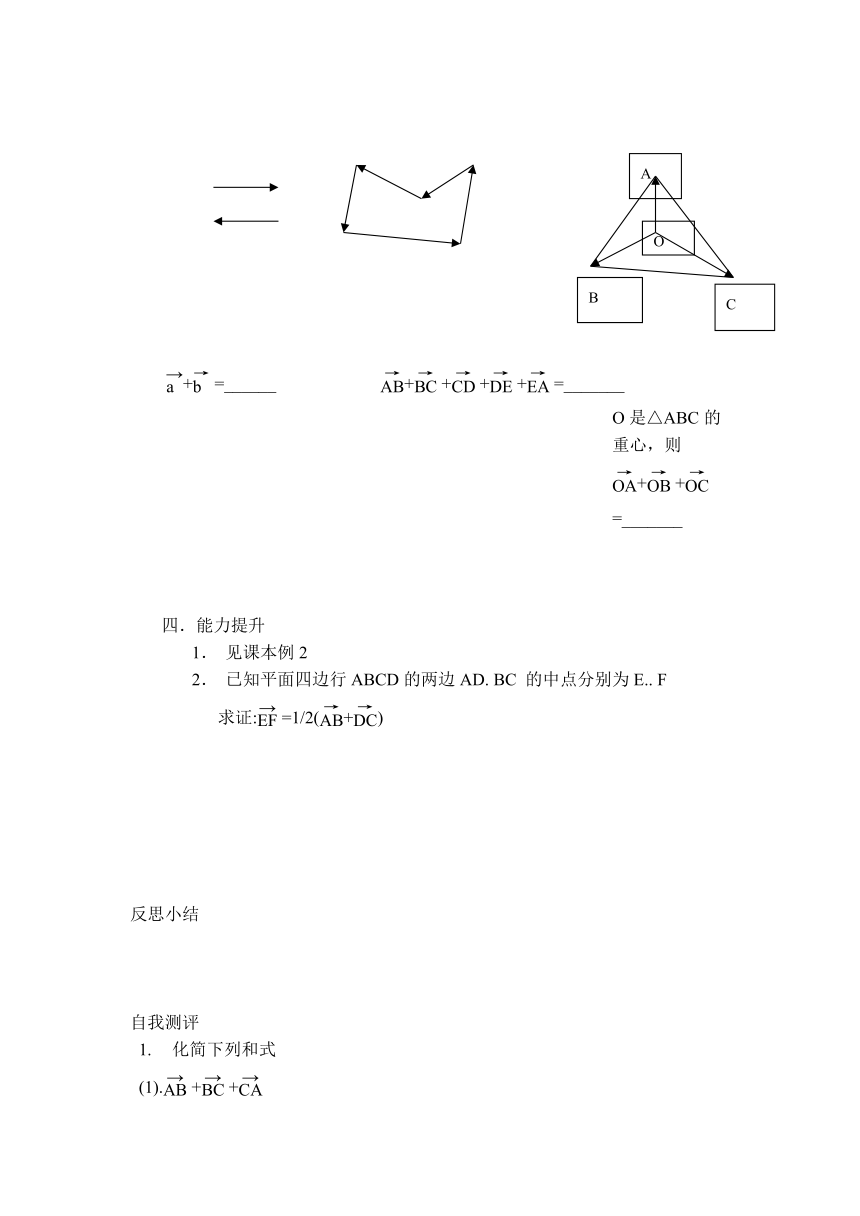
+ =______ + + + + =_______ O是△ABC的重心,则+ + =_______
四.能力提升
1. 见课本例2
2. 已知平面四边行ABCD的两边AD. BC 的中点分别为E.. F
求证: =1/2(+)
反思小结
自我测评
1. 化简下列和式
(1). + +
(2).( +)+ +
(3). + + +
2. 已知a. b.是非零向量.|a︱= |+︱需满足-------------,︱ +︱> +需满足-----------------------
3. 若O为△ABC内一点, + +则O是△ABC的------心.。
4. 设M为△ABC的重心,则下列各向量中与AB共线的是-----------
A. + + B。+ +
C. + + D。3C
高一新课程标准数学学案(必修4)
2.2.2 向量减法运算及其几何意义.
学习目标:
1. 掌握向量减法的概念及运算法则。
2. 能利用向量减法的运算法则解决有关问题。
学习重点;
作两个向量的差向量
学习过程:
一.学习引导
1. 相反向量:长度--------方向----------的向量。记作-----------
规定:零向量的相反向量是----------
2. 向量的减法:--------------------叫的差,记作--------
几何运算:三角形平移使两向量有相同的-------了,连接两个--------,方向指向-----------向量就是这两个向量的差。
二.合作交流
︱-︱< ︱<︱ +︱应满足什么条件
三.随堂练习
1. 求作–
2. 填空
- =___________, - =________,
四.能力提升
平行四边形ABCD, = ,表示,
反思小结
自我测评
1化简
① - + - ② - +
③ - - ④ + + -
2. 已知︱︱=8,︱︱=5,则︱︱的取值范围是____________________
3.作图验证 =-)
高一新课程标准数学学案(必修4)
2.2. 3向量数乘运算及其几何意义
学习目标:
1. 理解实数与向量的积的意义。
2. 理解两个向量共线的判断方法。
学习重点:
实数与向量的积的定义运算律几向量共线的条件。
学习过程:
一.学习引导
1. 向量的数乘:--------------与----------积是一个------------记作__________
(1)|︳=
(2)当Λ大于零时,Λ的方向与的方向_______
当Λ小于零时, Λ的方向与的方向_______
当Λ等于零时, Λ=_______
2. 数乘的运算律
(1)Λ(μ)=__________
(2)(Λ+μ)=__________
(3)Λ+)=___________
3. 向量共线:向)共线,当且仅当有唯一一个实数=
二.合作交流
1. 上面定理中为何强调
2. 与非共线的单位向量怎样表示?
三.能力提升
1.已知任意俩个非零向量,,试作 + +, =,你能判断三点之间的位置关系吗
2. 平行四边形ABCD的俩条对交线相交于点M,且=, =,用,表示, ,和
四.随堂练习
1. 化简
(1)5(-)+4(-)
(2)(x-y))-(x-y))
2 设1,2是两个不共线向量,已知=21+2,=1+32,若A,B,C三点共线,求R的值。
3. 已知1∥2 =1+2, =21-2,求证∥
反思小结
自我测评
1. 已知=1+22, =31-22,求+,3-2
在平行四边形ABCD中,M是AB的中点,N是BD上的一点,且BN=1/3BD,求证:M,N,C三点共线
3 =1/3, =1/3,求证: =1/3
4.P,Q分别为四边形ABCD的对角线AC,BD的中点, , =,用,表示
高一新课程标准数学学案(必修4)
2.3. 1平面向量基本定理
学习目标:
掌握平面向量的基本定理并应用之解题。
学习重点:
平面向量基本定理的应用。
学习过程:
一.学习引导
1. 已知不共线向量1,2,任意通过作图用1,2表示
2.平面向量的基本定理
如果1,2是同一平面内的两个向量,那么对于这一平面内的任意向量a ,_____________实数Λ1.Λ2,使a =_________
3.向量的夹角
已知两个非零向量和,作=, =,则θ=________叫做与的夹角
当θ=00时,a 与b __________
当θ=1800时,a 与b ___________
当θ=900时,a 与b _______________
二.合作交流
a =Λ11+Λ22,且a =m1+n2则Λ1,Λ2,m,n之间有何关系
三.随堂练习
1.在下列图中标出两向量的夹角
2.已知1,2求平面向量-21+32
四.能力提升
如图,O不共线, =t,用,表示
反思小结:
自我测评:
已知1,2不共线,若k1+2与1+k2共线,则实数k=_________
2.△ABC中,点M是BC的中点,点N在边AC上,且AN=2NC,AM与BN相交于点P,求AP:PM的值
设= =3, = =4,且与不共线,与相交于点E,试用和表示
高一新课程标准数学学案(必修4)
2.3.2平面向量的坐标表示及运算
学习目标
掌握平面向量的坐标表示及运算
学习重点:
理解平面向量的坐标表示及运算
学习过程:
一.学习引导
1.设么叫向量正交分解,
2向量怎样用坐标表示
3向量坐标运算
=(x1,y1) =(x2,y2)
=____________
= _____________
=________________
4已知A(x1,y1),B(x2,y2)则=____________︳︳_︳=———————
三.随堂练习
1. 已=(2,1) =(-3,4), +
2已知=(6,1), =(x,y), =(-2,-3)则=_________
3. 已知O(0,0),A(1,2),B(4,5), = +t,求t为何值时,点P在X轴上,
点P在Y轴上
四.能力提升
平行四边形ABCD的三个顶点A,B,C的坐标是(-2,1),(-1,3),(3,4)求顶点D的坐标
反思小结:
自我测评:
若三点A(1,1),B(2,-4),C(x,-9)共线,则x=____________
已知A(2,3),B(-4,5),则与共线的单位向量是_________________
点A(-1,2),a=(2,3),若=,则点B的坐标为_______________
=(k,12) =(-2,3),若- +共线则m/n=_______________
设=(k,12), =(4,5), =(10,k),则k为何值时A,B,C三点共线
=(3,-4), =(6,-3), =(5-m,-3-m),若A,B,C能构成三角形,求实数m应满足什么条件
C
O
A
B
2.1平面向量的实际背景及基本概念
2.1.1-----2.1.3向量的有关概念及表示
学习目标:
1. 理解向量的有关概念及表示
2. 掌握向量的模,零向量,单位向量,平行向量,相等向量,共线向量的概念。
学习重点:
1. 向量,相等向量,共线向量的概念及向量的几何表示
2. 平行向量,相等向量和共线向量的区别和联系
学习过程:
一.学习引导
1. 在物理中什么叫矢量?什么叫标量?矢量标量各有哪些?
2. 在数学中----------。-------的量叫做向量,--------。---------的量称为数量。
3. 向量的表示:
(1) 几何表示:用--------表示向量
(2) 名称表示:用--------或--------表示向量
4. 向量的模:向量的------或--------。记作--------
5. 特殊向量
(1)------------------叫做零向量,方向---------
(2)------------------叫做单位向量,方向--------
同学们,请用几何表示两个单位向量
6. 向量间的关系
(1) 平行向量:方向----------的--------向量,规定:-----------向量与任一向量平行,记作-----------
(2) 相等向量:长度--------方向-------的向量,记作---------
(3) 共线向量:任一组----------向量都可以移动到--------------上,也叫----------向量
二.合作交流
平行向量,相等向量和共线向量的区别和联系?
三.随堂练习
1. 画出下列向量
(1)││=4 点A在点O正南方向
(2) ││=2 点B在点o南偏西30方向
2.,的长度相等吗 是相等向量吗
3.共线向量一定在同一直线上吗 1
四.能力提升
如图,设O 是正六边形ABCDEF的中点,分别写出图中与 OA,OB,OC 相等的向量(见课本)
反思小结
自我测评
1. 物理学中的作用力和反作用力是模____________且方向_________的共线向量。
2. 下列说法正确的是
A.若两个向量长度相等,则这两个向量为相等向量
B.零向量的方向任意旋转一个不是2 整数倍的角度后仍为零向量
C.平行向量的方向相同
D.所有的单位向量都相等
3. 判断下列命题是否正确
(1)若 ︱︱=︱︱则=
(2)两向量相等是他们的起点相同,终点相同
(3)若 AB= CD 则四边形ABCD 平行四边形
(4)若四边形ABCD 为平行四边形,则AB=CD
(5)若=, 则=
(6)若∥,∥则∥
高一新课程标准数学学案(必修4)
2.2.1 向量加法运算及其几何意义
学习目标:
1. 掌握向量的加法概念及运算法则。
2. 能利用向量的加法运算法则解决有关问题。
3.
学习重点:
作出两个向量的和向量
学习过程:
一.学习引导
1. 求---------------运算叫做向量的加法。
2. 向量加法的法则
(1) 三角形法则:--------------------------------------------
(2) 平行四边形法则----------------------------------------------------
规定+ = ____
3. 向量加法的运算律
(1) 交换律:----------------------------------------
(2) 结合律:-----------------------------------------
二.合作交流
a.b.处于什么位置时
(1)。︱=︱ +︱
(2)。︱=︱-︱(或︱-︱)
三.随堂练习
1.求作+
2.求和向量
+ =______ + + + + =_______ O是△ABC的重心,则+ + =_______
四.能力提升
1. 见课本例2
2. 已知平面四边行ABCD的两边AD. BC 的中点分别为E.. F
求证: =1/2(+)
反思小结
自我测评
1. 化简下列和式
(1). + +
(2).( +)+ +
(3). + + +
2. 已知a. b.是非零向量.|a︱= |+︱需满足-------------,︱ +︱> +需满足-----------------------
3. 若O为△ABC内一点, + +则O是△ABC的------心.。
4. 设M为△ABC的重心,则下列各向量中与AB共线的是-----------
A. + + B。+ +
C. + + D。3C
高一新课程标准数学学案(必修4)
2.2.2 向量减法运算及其几何意义.
学习目标:
1. 掌握向量减法的概念及运算法则。
2. 能利用向量减法的运算法则解决有关问题。
学习重点;
作两个向量的差向量
学习过程:
一.学习引导
1. 相反向量:长度--------方向----------的向量。记作-----------
规定:零向量的相反向量是----------
2. 向量的减法:--------------------叫的差,记作--------
几何运算:三角形平移使两向量有相同的-------了,连接两个--------,方向指向-----------向量就是这两个向量的差。
二.合作交流
︱-︱< ︱<︱ +︱应满足什么条件
三.随堂练习
1. 求作–
2. 填空
- =___________, - =________,
四.能力提升
平行四边形ABCD, = ,表示,
反思小结
自我测评
1化简
① - + - ② - +
③ - - ④ + + -
2. 已知︱︱=8,︱︱=5,则︱︱的取值范围是____________________
3.作图验证 =-)
高一新课程标准数学学案(必修4)
2.2. 3向量数乘运算及其几何意义
学习目标:
1. 理解实数与向量的积的意义。
2. 理解两个向量共线的判断方法。
学习重点:
实数与向量的积的定义运算律几向量共线的条件。
学习过程:
一.学习引导
1. 向量的数乘:--------------与----------积是一个------------记作__________
(1)|︳=
(2)当Λ大于零时,Λ的方向与的方向_______
当Λ小于零时, Λ的方向与的方向_______
当Λ等于零时, Λ=_______
2. 数乘的运算律
(1)Λ(μ)=__________
(2)(Λ+μ)=__________
(3)Λ+)=___________
3. 向量共线:向)共线,当且仅当有唯一一个实数=
二.合作交流
1. 上面定理中为何强调
2. 与非共线的单位向量怎样表示?
三.能力提升
1.已知任意俩个非零向量,,试作 + +, =,你能判断三点之间的位置关系吗
2. 平行四边形ABCD的俩条对交线相交于点M,且=, =,用,表示, ,和
四.随堂练习
1. 化简
(1)5(-)+4(-)
(2)(x-y))-(x-y))
2 设1,2是两个不共线向量,已知=21+2,=1+32,若A,B,C三点共线,求R的值。
3. 已知1∥2 =1+2, =21-2,求证∥
反思小结
自我测评
1. 已知=1+22, =31-22,求+,3-2
在平行四边形ABCD中,M是AB的中点,N是BD上的一点,且BN=1/3BD,求证:M,N,C三点共线
3 =1/3, =1/3,求证: =1/3
4.P,Q分别为四边形ABCD的对角线AC,BD的中点, , =,用,表示
高一新课程标准数学学案(必修4)
2.3. 1平面向量基本定理
学习目标:
掌握平面向量的基本定理并应用之解题。
学习重点:
平面向量基本定理的应用。
学习过程:
一.学习引导
1. 已知不共线向量1,2,任意通过作图用1,2表示
2.平面向量的基本定理
如果1,2是同一平面内的两个向量,那么对于这一平面内的任意向量a ,_____________实数Λ1.Λ2,使a =_________
3.向量的夹角
已知两个非零向量和,作=, =,则θ=________叫做与的夹角
当θ=00时,a 与b __________
当θ=1800时,a 与b ___________
当θ=900时,a 与b _______________
二.合作交流
a =Λ11+Λ22,且a =m1+n2则Λ1,Λ2,m,n之间有何关系
三.随堂练习
1.在下列图中标出两向量的夹角
2.已知1,2求平面向量-21+32
四.能力提升
如图,O不共线, =t,用,表示
反思小结:
自我测评:
已知1,2不共线,若k1+2与1+k2共线,则实数k=_________
2.△ABC中,点M是BC的中点,点N在边AC上,且AN=2NC,AM与BN相交于点P,求AP:PM的值
设= =3, = =4,且与不共线,与相交于点E,试用和表示
高一新课程标准数学学案(必修4)
2.3.2平面向量的坐标表示及运算
学习目标
掌握平面向量的坐标表示及运算
学习重点:
理解平面向量的坐标表示及运算
学习过程:
一.学习引导
1.设么叫向量正交分解,
2向量怎样用坐标表示
3向量坐标运算
=(x1,y1) =(x2,y2)
=____________
= _____________
=________________
4已知A(x1,y1),B(x2,y2)则=____________︳︳_︳=———————
三.随堂练习
1. 已=(2,1) =(-3,4), +
2已知=(6,1), =(x,y), =(-2,-3)则=_________
3. 已知O(0,0),A(1,2),B(4,5), = +t,求t为何值时,点P在X轴上,
点P在Y轴上
四.能力提升
平行四边形ABCD的三个顶点A,B,C的坐标是(-2,1),(-1,3),(3,4)求顶点D的坐标
反思小结:
自我测评:
若三点A(1,1),B(2,-4),C(x,-9)共线,则x=____________
已知A(2,3),B(-4,5),则与共线的单位向量是_________________
点A(-1,2),a=(2,3),若=,则点B的坐标为_______________
=(k,12) =(-2,3),若- +共线则m/n=_______________
设=(k,12), =(4,5), =(10,k),则k为何值时A,B,C三点共线
=(3,-4), =(6,-3), =(5-m,-3-m),若A,B,C能构成三角形,求实数m应满足什么条件
C
O
A
B
