人教版数学七年级下册2022年暑假作业:相交线(word版含解析)
文档属性
| 名称 | 人教版数学七年级下册2022年暑假作业:相交线(word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 168.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-14 19:12:44 | ||
图片预览




文档简介
人教版数学七年级下册2022年暑假作业:相交线
一、填空题
1.下列说法中正确的有( )
①一个角的余角一定比这个角大;②同角的余角相等;③若∠1+∠2+∠3=180°,则∠1,∠2,∠3互补;④对顶角相等.
A.1个 B.2个 C.3个 D.4个
2.下列图形中,∠1与∠2是对顶角的是( )
A. B.
C. D.
3.已知平面内三条直线 与 相交,若 ,则 的度数为( )
A. B. C. D.
4.BP是∠ABC的平分线,CP是∠ACB的邻补角的平分线,∠ABP=20°,∠ACP=50°,则∠P=( )
A.30° B.40° C.50° D.60°
5.在同一平面内,若∠AOB=90 ,∠BOC=40 ,则∠AOB的平分线与∠BOC 的平分线的夹角等于( )
A.65 B.25 C.65 或25 D.60 或20
6.下列命题中真命题是( )
A.同位角相等 B.垂线段最短
C.相等的角是对顶角 D.互补的角是邻补角
7.已知:如图,,,求证:∥.下面为嘉琪同学的证明过程:
证明:∵,( ① ),
∴.又∵,∴
∴∥( ② ).
其中①②为解题依据,则下列描述正确的是( )
A.①代表内错角相等
B.②代表同位角相等,两直线平行
C.①代表对顶角相等
D.②代表同旁内角相等,两直线平行
8.如图,已知△ABC中,∠A=45°,∠ABC=105°,在CB延长线上有一点D,过点D作DE⊥AC于点E,则∠D=( )
A.60° B.65° C.70° D.75°
9.如图,若直线a∥直线b,∠1=40°,则∠2的度数为( )
A.40° B.50° C.140° D.160°
10.平面上三条直线两两相交最多能构成对顶角的对数是( ).
A.7 B.6 C.5 D.4
11.直线AB、CD交于点O,若∠AOC为35°,则∠BOD的度数为( )
A.30° B.35° C.55° D.145°
12.如图AB、CD交于点O,OE⊥AB于O,则下列不正确的是( )
A.∠AOC与∠BOD是对顶角 B.∠BOD和∠DOE互为余角
C.∠AOC和∠DOE互为余角 D.∠AOE和∠BOC是对顶角
13.下列说法正确的是( )
A.有公共顶点的两个角是对顶角
B.相等的角是对顶角
C.有公共顶点且相等的角是对顶角
D.对顶角相等
14.如图,下列说法正确的是( )
A. 与 是同旁内角 B. 与 是对顶角
C. 与 是内错角 D. 与 是同位角
15.一块含有45°的直角三角板和直尺如图放置,若∠1=55°,则∠2的度数是( )
A.30° B.35° C.40° D.45°
二、填空题
16.如图所示,直线AB,CD相交于点O,已知∠AOC=70°,OE平分∠BOD,则∠EOD= .
17.如图,直线AB,CD相交于点O,EO⊥AB于点O,∠EOD=56°23′,则∠BOC的度数为 .
18.已知∠A=65°,则∠A的余角是
19.如图, , 平分 ,直尺与 垂直,则∠1等于 .
20.如图,直线AB、CD相交于点O,若∠AOD=28°,则∠BOC= ,∠AOC= .
三、解答题
21.说明理由
如图,∠1+∠2=230°,b∥c, 则∠1、∠2、∠3、∠4各是多少度?
解:∵ ∠1=∠2 ( )
∠1+∠2=230°
∴∠1 =∠2 =( ) (填度数)
∵ b∥c
∴∠4 =∠2= ( ) (填度数)
( )
∠2 +∠3 =180° ( )
∴∠3 =180°-∠2 =( ) (填度数)
22.如图所示,直线AB与直线CD交于点O,OE⊥AB,OF平分∠AOC,若∠BOD=70°.你能否求出∠DOF的度数吗?
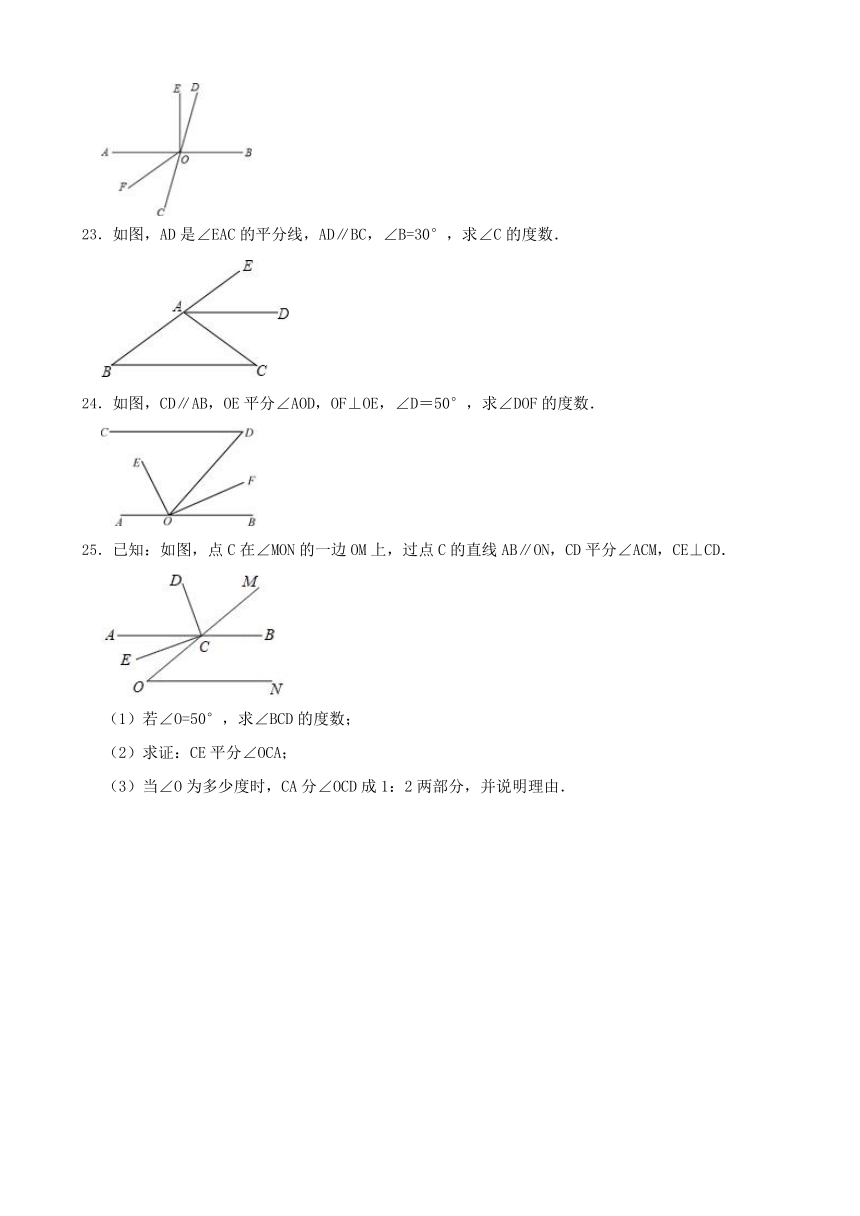
23.如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,求∠C的度数.
24.如图,CD∥AB,OE平分∠AOD,OF⊥OE,∠D=50°,求∠DOF的度数.
25.已知:如图,点C在∠MON的一边OM上,过点C的直线AB∥ON,CD平分∠ACM,CE⊥CD.
(1)若∠O=50°,求∠BCD的度数;
(2)求证:CE平分∠OCA;
(3)当∠O为多少度时,CA分∠OCD成1:2两部分,并说明理由.
答案
1.【答案】B
【解答】解:一个角的余角不一定比这个角大,如60°,①错误;
同角的余角相等,②正确;
两个角的和是180°,这两个角互补,所以互补是指两个角的关系,③错误;
对顶角相等,④正确,
故选:B.
【分析】根据余角和补角的概念、对顶角相等进行判断即可.
2.【答案】B
【解答】解:由一个角的两边的反向延长线是另一个角的两边,得
B中的图形∠1与∠2是对顶角,
故选:B.
【分析】根据对顶角的定义,可得答案.
3.【答案】D
【解答】解:
∵ ,
∴ ,
∴ .
故答案为:D.
【分析】对图形进行角标注,由平行线的性质可得∠3=∠1,然后根据邻补角的性质进行求解.
4.【答案】A
【解答】∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,
∴∠ABP=∠CBP=20°,∠ACP=∠MCP=50°,
∵∠PCM是△BCP的外角,
∴∠P=∠PCM ∠CBP=50° 20°=30°,
故答案为:A.
【分析】根据三角形的外角性质、角平分线的定义即可得出答案。
5.【答案】C
【分析】在同一平面内,若∠AOB=90 ,∠BOC=40 ,当OC在∠AOB内时,∠AOB的平分线与∠BOC 的平分线的夹角=45°-20°=25°;
当OC在∠AOB外时,∠AOB的平分线与∠BOC 的平分线的夹角=45°+20°=65 ,所以选C.
【点评】本题考查角平分线,要求学生掌握角平分线的概念和性质,利用角平分线的性质来解答本题。
6.【答案】B
【解答】A. 同位角只有在两直线平行时才相等,故不符合题意;
B. 垂线段最短,符合题意;
C. 相等的角不一定是对顶角,故不符合题意;
D. 互补的角不一定是邻补角,故不符合题意,
故答案为:B.
【分析】根据两直线的位置即可判断.
7.【答案】C
【解答】解:∵∠1=110°,∠3=∠1(对顶角相等),
∴∠3=110°,
又∵∠2=70°,
∴∠2+∠3=180°,
∴a∥b(同旁内角互补,两直线平行).
故答案为:C.
【分析】由对顶角相等可得∠3=∠1=110°,可得∠2+∠3=180°,根据同旁内角互补,两直线平行,可得a∥b.
8.【答案】A
【解答】设AB与DE交点为F点,∠AFE=∠BFD=180°-45°-90°=45°,
∠ABD=180°-∠ABC=75°,∴∠D=180°-75°-45°=60°
故答案为:A
【分析】根据对顶角相等以及余角的性质,可得出结果。
9.【答案】A
【分析】如图
∵直线a∥直线b,∠1=40°
∴∠3=∠1=40°
∴∠2=∠3=40°.
10.【答案】B
【解答】每两条直线相交构成2对对顶角,三条直线两两相交构成 对对顶角,故选B.
【分析】能够运用所学知识加以拓展,从而判断不同情况下对顶角的对数.
11.【答案】B
【解答】解:∵∠AOC为35°,
∴∠BOD=35°,
故选:B.
【分析】根据对顶角相等可得答案.
12.【答案】D
【解答】解:A、∠AOC与∠BOD是对顶角正确,故本选项错误;
B、∵OE⊥AB,
∴∠BOE=90°,
∴∠BOD和∠DOE互为余角正确,故本选项错误;
C、∵∠AOC=∠BOD(对顶角相等),∠BOD和∠DOE互为余角,
∴∠AOC和∠DOE互为余角正确,故本选项错误;
D、应为∠AOD和∠BOC是对顶角,故本选项正确.
故选D.
【分析】根据垂直的定义以及对顶角相等和互为余角的定义对各选项分析判断即可得解.
13.【答案】D
【解答】解:A、有公共顶点的两个角是对顶角错误,故本选项错误;
B、相等的角是对顶角错误,例如角平分线分成的两个角,故本选项错误;
C、有公共顶点且相等的角是对顶角错误,例如角平分线分成的两个角,故本选项错误;
D、对顶角相等正确,故本选项正确.
故选D.
【分析】根据对顶角的定义和对顶角相等的性质对各选项分析判断后利用排除法求解.
14.【答案】A
【解答】解: A、∠A与∠B是同旁内角,故说法符合题意;
B、 与 是邻补角,故说法不符合题意;
C、 与 是同位角,故说法不符合题意;
D、∠2与∠3是内错角,故说法不符合题意;
故答案为:A.
【分析】根据同位角、内错角、同旁内角以及对顶角的定义进行解答.
15.【答案】B
【解答】解:如图,
∵∠1=55°,
∴∠AFD=55°,
∴∠ADF=180°-45°-55°=80°,
∵MN∥HK,
∴∠AEG=∠ADF=80°,
∴∠2=80°-45°=35°.
故答案为:B.
【分析】对图形进行点标注,由对顶角的性质可得∠1=∠AFD=55°,然后由三角形内角和定理可得∠ADF的度数,接下来由平行线的性质可得∠AEG=∠ADF=80°,最后根据三角形外角的性质进行求解.
16.【答案】35°
【解答】解:∵直线AB,CD相交于点O,
∴∠AOC=∠BOD,
∵∠AOC=70°,
∴∠BOD=70°,
∵OE平分∠BOD,
∴∠EOD=35°;
故答案为35°.
【分析】由直线相交可知对顶角相等,即∠AOC=∠BOD,再由角平分线的性质可得∠EOD的度数.
17.【答案】146°23′
【解答】解:∵EO⊥AB于点O
∴∠EOA=90°
又∵∠EOD=56°23′
∴∠COB=∠AOD=∠EOD+∠EOA=90°+56°23′=146°23′
故答案为:146°23′
【分析】根据垂直的定义及角的和差算出∠AOD的度数,进而根据对顶角相等即可算出∠BOC的度数.
18.【答案】25°
【解答】解:根据定义∠A=65°的余角度数是90°﹣65°=25°,
故答案为:25°.
【分析】根据互余两角之和等于90°即可得出答案.
19.【答案】70°
【解答】解:如图所示:
根据题意得:∠1=∠2=∠3,
∵OC平分∠AOB,
∴∠AOC= ∠AOB=20°,
∴∠3=90°-20°=70°,
∴∠1=70°;
故答案为:B.
【分析】由平行线的性质和对顶角相等得出∠1=∠2=∠3,由角平分线的定义求出∠AOC= ∠AOB=20°,由直角三角形的性质求出∠3=70°,即可得出∠1的度数.
20.【答案】28°;152°
【解答】解:∵∠AOD=28°,
∴∠BOC=∠AOD=28°,
∠AOC=180°﹣∠AOD=180°﹣28°=152°.
故答案为:28°,152°.
【分析】根据对顶角相等和邻补角的定义列式解答.
21.【答案】解:∵∠1=∠2(对顶角相等),∠1+∠2=230°,
∴∠1=∠2=115°,
∵b∥c,
∴∠4=∠2=115°,(两直线平行,内错角相等),
∠2+∠3=180°,(两直线平行,同旁内角互补),
∴∠3=180°-∠2=65°
【分析】根据对顶角相等求出∠1和∠2,根据平行线的性质求出∠4=∠2,2+∠3=180°,代入求出即可.
22.【答案】解:∵∠BOD=70°,
∴ ∠AOC=∠BOD=70°,
又∵OF平分∠AOC
∴∠COF= ∠AOC=35°,
∴∠DOF=180°-∠COF=145°.
【分析】根据对顶角的性质,可得∠AOC的度数,根据角平分线的定义,可得∠COF的度数,根据角的和差,可得答案.
23.【答案】解:
∵AD∥BC,
∴∠1=∠B,
∠2=∠C,
又∵AD平分∠EAC,
∴∠1=∠2,
∴∠C=∠B=30°.
【分析】根据平行线的性质可得∠1=∠B,∠2=∠C,利用角平分线的定义∠1=∠2,利用等量代换即可求出∠C=∠B=30°.
24.【答案】解:∵CD∥AB∴
∵∴
∵OE平分∠AOD∴
∵OE⊥OF∴
∴
【分析】先根据两直线平行,同旁内角互补求出∠ AOD的度数,再根据角平分线的定义求出∠1的大小,接着根据垂直的定义求出∠2的大小,最后再根据平角的定义列式计算即可得解.
25.【答案】(1)解:∵AB∥ON,
∴∠O=∠MCB(两直线平行,同位角相等).
∵∠O=50°,
∴∠MCB=50°.
∵∠ACM+∠MCB=180°(平角定义),
∴∠ACM=180°-50°=130°.
又∵CD平分∠ACM,
∴∠DCM=65°(角平分线定义),
∴∠BCD=∠DCM+∠MCB=65°+50°=115°
(2)证明:∵CE⊥CD,
∴∠DCE=90°,
∴∠ACE+∠DCA=90°..
又∵∠MCO=180°(平角定义),
∴∠ECO+∠DCM=90°,
∵∠DCA =∠DCM,
∴∠ACE=∠ECO(等角的余角相等),
即CE平分∠OCA
(3)解:①当∠OCA: ∠ACD=1:2时,
设∠OCD=x°, ∠ACD=2x°,由题意得
x+2x+2x=180,
∴x=36,
∴∠O=∠OCA=x=36°;
②当∠ACD:∠OCA =1:2时,
设∠ACD =x°, ∠OCA =2x°,由题意得
x+x+2x=180,
∴x=45,
∴∠O=∠OCA=2x=2×45°=90°;
∴当∠O=36°或90°时,CA分∠OCD成1:2两部分
【分析】本题要应用平行线的性质,垂直的定义,角平分线的定义,一元一次方程的几何应用以及分类讨论的解题思路,涉及多个知识点,综合性较强,注意结合图形综合分析,找出解题思路。
一、填空题
1.下列说法中正确的有( )
①一个角的余角一定比这个角大;②同角的余角相等;③若∠1+∠2+∠3=180°,则∠1,∠2,∠3互补;④对顶角相等.
A.1个 B.2个 C.3个 D.4个
2.下列图形中,∠1与∠2是对顶角的是( )
A. B.
C. D.
3.已知平面内三条直线 与 相交,若 ,则 的度数为( )
A. B. C. D.
4.BP是∠ABC的平分线,CP是∠ACB的邻补角的平分线,∠ABP=20°,∠ACP=50°,则∠P=( )
A.30° B.40° C.50° D.60°
5.在同一平面内,若∠AOB=90 ,∠BOC=40 ,则∠AOB的平分线与∠BOC 的平分线的夹角等于( )
A.65 B.25 C.65 或25 D.60 或20
6.下列命题中真命题是( )
A.同位角相等 B.垂线段最短
C.相等的角是对顶角 D.互补的角是邻补角
7.已知:如图,,,求证:∥.下面为嘉琪同学的证明过程:
证明:∵,( ① ),
∴.又∵,∴
∴∥( ② ).
其中①②为解题依据,则下列描述正确的是( )
A.①代表内错角相等
B.②代表同位角相等,两直线平行
C.①代表对顶角相等
D.②代表同旁内角相等,两直线平行
8.如图,已知△ABC中,∠A=45°,∠ABC=105°,在CB延长线上有一点D,过点D作DE⊥AC于点E,则∠D=( )
A.60° B.65° C.70° D.75°
9.如图,若直线a∥直线b,∠1=40°,则∠2的度数为( )
A.40° B.50° C.140° D.160°
10.平面上三条直线两两相交最多能构成对顶角的对数是( ).
A.7 B.6 C.5 D.4
11.直线AB、CD交于点O,若∠AOC为35°,则∠BOD的度数为( )
A.30° B.35° C.55° D.145°
12.如图AB、CD交于点O,OE⊥AB于O,则下列不正确的是( )
A.∠AOC与∠BOD是对顶角 B.∠BOD和∠DOE互为余角
C.∠AOC和∠DOE互为余角 D.∠AOE和∠BOC是对顶角
13.下列说法正确的是( )
A.有公共顶点的两个角是对顶角
B.相等的角是对顶角
C.有公共顶点且相等的角是对顶角
D.对顶角相等
14.如图,下列说法正确的是( )
A. 与 是同旁内角 B. 与 是对顶角
C. 与 是内错角 D. 与 是同位角
15.一块含有45°的直角三角板和直尺如图放置,若∠1=55°,则∠2的度数是( )
A.30° B.35° C.40° D.45°
二、填空题
16.如图所示,直线AB,CD相交于点O,已知∠AOC=70°,OE平分∠BOD,则∠EOD= .
17.如图,直线AB,CD相交于点O,EO⊥AB于点O,∠EOD=56°23′,则∠BOC的度数为 .
18.已知∠A=65°,则∠A的余角是
19.如图, , 平分 ,直尺与 垂直,则∠1等于 .
20.如图,直线AB、CD相交于点O,若∠AOD=28°,则∠BOC= ,∠AOC= .
三、解答题
21.说明理由
如图,∠1+∠2=230°,b∥c, 则∠1、∠2、∠3、∠4各是多少度?
解:∵ ∠1=∠2 ( )
∠1+∠2=230°
∴∠1 =∠2 =( ) (填度数)
∵ b∥c
∴∠4 =∠2= ( ) (填度数)
( )
∠2 +∠3 =180° ( )
∴∠3 =180°-∠2 =( ) (填度数)
22.如图所示,直线AB与直线CD交于点O,OE⊥AB,OF平分∠AOC,若∠BOD=70°.你能否求出∠DOF的度数吗?
23.如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,求∠C的度数.
24.如图,CD∥AB,OE平分∠AOD,OF⊥OE,∠D=50°,求∠DOF的度数.
25.已知:如图,点C在∠MON的一边OM上,过点C的直线AB∥ON,CD平分∠ACM,CE⊥CD.
(1)若∠O=50°,求∠BCD的度数;
(2)求证:CE平分∠OCA;
(3)当∠O为多少度时,CA分∠OCD成1:2两部分,并说明理由.
答案
1.【答案】B
【解答】解:一个角的余角不一定比这个角大,如60°,①错误;
同角的余角相等,②正确;
两个角的和是180°,这两个角互补,所以互补是指两个角的关系,③错误;
对顶角相等,④正确,
故选:B.
【分析】根据余角和补角的概念、对顶角相等进行判断即可.
2.【答案】B
【解答】解:由一个角的两边的反向延长线是另一个角的两边,得
B中的图形∠1与∠2是对顶角,
故选:B.
【分析】根据对顶角的定义,可得答案.
3.【答案】D
【解答】解:
∵ ,
∴ ,
∴ .
故答案为:D.
【分析】对图形进行角标注,由平行线的性质可得∠3=∠1,然后根据邻补角的性质进行求解.
4.【答案】A
【解答】∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,
∴∠ABP=∠CBP=20°,∠ACP=∠MCP=50°,
∵∠PCM是△BCP的外角,
∴∠P=∠PCM ∠CBP=50° 20°=30°,
故答案为:A.
【分析】根据三角形的外角性质、角平分线的定义即可得出答案。
5.【答案】C
【分析】在同一平面内,若∠AOB=90 ,∠BOC=40 ,当OC在∠AOB内时,∠AOB的平分线与∠BOC 的平分线的夹角=45°-20°=25°;
当OC在∠AOB外时,∠AOB的平分线与∠BOC 的平分线的夹角=45°+20°=65 ,所以选C.
【点评】本题考查角平分线,要求学生掌握角平分线的概念和性质,利用角平分线的性质来解答本题。
6.【答案】B
【解答】A. 同位角只有在两直线平行时才相等,故不符合题意;
B. 垂线段最短,符合题意;
C. 相等的角不一定是对顶角,故不符合题意;
D. 互补的角不一定是邻补角,故不符合题意,
故答案为:B.
【分析】根据两直线的位置即可判断.
7.【答案】C
【解答】解:∵∠1=110°,∠3=∠1(对顶角相等),
∴∠3=110°,
又∵∠2=70°,
∴∠2+∠3=180°,
∴a∥b(同旁内角互补,两直线平行).
故答案为:C.
【分析】由对顶角相等可得∠3=∠1=110°,可得∠2+∠3=180°,根据同旁内角互补,两直线平行,可得a∥b.
8.【答案】A
【解答】设AB与DE交点为F点,∠AFE=∠BFD=180°-45°-90°=45°,
∠ABD=180°-∠ABC=75°,∴∠D=180°-75°-45°=60°
故答案为:A
【分析】根据对顶角相等以及余角的性质,可得出结果。
9.【答案】A
【分析】如图
∵直线a∥直线b,∠1=40°
∴∠3=∠1=40°
∴∠2=∠3=40°.
10.【答案】B
【解答】每两条直线相交构成2对对顶角,三条直线两两相交构成 对对顶角,故选B.
【分析】能够运用所学知识加以拓展,从而判断不同情况下对顶角的对数.
11.【答案】B
【解答】解:∵∠AOC为35°,
∴∠BOD=35°,
故选:B.
【分析】根据对顶角相等可得答案.
12.【答案】D
【解答】解:A、∠AOC与∠BOD是对顶角正确,故本选项错误;
B、∵OE⊥AB,
∴∠BOE=90°,
∴∠BOD和∠DOE互为余角正确,故本选项错误;
C、∵∠AOC=∠BOD(对顶角相等),∠BOD和∠DOE互为余角,
∴∠AOC和∠DOE互为余角正确,故本选项错误;
D、应为∠AOD和∠BOC是对顶角,故本选项正确.
故选D.
【分析】根据垂直的定义以及对顶角相等和互为余角的定义对各选项分析判断即可得解.
13.【答案】D
【解答】解:A、有公共顶点的两个角是对顶角错误,故本选项错误;
B、相等的角是对顶角错误,例如角平分线分成的两个角,故本选项错误;
C、有公共顶点且相等的角是对顶角错误,例如角平分线分成的两个角,故本选项错误;
D、对顶角相等正确,故本选项正确.
故选D.
【分析】根据对顶角的定义和对顶角相等的性质对各选项分析判断后利用排除法求解.
14.【答案】A
【解答】解: A、∠A与∠B是同旁内角,故说法符合题意;
B、 与 是邻补角,故说法不符合题意;
C、 与 是同位角,故说法不符合题意;
D、∠2与∠3是内错角,故说法不符合题意;
故答案为:A.
【分析】根据同位角、内错角、同旁内角以及对顶角的定义进行解答.
15.【答案】B
【解答】解:如图,
∵∠1=55°,
∴∠AFD=55°,
∴∠ADF=180°-45°-55°=80°,
∵MN∥HK,
∴∠AEG=∠ADF=80°,
∴∠2=80°-45°=35°.
故答案为:B.
【分析】对图形进行点标注,由对顶角的性质可得∠1=∠AFD=55°,然后由三角形内角和定理可得∠ADF的度数,接下来由平行线的性质可得∠AEG=∠ADF=80°,最后根据三角形外角的性质进行求解.
16.【答案】35°
【解答】解:∵直线AB,CD相交于点O,
∴∠AOC=∠BOD,
∵∠AOC=70°,
∴∠BOD=70°,
∵OE平分∠BOD,
∴∠EOD=35°;
故答案为35°.
【分析】由直线相交可知对顶角相等,即∠AOC=∠BOD,再由角平分线的性质可得∠EOD的度数.
17.【答案】146°23′
【解答】解:∵EO⊥AB于点O
∴∠EOA=90°
又∵∠EOD=56°23′
∴∠COB=∠AOD=∠EOD+∠EOA=90°+56°23′=146°23′
故答案为:146°23′
【分析】根据垂直的定义及角的和差算出∠AOD的度数,进而根据对顶角相等即可算出∠BOC的度数.
18.【答案】25°
【解答】解:根据定义∠A=65°的余角度数是90°﹣65°=25°,
故答案为:25°.
【分析】根据互余两角之和等于90°即可得出答案.
19.【答案】70°
【解答】解:如图所示:
根据题意得:∠1=∠2=∠3,
∵OC平分∠AOB,
∴∠AOC= ∠AOB=20°,
∴∠3=90°-20°=70°,
∴∠1=70°;
故答案为:B.
【分析】由平行线的性质和对顶角相等得出∠1=∠2=∠3,由角平分线的定义求出∠AOC= ∠AOB=20°,由直角三角形的性质求出∠3=70°,即可得出∠1的度数.
20.【答案】28°;152°
【解答】解:∵∠AOD=28°,
∴∠BOC=∠AOD=28°,
∠AOC=180°﹣∠AOD=180°﹣28°=152°.
故答案为:28°,152°.
【分析】根据对顶角相等和邻补角的定义列式解答.
21.【答案】解:∵∠1=∠2(对顶角相等),∠1+∠2=230°,
∴∠1=∠2=115°,
∵b∥c,
∴∠4=∠2=115°,(两直线平行,内错角相等),
∠2+∠3=180°,(两直线平行,同旁内角互补),
∴∠3=180°-∠2=65°
【分析】根据对顶角相等求出∠1和∠2,根据平行线的性质求出∠4=∠2,2+∠3=180°,代入求出即可.
22.【答案】解:∵∠BOD=70°,
∴ ∠AOC=∠BOD=70°,
又∵OF平分∠AOC
∴∠COF= ∠AOC=35°,
∴∠DOF=180°-∠COF=145°.
【分析】根据对顶角的性质,可得∠AOC的度数,根据角平分线的定义,可得∠COF的度数,根据角的和差,可得答案.
23.【答案】解:
∵AD∥BC,
∴∠1=∠B,
∠2=∠C,
又∵AD平分∠EAC,
∴∠1=∠2,
∴∠C=∠B=30°.
【分析】根据平行线的性质可得∠1=∠B,∠2=∠C,利用角平分线的定义∠1=∠2,利用等量代换即可求出∠C=∠B=30°.
24.【答案】解:∵CD∥AB∴
∵∴
∵OE平分∠AOD∴
∵OE⊥OF∴
∴
【分析】先根据两直线平行,同旁内角互补求出∠ AOD的度数,再根据角平分线的定义求出∠1的大小,接着根据垂直的定义求出∠2的大小,最后再根据平角的定义列式计算即可得解.
25.【答案】(1)解:∵AB∥ON,
∴∠O=∠MCB(两直线平行,同位角相等).
∵∠O=50°,
∴∠MCB=50°.
∵∠ACM+∠MCB=180°(平角定义),
∴∠ACM=180°-50°=130°.
又∵CD平分∠ACM,
∴∠DCM=65°(角平分线定义),
∴∠BCD=∠DCM+∠MCB=65°+50°=115°
(2)证明:∵CE⊥CD,
∴∠DCE=90°,
∴∠ACE+∠DCA=90°..
又∵∠MCO=180°(平角定义),
∴∠ECO+∠DCM=90°,
∵∠DCA =∠DCM,
∴∠ACE=∠ECO(等角的余角相等),
即CE平分∠OCA
(3)解:①当∠OCA: ∠ACD=1:2时,
设∠OCD=x°, ∠ACD=2x°,由题意得
x+2x+2x=180,
∴x=36,
∴∠O=∠OCA=x=36°;
②当∠ACD:∠OCA =1:2时,
设∠ACD =x°, ∠OCA =2x°,由题意得
x+x+2x=180,
∴x=45,
∴∠O=∠OCA=2x=2×45°=90°;
∴当∠O=36°或90°时,CA分∠OCD成1:2两部分
【分析】本题要应用平行线的性质,垂直的定义,角平分线的定义,一元一次方程的几何应用以及分类讨论的解题思路,涉及多个知识点,综合性较强,注意结合图形综合分析,找出解题思路。
