【慧学智评】北师大版九上数学 4-7 三角形相似条件3 同步授课课件
文档属性
| 名称 | 【慧学智评】北师大版九上数学 4-7 三角形相似条件3 同步授课课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-14 11:37:00 | ||
图片预览




文档简介
(共11张PPT)
第四章
图形的相似
第36课
三角形相似条件(3)
C
F
E
A
D
B
①
C
F
E
A
D
B
②
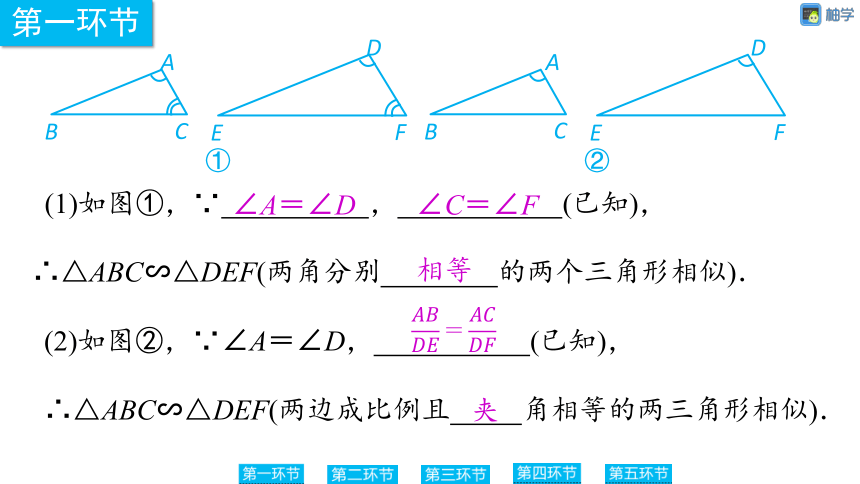
(1)如图①,∵%// //%,%// //%(已知),
∴△ABC∽△DEF(两角分别%// //%的两个三角形相似).
(2)如图②,∵∠A=∠D,%// //%(已知),
∴△ABC∽△DEF(两边成比例且%///%角相等的两三角形相似).
∠A=∠D
∠C=∠F
相等
夹
(3)如果两个三角形的三边成比例,那么这个三角形一定相似吗?
解:如果两个三角形的三边成比例,那么这个三角形一定相似.
【问题 1】在图中画 与 , 使得 都等于 3. 设法比较 与 的大小. 与 相似吗 说说你的理由.
解: 与 相似. 图略.
【问题 2】若 都等于 或其他任意值 , 是否会有同样的结果
解:是的
归纳结论:三边 的两个三角形相似.
定理: 成比例的两个三角形相似.
几何语言 :如图 , (已知),
三边成比例的两个三角形相似 .
成比例
三边
BC
DF
F
E
D
C
A
B
C
3.5
2.5
A
3
B
F
4.2
3
D
3.6
E
例题1图
【例题1】判断下列每组三角形是否相似. (填“相似”或“不相似”)
两个三角形的边长分别为 和 . ( )
(2) 如图, 与 . ( )
相似
相似
C
E
A
D
B
例题2图
【例题2】如图,在△ABC和△ADE中,==,∠BAD=20°,求∠CAE的度数.
解:∵在△ABC和△ADE中,
==,
∴△ABC∽△ADE,
∴∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠CAE=∠BAD=20°.
1.在△ABC和△A1B1C1中,AB∶AC∶BC=4∶3∶2,A1B1∶A1C1∶B1C1=3∶2∶4.则△ABC与△A1B1C1.
是否相似·······································(%// //%)
A.一定相似 B.一定不相似
C.不一定相似 D.无法判断
A
C
F
E
A
D
B
G
K
H
④
⑤
⑥
③
②
①
第2题图
2.如图,在正方形网格上有6个三角形①△ABC,②△BCD,③△BDE,④△BFG,⑤△FGH,⑥△EFK,其中②~⑥中与三角形①相似的有%// //%.
③④⑤
C
F
E
A
D
B
第3题图
3.(★)【中考真题】如图4-7-8,点B、D、E在一条直线上,BE与AC相交于点F,且==,连接EC .
(1)求证:△ABD∽△ACE;
(2)若∠BAD=21°,
求∠EBC的度数.
(1)证明:∵==,
∴△ABC∽△ADE,∴∠BAC=∠DAE,
∴∠BAC-∠DAF=∠DAE-∠DAF,即∠BAD=∠CAE,
∵=,∴△ABD∽△ACE.
(2)解:∵△ABC∽△ADE,∴∠ABC=∠ADE,
∵∠ABC=∠ABE+∠EBC,∠ADE=∠ABE+∠BAD,
∴∠EBC=∠BAD=21°.
第四章
图形的相似
第36课
三角形相似条件(3)
C
F
E
A
D
B
①
C
F
E
A
D
B
②
(1)如图①,∵%// //%,%// //%(已知),
∴△ABC∽△DEF(两角分别%// //%的两个三角形相似).
(2)如图②,∵∠A=∠D,%// //%(已知),
∴△ABC∽△DEF(两边成比例且%///%角相等的两三角形相似).
∠A=∠D
∠C=∠F
相等
夹
(3)如果两个三角形的三边成比例,那么这个三角形一定相似吗?
解:如果两个三角形的三边成比例,那么这个三角形一定相似.
【问题 1】在图中画 与 , 使得 都等于 3. 设法比较 与 的大小. 与 相似吗 说说你的理由.
解: 与 相似. 图略.
【问题 2】若 都等于 或其他任意值 , 是否会有同样的结果
解:是的
归纳结论:三边 的两个三角形相似.
定理: 成比例的两个三角形相似.
几何语言 :如图 , (已知),
三边成比例的两个三角形相似 .
成比例
三边
BC
DF
F
E
D
C
A
B
C
3.5
2.5
A
3
B
F
4.2
3
D
3.6
E
例题1图
【例题1】判断下列每组三角形是否相似. (填“相似”或“不相似”)
两个三角形的边长分别为 和 . ( )
(2) 如图, 与 . ( )
相似
相似
C
E
A
D
B
例题2图
【例题2】如图,在△ABC和△ADE中,==,∠BAD=20°,求∠CAE的度数.
解:∵在△ABC和△ADE中,
==,
∴△ABC∽△ADE,
∴∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠CAE=∠BAD=20°.
1.在△ABC和△A1B1C1中,AB∶AC∶BC=4∶3∶2,A1B1∶A1C1∶B1C1=3∶2∶4.则△ABC与△A1B1C1.
是否相似·······································(%// //%)
A.一定相似 B.一定不相似
C.不一定相似 D.无法判断
A
C
F
E
A
D
B
G
K
H
④
⑤
⑥
③
②
①
第2题图
2.如图,在正方形网格上有6个三角形①△ABC,②△BCD,③△BDE,④△BFG,⑤△FGH,⑥△EFK,其中②~⑥中与三角形①相似的有%// //%.
③④⑤
C
F
E
A
D
B
第3题图
3.(★)【中考真题】如图4-7-8,点B、D、E在一条直线上,BE与AC相交于点F,且==,连接EC .
(1)求证:△ABD∽△ACE;
(2)若∠BAD=21°,
求∠EBC的度数.
(1)证明:∵==,
∴△ABC∽△ADE,∴∠BAC=∠DAE,
∴∠BAC-∠DAF=∠DAE-∠DAF,即∠BAD=∠CAE,
∵=,∴△ABD∽△ACE.
(2)解:∵△ABC∽△ADE,∴∠ABC=∠ADE,
∵∠ABC=∠ABE+∠EBC,∠ADE=∠ABE+∠BAD,
∴∠EBC=∠BAD=21°.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
