【慧学智评】北师大版九上数学 4-11 相似三角形性质2 同步授课课件
文档属性
| 名称 | 【慧学智评】北师大版九上数学 4-11 相似三角形性质2 同步授课课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-14 11:37:00 | ||
图片预览





文档简介
(共17张PPT)
第四章
图形的相似
第40课
相似三角形性质(2)
(1)两个相似三角形的%// //%相等,
%// //%成比例.
(2)两个相似三角形%// //%、
%// //%、
%// //%都等于相似比.
对应角
对应边
对应高的比
对应角平分线的比
对应中线的比
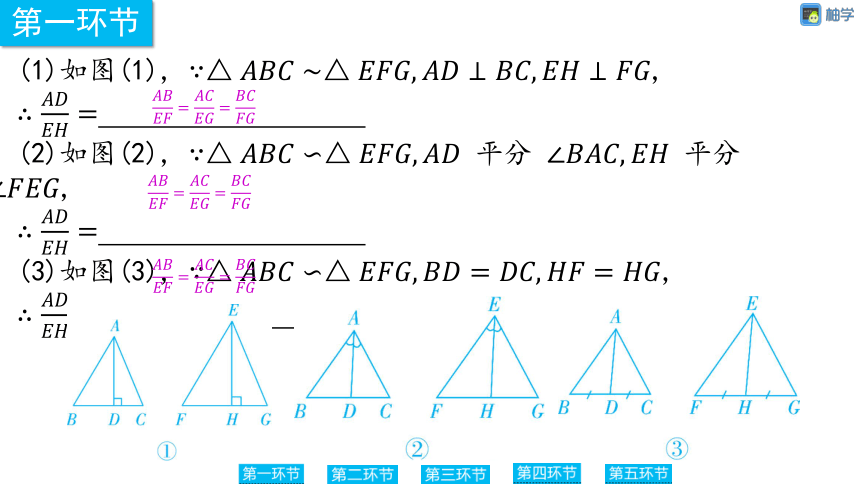
(1)如图(1), ,
(2)如图(2), 平分 平分 ,
(3)如图(3), ,
C
B′
A′
A
D
B
D′
C′
如图,△ABC∽△A′B′C′,相似比为2,
AD、A′D′分别是这两个三角形的高.
【问题1】请写出相似三角形的三对对应边的比及其比值.
【问题2】请写出对应高之比及其比值.
===2
=2
【问题3】这两个三角形的周长比是%// //%;
这两个三角形的面积比是%// //%;
然后说明理由.
==2;
==22=4.
2
4
C
B′
A′
A
D
B
D′
C′
问题4图
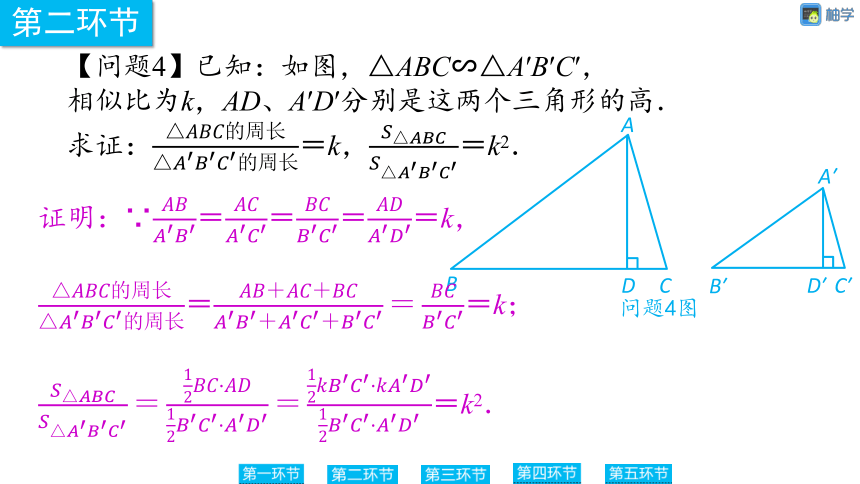
【问题4】已知:如图,△ABC∽△A′B′C′,
相似比为k,AD、A′D′分别是这两个三角形的高.
求证:=k,=k2.
证明:∵====k,
==k;
=k2.
定理:
相似三角形的 等于%// //%;
等于%// //%.
周长比
相似比
面积比
相似比的平方
【问题5】(1)两个相似四边形的周长的比等于相似比吗?面积比等于相似比的平方吗?
(2)两个相似五边形的周长的比以及面积的比怎样呢?两个相似的n边形呢?
两个相似四边形的周长的比等于相似比,面积比等于相似比的平方.
两个相似五边形的周长的比等于相似比,面积比等于相似比的平方;两个相似的n边形也成立.
C
F
E
A
D
B
例题1图
【例题1】如图,在□ABCD中,E是AB上一点且BE=2AE,连接AC、DE交于点F.
(1)若AF=2,则AC的长为%// //%;
(2)若△CDF的面积为9 cm2,
则△AEF的面积为%// //%,
□ABCD的面积为%// //% cm2.
6
1
24
C
F
E
A
D
B
G
例题2图
【例题2】如图,将△ABC沿BC方向平移得到△DEF,△ABC与△DEF重叠部分(图中阴影部分)的面积与四边形ABEG的面积相等.已知BC=2,求△ABC平移的距离.
解:由题意知△ECG的面积等于四边形ABEG的面积,
∴S△ABC=2S△GEC,由平移得AB∥EG,
∴△ABC∽△ECG,
∴=()2=2,解得CE=,
由图知△ABC平移的距离是CF,且CF=BE=2-.
1.两个相似三角形,两个相似三角形的面积比是4∶3,
则其周长比是%// //%.
2∶
2.两个相似三角形周长的比是2∶3,它们的面积差是25,则较大的三角形的面积是 (%// //%)
A.75 B.65 C.50 D.45
D
C
F
E
A
D
B
第3题图
3.如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE=2ED,则下列结论错误的是 (%// //%)
A.EF=2CE
B.S△AEF=S△BCF
C.BF=3CD
D.BC=AE
B
C
F
E
A
D
B
第4题图
4.(★)【中考真题】如图,在四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,AC交DE于点F.
(1)求证:AC2=AB·AD;
(2)若AD=4,AB=6,
求的值.
(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB.
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴=,即AC2=AB·AD.
(2)解:∵∠ACB=90°,E为AB的中点,
∴CE=AE=AB=3,
∴∠CAE=∠ACE,
∴∠CEB=∠CAE+∠ACE=2∠CAE=∠DAB,
∴CE∥AD,
∴△ADF∽△CEF,
∴=()2=()2=.
第四章
图形的相似
第40课
相似三角形性质(2)
(1)两个相似三角形的%// //%相等,
%// //%成比例.
(2)两个相似三角形%// //%、
%// //%、
%// //%都等于相似比.
对应角
对应边
对应高的比
对应角平分线的比
对应中线的比
(1)如图(1), ,
(2)如图(2), 平分 平分 ,
(3)如图(3), ,
C
B′
A′
A
D
B
D′
C′
如图,△ABC∽△A′B′C′,相似比为2,
AD、A′D′分别是这两个三角形的高.
【问题1】请写出相似三角形的三对对应边的比及其比值.
【问题2】请写出对应高之比及其比值.
===2
=2
【问题3】这两个三角形的周长比是%// //%;
这两个三角形的面积比是%// //%;
然后说明理由.
==2;
==22=4.
2
4
C
B′
A′
A
D
B
D′
C′
问题4图
【问题4】已知:如图,△ABC∽△A′B′C′,
相似比为k,AD、A′D′分别是这两个三角形的高.
求证:=k,=k2.
证明:∵====k,
==k;
=k2.
定理:
相似三角形的 等于%// //%;
等于%// //%.
周长比
相似比
面积比
相似比的平方
【问题5】(1)两个相似四边形的周长的比等于相似比吗?面积比等于相似比的平方吗?
(2)两个相似五边形的周长的比以及面积的比怎样呢?两个相似的n边形呢?
两个相似四边形的周长的比等于相似比,面积比等于相似比的平方.
两个相似五边形的周长的比等于相似比,面积比等于相似比的平方;两个相似的n边形也成立.
C
F
E
A
D
B
例题1图
【例题1】如图,在□ABCD中,E是AB上一点且BE=2AE,连接AC、DE交于点F.
(1)若AF=2,则AC的长为%// //%;
(2)若△CDF的面积为9 cm2,
则△AEF的面积为%// //%,
□ABCD的面积为%// //% cm2.
6
1
24
C
F
E
A
D
B
G
例题2图
【例题2】如图,将△ABC沿BC方向平移得到△DEF,△ABC与△DEF重叠部分(图中阴影部分)的面积与四边形ABEG的面积相等.已知BC=2,求△ABC平移的距离.
解:由题意知△ECG的面积等于四边形ABEG的面积,
∴S△ABC=2S△GEC,由平移得AB∥EG,
∴△ABC∽△ECG,
∴=()2=2,解得CE=,
由图知△ABC平移的距离是CF,且CF=BE=2-.
1.两个相似三角形,两个相似三角形的面积比是4∶3,
则其周长比是%// //%.
2∶
2.两个相似三角形周长的比是2∶3,它们的面积差是25,则较大的三角形的面积是 (%// //%)
A.75 B.65 C.50 D.45
D
C
F
E
A
D
B
第3题图
3.如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE=2ED,则下列结论错误的是 (%// //%)
A.EF=2CE
B.S△AEF=S△BCF
C.BF=3CD
D.BC=AE
B
C
F
E
A
D
B
第4题图
4.(★)【中考真题】如图,在四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,AC交DE于点F.
(1)求证:AC2=AB·AD;
(2)若AD=4,AB=6,
求的值.
(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB.
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴=,即AC2=AB·AD.
(2)解:∵∠ACB=90°,E为AB的中点,
∴CE=AE=AB=3,
∴∠CAE=∠ACE,
∴∠CEB=∠CAE+∠ACE=2∠CAE=∠DAB,
∴CE∥AD,
∴△ADF∽△CEF,
∴=()2=()2=.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
