【慧学智评】北师大版九上数学 4-10 相似三角形性质1 同步授课课件
文档属性
| 名称 | 【慧学智评】北师大版九上数学 4-10 相似三角形性质1 同步授课课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-14 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
第四章
图形的相似
第39课
相似三角形性质(1)
(1)相似三角形的性质:
(2)三角形相似的判定:
定理1:
定理2:
定理3:
相似三角形的对应角相等,对应边成比例
两角分别相等的两个三角形相似
两边成比例且夹角相等的两个三角形相似
三边成比例的两个三角形相似
C
A
D
B
C′
A′
D′
B′
问题1图
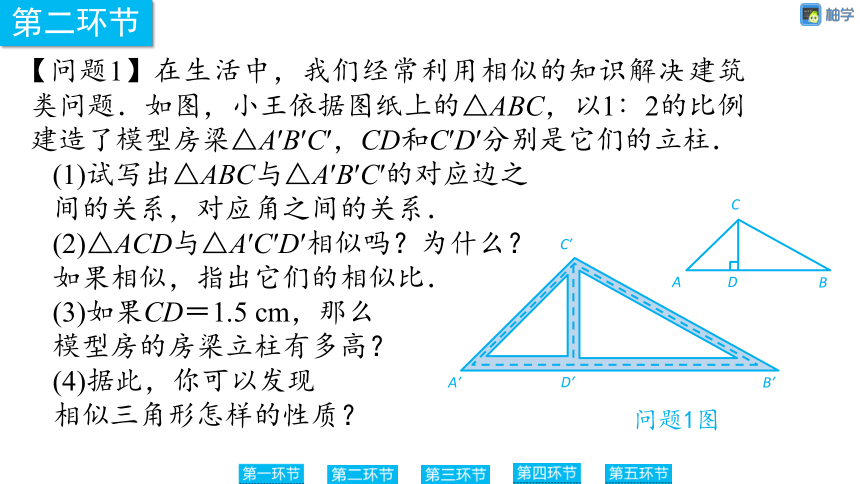
【问题1】在生活中,我们经常利用相似的知识解决建筑类问题.如图,小王依据图纸上的△ABC,以1∶2的比例建造了模型房梁△A′B′C′,CD和C′D′分别是它们的立柱.
(1)试写出△ABC与△A′B′C′的对应边之
间的关系,对应角之间的关系.
(2)△ACD与△A′C′D′相似吗?为什么?
如果相似,指出它们的相似比.
(3)如果CD=1.5 cm,那么
模型房的房梁立柱有多高?
(4)据此,你可以发现
相似三角形怎样的性质?
解:(1)由题意知它们的对应边成比例,对应角相等;
(2)△ACD与△A′C′D′相似,理由:
∵∠B=∠B′,CD⊥AB,C′D′⊥A′B′,
∴△ACD∽△A′C′D′;相似比是AC∶A′C′=1∶2.
(3)易知CD∶C′D′=1∶2,∴模型房的房梁立柱高是3 cm
(4)相似三角形对应高的比等于相似比.
C
B′
A′
A
D
B
D′
C′
问题2图
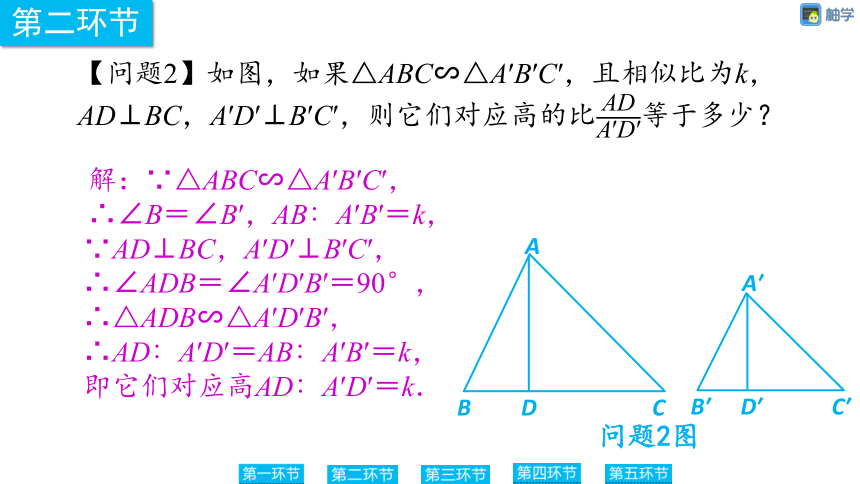
【问题2】如图,如果△ABC∽△A′B′C′,且相似比为k,AD⊥BC,A′D′⊥B′C′,则它们对应高的比等于多少?
解:∵△ABC∽△A′B′C′,
∴∠B=∠B′,AB∶A′B′=k,
∵AD⊥BC,A′D′⊥B′C′,
∴∠ADB=∠A′D′B′=90°,
∴△ADB∽△A′D′B′,
∴AD∶A′D′=AB∶A′B′=k,
即它们对应高AD∶A′D′=k.
C
E
A
D
B
C′
E′
A′
D′
B′
问题3图
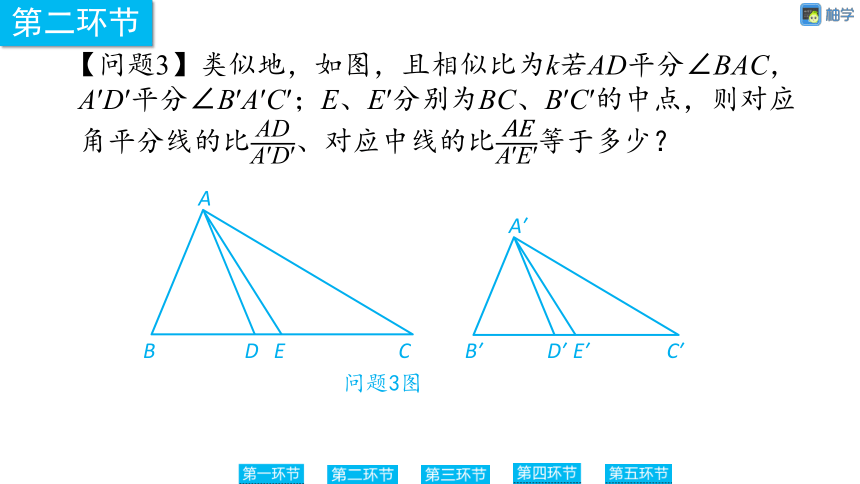
【问题3】类似地,如图,且相似比为k若AD平分∠BAC,A′D′平分∠B′A′C′;E、E′分别为BC、B′C′的中点,则对应角平分线的比、对应中线的比等于多少?
解:①∵△ABC∽△A′B′C′,
∴∠B=∠B′,∠BAC=∠B′A′C′,AB∶A′B′=k,
∵AD平分∠BAC,A′D′平分∠B′A′C′,
∴∠BAD=∠BAC,∠B′A′D′=∠B′A′C′,
∴∠BAD=∠B′A′D′,
∴△ADB∽△A′D′B′,
∴AD∶A′D′=AB∶A′B′=k;
②∵△ABC∽△A′B′C′,AB∶A′B′=BC∶B′C′=k,
∵E、E′分别为BC、B′C′的中点,
∴BE=BC,B′E′=B′C′,
∴BE∶B′E′=BC∶B′C′=k,
∴AD∶A′D′=BE∶B′E′=k.
小结:
两个相似三角形%// //%、
%// //%、
%// //%都等于相似比.
对应高的比
对应角平分线的比
对应中线的比
C
E
A
D
B
C′
E′
A′
D′
B′
例题1图
【例题1】如图,△ABC∽△A′B′C′,AD、BE分别是△ABC的高和中线,A′D′、B′E′分别是△A′B′C′的高和中线,且AD=12,A′D′=9,DE=6.5,求C′D′的长.
解:∵△ABC∽△A′B′C′,∴∠C=∠C′,
又∵AD与A′D′分别是高线,∴△ADC∽△A′D′C′,
∵E与E′分别是AC与A′C′的中点,
由AD=12,A′D′=9,DE=6.5,
∴AC=2DE=13,∴DC=5,
∵AD∶A′D′=DC∶D′C′,
∴D′C′=.
例题2图
C
B
O
A
D
【例题2】如图,小强自制了一个小孔成像装置,其中纸筒的长度为15 cm.他准备了一支长为20 cm的蜡烛,想要得到高度为5 cm的像,蜡烛应放在距离纸筒%// //% cm的地方.
60
1.已知△ABC∽△A′B′C′.若BD和B′D′是它们的对应角平分线,=,B′D′=4,则BD=%// //%.
6
C
E
A
D
B
第2题图
2.如图,在△ABC中AB=5,D,E分别是边AC和AB上的点,且∠ADE=∠B,DE=2,则AD·BC的值为%// //%.
10
y
O
x
C
A
D
B
第3题图
3.如图,点O为坐标原点,点A、B的坐标分别为(9,0)、(6,9),AB延长线一点C的坐标为(5,12),作CD∥BO交x轴于点D,则点D的坐标为%// .
(-3,0)
4.(☆) 如图, 点 在线段 上, 是等边三角形, 且 .
(1) 求 的大小.
(2) 说明线段 之间的数量关系.
解: (1) 是等边三角形,
,
,
,
.
(2) 是等边三角形,
.
,
,
.
第四章
图形的相似
第39课
相似三角形性质(1)
(1)相似三角形的性质:
(2)三角形相似的判定:
定理1:
定理2:
定理3:
相似三角形的对应角相等,对应边成比例
两角分别相等的两个三角形相似
两边成比例且夹角相等的两个三角形相似
三边成比例的两个三角形相似
C
A
D
B
C′
A′
D′
B′
问题1图
【问题1】在生活中,我们经常利用相似的知识解决建筑类问题.如图,小王依据图纸上的△ABC,以1∶2的比例建造了模型房梁△A′B′C′,CD和C′D′分别是它们的立柱.
(1)试写出△ABC与△A′B′C′的对应边之
间的关系,对应角之间的关系.
(2)△ACD与△A′C′D′相似吗?为什么?
如果相似,指出它们的相似比.
(3)如果CD=1.5 cm,那么
模型房的房梁立柱有多高?
(4)据此,你可以发现
相似三角形怎样的性质?
解:(1)由题意知它们的对应边成比例,对应角相等;
(2)△ACD与△A′C′D′相似,理由:
∵∠B=∠B′,CD⊥AB,C′D′⊥A′B′,
∴△ACD∽△A′C′D′;相似比是AC∶A′C′=1∶2.
(3)易知CD∶C′D′=1∶2,∴模型房的房梁立柱高是3 cm
(4)相似三角形对应高的比等于相似比.
C
B′
A′
A
D
B
D′
C′
问题2图
【问题2】如图,如果△ABC∽△A′B′C′,且相似比为k,AD⊥BC,A′D′⊥B′C′,则它们对应高的比等于多少?
解:∵△ABC∽△A′B′C′,
∴∠B=∠B′,AB∶A′B′=k,
∵AD⊥BC,A′D′⊥B′C′,
∴∠ADB=∠A′D′B′=90°,
∴△ADB∽△A′D′B′,
∴AD∶A′D′=AB∶A′B′=k,
即它们对应高AD∶A′D′=k.
C
E
A
D
B
C′
E′
A′
D′
B′
问题3图
【问题3】类似地,如图,且相似比为k若AD平分∠BAC,A′D′平分∠B′A′C′;E、E′分别为BC、B′C′的中点,则对应角平分线的比、对应中线的比等于多少?
解:①∵△ABC∽△A′B′C′,
∴∠B=∠B′,∠BAC=∠B′A′C′,AB∶A′B′=k,
∵AD平分∠BAC,A′D′平分∠B′A′C′,
∴∠BAD=∠BAC,∠B′A′D′=∠B′A′C′,
∴∠BAD=∠B′A′D′,
∴△ADB∽△A′D′B′,
∴AD∶A′D′=AB∶A′B′=k;
②∵△ABC∽△A′B′C′,AB∶A′B′=BC∶B′C′=k,
∵E、E′分别为BC、B′C′的中点,
∴BE=BC,B′E′=B′C′,
∴BE∶B′E′=BC∶B′C′=k,
∴AD∶A′D′=BE∶B′E′=k.
小结:
两个相似三角形%// //%、
%// //%、
%// //%都等于相似比.
对应高的比
对应角平分线的比
对应中线的比
C
E
A
D
B
C′
E′
A′
D′
B′
例题1图
【例题1】如图,△ABC∽△A′B′C′,AD、BE分别是△ABC的高和中线,A′D′、B′E′分别是△A′B′C′的高和中线,且AD=12,A′D′=9,DE=6.5,求C′D′的长.
解:∵△ABC∽△A′B′C′,∴∠C=∠C′,
又∵AD与A′D′分别是高线,∴△ADC∽△A′D′C′,
∵E与E′分别是AC与A′C′的中点,
由AD=12,A′D′=9,DE=6.5,
∴AC=2DE=13,∴DC=5,
∵AD∶A′D′=DC∶D′C′,
∴D′C′=.
例题2图
C
B
O
A
D
【例题2】如图,小强自制了一个小孔成像装置,其中纸筒的长度为15 cm.他准备了一支长为20 cm的蜡烛,想要得到高度为5 cm的像,蜡烛应放在距离纸筒%// //% cm的地方.
60
1.已知△ABC∽△A′B′C′.若BD和B′D′是它们的对应角平分线,=,B′D′=4,则BD=%// //%.
6
C
E
A
D
B
第2题图
2.如图,在△ABC中AB=5,D,E分别是边AC和AB上的点,且∠ADE=∠B,DE=2,则AD·BC的值为%// //%.
10
y
O
x
C
A
D
B
第3题图
3.如图,点O为坐标原点,点A、B的坐标分别为(9,0)、(6,9),AB延长线一点C的坐标为(5,12),作CD∥BO交x轴于点D,则点D的坐标为%// .
(-3,0)
4.(☆) 如图, 点 在线段 上, 是等边三角形, 且 .
(1) 求 的大小.
(2) 说明线段 之间的数量关系.
解: (1) 是等边三角形,
,
,
,
.
(2) 是等边三角形,
.
,
,
.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
