苏科版数学九年级下册同步课件:6.4第1课时 利用平行证相似(20张ppt)
文档属性
| 名称 | 苏科版数学九年级下册同步课件:6.4第1课时 利用平行证相似(20张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 394.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-14 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
第6章 图形的相似
6.4 第1课时 利用平行证相似
四条线段 a、b、c、d 中,如果 a:b=c:d,那么这四条线段a、b、c、d 叫做成比例的线段,简称比例线段.
2.比例的基本性质
如果 a:b =c:d ,那么ad =bc.
如果 ad =bc,那么 a:b =c:d .
如果 a:b =c:d,那么(a-b):b =(c-d):d;
(a+b):b =(c+d):d.
1.比例线段的概念:
知识回顾
如图,小方格边长都为1,平行线l1 ∥l2∥ l3分别交直线m,n于点 。
获取新知
(1)计算 与
的值,你有什么发现?
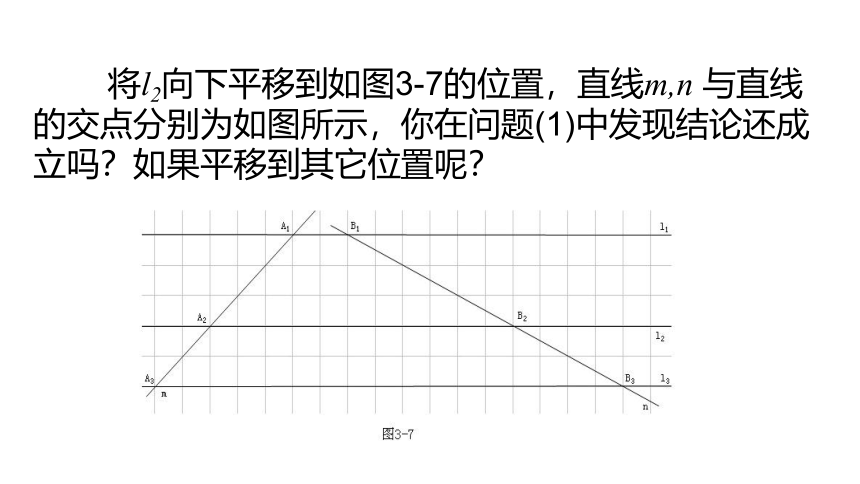
将l2向下平移到如图3-7的位置,直线m,n 与直线的交点分别为如图所示,你在问题(1)中发现结论还成立吗?如果平移到其它位置呢?
猜想:在平面上任意作三条平行线,用它们截两条直线,截得的线段成比例吗?
操作:
(1)请同学在草稿纸上画出三条平行线l1 ∥l2∥ l3.
(2)画出两条截线m,n交三条平行线于
(3)度量 和 的长度,并计算
和 的值,并进行比较.
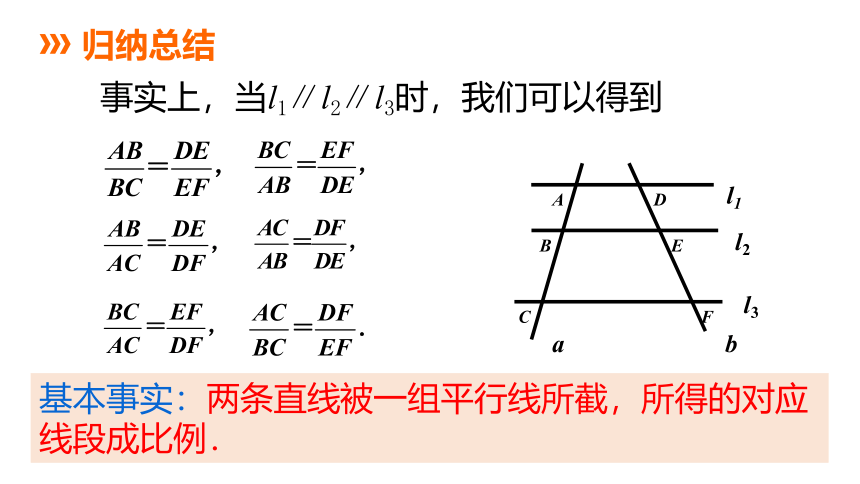
事实上,当l1∥l2∥l3时,我们可以得到
A
B
C
D
E
F
l1
l2
l3
基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
a
b
归纳总结
思考
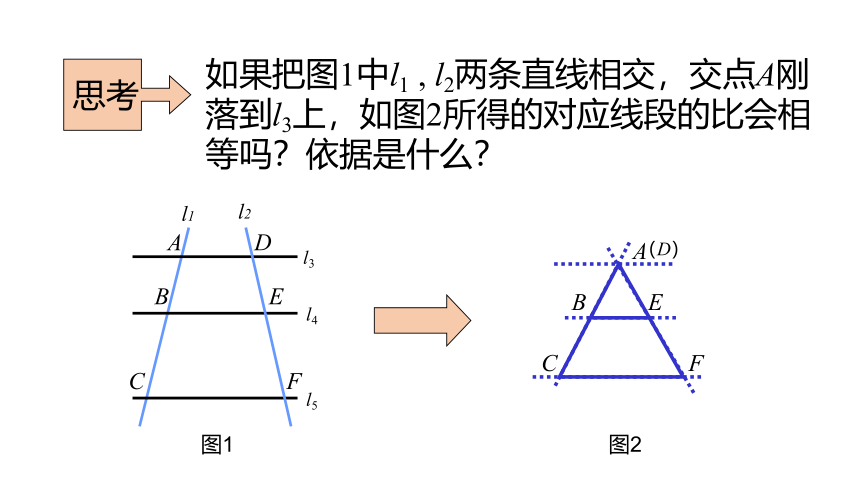
如果把图1中l1 , l2两条直线相交,交点A刚落到l3上,如图2所得的对应线段的比会相等吗?依据是什么?
A
B
C
E
F
图2
A
B
C
D
E
F
l3
l4
l5
l1
l2
(D)
图1
思考
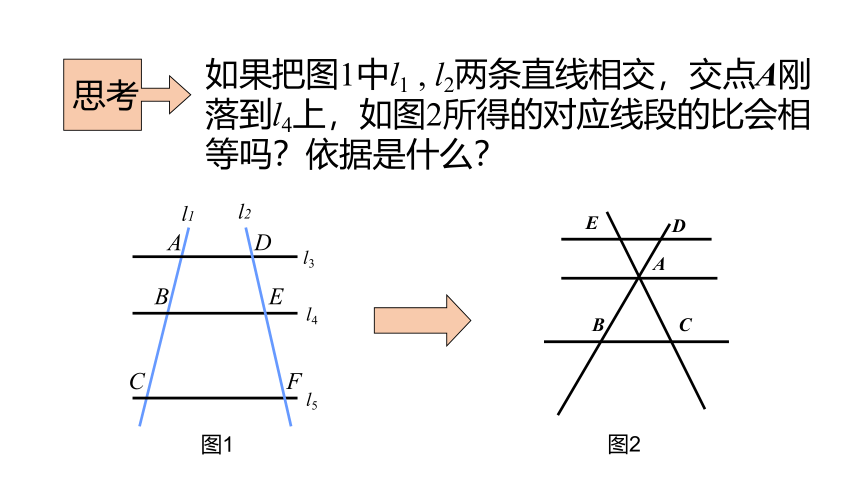
如果把图1中l1 , l2两条直线相交,交点A刚落到l4上,如图2所得的对应线段的比会相等吗?依据是什么?
图2
A
B
C
D
E
F
l3
l4
l5
l1
l2
图1
A
B
C
E
D
l2
l3
l1
l3
l
l
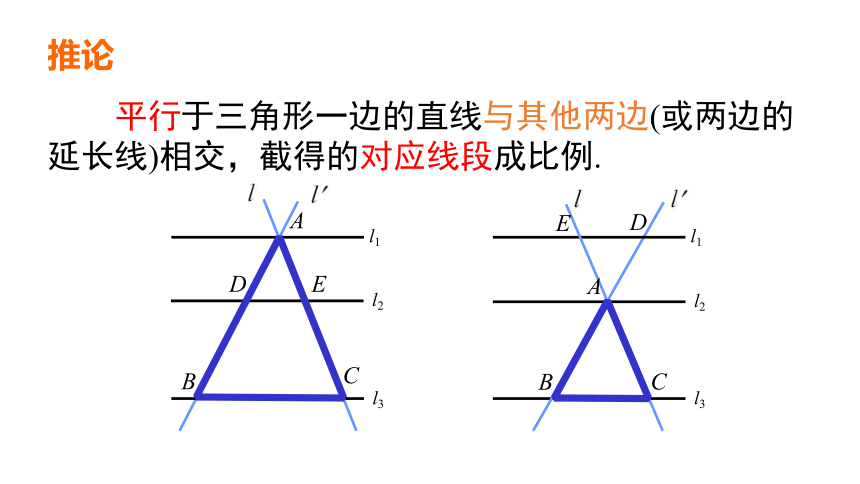
平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的对应线段成比例.
A
B
C
D
E
l2
A
B
C
D
E
l1
l
l
推论
例1 如图,在△ABC 中, 点D、E 分别在AB、AC上,且 DE∥BC,试说明△ADE与△ABC 相似的理由.
D
A
B
C
E
例题讲解
D
A
B
C
E
F
分析:由题意知,在△ADE和△ABC中,各角分别相等,且 ,要说明△ADE∽△ABC,只需要 .为此,把DE平移到FC的位置(作DF∥AC,交BC于点F)就可以了.
解: 过点D作DF∥AC,交BC于点F.
∵DE∥BC,DF∥AC,
∴,,
∵四边形DFCE是平行四边形,
∴DE=FC.
∴.
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C.
∵ ∠DAE=∠BAC,
∴△ADE∽△ABC.
平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的三角形与原三角形相似.
归纳总结
基本模型:
∵DE∥BC
∴△ADE∽△ABC.
∵DE∥BC
∴△ADE∽△ABC.
例2 [教材补充例题] 如图6-4-2,在 ABCD中,点E在CD上, ,BE交对角线AC于点F.则 _______.
C
随堂演练
9
3.如图D-16-3,在△ABC中,点D,E分别在边AB,BC上,
DE∥AC.若BD=4,DA=2,BE=3,则EC= .
图D-16-3
4. 如图,在 □ABCD 中,EF∥AB, DE : EA = 2 : 3,
EF = 4,求 CD 的长.
解:∵ EF∥AB,DE : EA = 2 : 3,
D
A
C
B
E
F
∴ △DEF ∽ △DAB,
∴ 即
解得 AB = 10.
又 ∵ 四边形 ABCD 为平行四边形,
∴ CD = AB = 10.
两条直线被一组平行线所截,所得的对应线段成比例
推论
平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例
相似三角形判定的引理
平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似
基本事实
平行线分线段成比例
课堂小结
第6章 图形的相似
6.4 第1课时 利用平行证相似
四条线段 a、b、c、d 中,如果 a:b=c:d,那么这四条线段a、b、c、d 叫做成比例的线段,简称比例线段.
2.比例的基本性质
如果 a:b =c:d ,那么ad =bc.
如果 ad =bc,那么 a:b =c:d .
如果 a:b =c:d,那么(a-b):b =(c-d):d;
(a+b):b =(c+d):d.
1.比例线段的概念:
知识回顾
如图,小方格边长都为1,平行线l1 ∥l2∥ l3分别交直线m,n于点 。
获取新知
(1)计算 与
的值,你有什么发现?
将l2向下平移到如图3-7的位置,直线m,n 与直线的交点分别为如图所示,你在问题(1)中发现结论还成立吗?如果平移到其它位置呢?
猜想:在平面上任意作三条平行线,用它们截两条直线,截得的线段成比例吗?
操作:
(1)请同学在草稿纸上画出三条平行线l1 ∥l2∥ l3.
(2)画出两条截线m,n交三条平行线于
(3)度量 和 的长度,并计算
和 的值,并进行比较.
事实上,当l1∥l2∥l3时,我们可以得到
A
B
C
D
E
F
l1
l2
l3
基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
a
b
归纳总结
思考
如果把图1中l1 , l2两条直线相交,交点A刚落到l3上,如图2所得的对应线段的比会相等吗?依据是什么?
A
B
C
E
F
图2
A
B
C
D
E
F
l3
l4
l5
l1
l2
(D)
图1
思考
如果把图1中l1 , l2两条直线相交,交点A刚落到l4上,如图2所得的对应线段的比会相等吗?依据是什么?
图2
A
B
C
D
E
F
l3
l4
l5
l1
l2
图1
A
B
C
E
D
l2
l3
l1
l3
l
l
平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的对应线段成比例.
A
B
C
D
E
l2
A
B
C
D
E
l1
l
l
推论
例1 如图,在△ABC 中, 点D、E 分别在AB、AC上,且 DE∥BC,试说明△ADE与△ABC 相似的理由.
D
A
B
C
E
例题讲解
D
A
B
C
E
F
分析:由题意知,在△ADE和△ABC中,各角分别相等,且 ,要说明△ADE∽△ABC,只需要 .为此,把DE平移到FC的位置(作DF∥AC,交BC于点F)就可以了.
解: 过点D作DF∥AC,交BC于点F.
∵DE∥BC,DF∥AC,
∴,,
∵四边形DFCE是平行四边形,
∴DE=FC.
∴.
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C.
∵ ∠DAE=∠BAC,
∴△ADE∽△ABC.
平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的三角形与原三角形相似.
归纳总结
基本模型:
∵DE∥BC
∴△ADE∽△ABC.
∵DE∥BC
∴△ADE∽△ABC.
例2 [教材补充例题] 如图6-4-2,在 ABCD中,点E在CD上, ,BE交对角线AC于点F.则 _______.
C
随堂演练
9
3.如图D-16-3,在△ABC中,点D,E分别在边AB,BC上,
DE∥AC.若BD=4,DA=2,BE=3,则EC= .
图D-16-3
4. 如图,在 □ABCD 中,EF∥AB, DE : EA = 2 : 3,
EF = 4,求 CD 的长.
解:∵ EF∥AB,DE : EA = 2 : 3,
D
A
C
B
E
F
∴ △DEF ∽ △DAB,
∴ 即
解得 AB = 10.
又 ∵ 四边形 ABCD 为平行四边形,
∴ CD = AB = 10.
两条直线被一组平行线所截,所得的对应线段成比例
推论
平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例
相似三角形判定的引理
平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似
基本事实
平行线分线段成比例
课堂小结
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
