苏科版数学九年级下册同步课件:6.4第3课时 利用两边及夹角证相似(共19张PPT)
文档属性
| 名称 | 苏科版数学九年级下册同步课件:6.4第3课时 利用两边及夹角证相似(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 617.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-14 00:00:00 | ||
图片预览


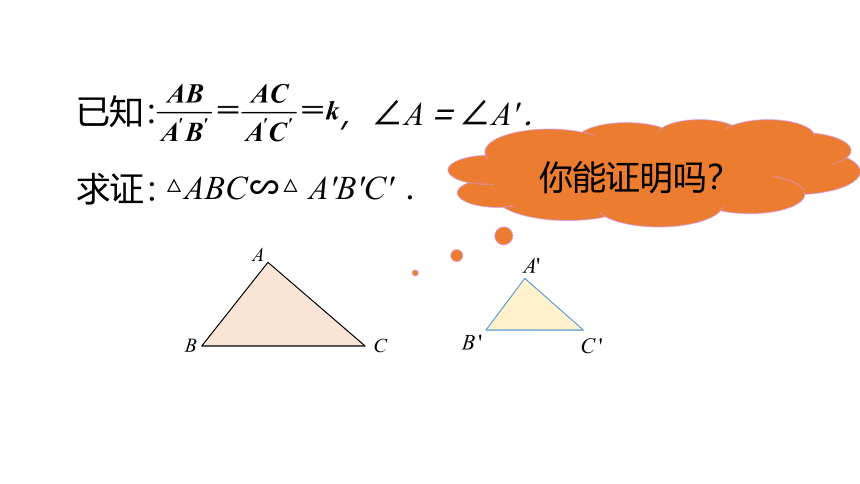

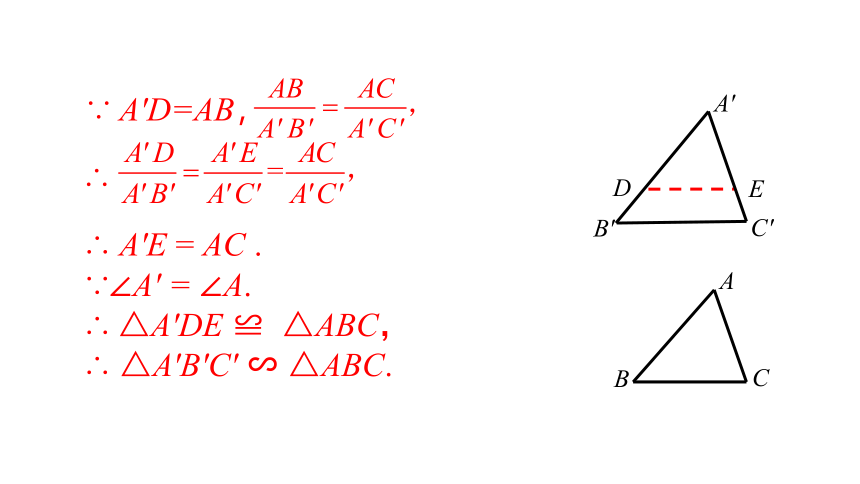

文档简介
(共19张PPT)
第6章 图形的相似
6.4 第3课时 利用两边及夹角证相似
知识回顾
相似三角形的判定依据有哪些?
(1)定义:各角对应相等、各边对应成比例的两个三角形,叫做相似三角形。
(2)两角对应相等的两个三角形相似.
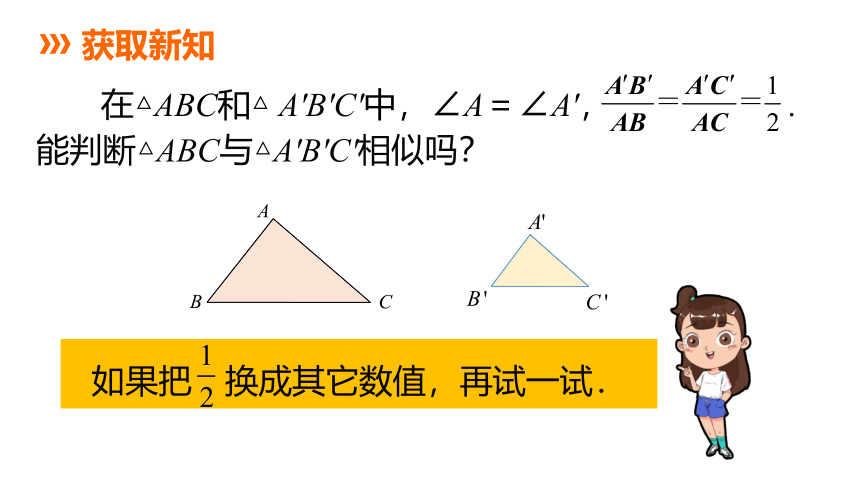
在△ABC和△ A'B'C'中,∠A=∠A', .
能判断△ABC与△A'B'C'相似吗?
如果把 换成其它数值,再试一试.
获取新知
△ABC∽△ A'B'C' .
求证:
已知:
你能证明吗?
,∠A=∠A'.
我们来证明一下前面得出的结论:
如图,在△ABC与△A′B′C′中,已知∠A= ∠A′,
证明:在 △A′B′C′ 的边 A′B′ 上截取点D,使 A′ D = AB.过点 D 作 DE∥B′C′,交 A′C′ 于点 E.
∵ DE∥B′C′,
∴ △A′DE∽△A′B′C′.
求证:△ABC∽△A′B′C′.
B
A
C
D
E
B'
A'
C'
∴
∴ A′E = AC .
∵∠A′ = ∠A.
∴ △A′DE ≌ △ABC,
∴ △A′B′C′ ∽ △ABC.
∵ A′D=AB,
∴
B
A
C
D
E
B'
A'
C'
由此得到利用两边和夹角来判定三角形相似的定理:
两边成比例且夹角相等的两个三角形相似.
符号语言:
∵ ∠A=∠A′,
B
A
C
B'
A'
C'
∴ △ABC ∽ △A′B′C′ .
归纳:
例1 【教材补充例题】如图,已知∠BAC=∠EAD,AB=20.4,AC=48,AE=17,AD=40.
求证:△ABC∽△AED.
解析:已知∠BAC=∠EAD,要判断这两个三角形相似,只要判断 与 相等即可.
例题讲解
提示:解题时要找准对应边.
证明: ∵ CD 是边 AB 上的高,
∴ ∠ADC =∠CDB =90°.
∴△ADC ∽△CDB,∴ ∠ACD =∠B,
∴ ∠ACB =∠ACD +∠BCD =∠B +∠BCD = 90°.
例2 如图,在 △ABC 中,CD 是边 AB 上的高,且 ,求证 ∠ACB=90°.
A
B
C
D
∵
【归纳总结】 利用两边及夹角判定两个三角形相似的“三点注意”.
(1)当两个三角形有公共角或对顶角时常采用这种方法;
(2)角:相等的角必是两组对应边的夹角;
(3)边:夹角的两边要注意对应,即长边与长边对应、短边与短边对应.
例3如图,点D在△ABC内,点E在△ABC外,且∠1=∠2,∠3=∠4.△DBE与△ABC相似吗?为什么?
分析:在△DBE和△ABC中,易知∠DBE=∠ABC.如果 = ,那么这两个三角形就相似.
解: △DBE与△ABC相似.
在△ABD与△CBE中,
∵∠1=∠2,∠3=∠4,
∴△ABD∽△CBE
∴,
又∵∠2=∠1,∴∠DBE=∠ABC.
在△DBE和△ABC中,
∵,∠DBE=∠ABC,
∴△DBE∽△ABC
(两边成比例且夹角相等的两个三角形相似)
A
B
C
如图,在△ABC中,AB=4cm,AC=2cm.
(1)在AB上取一点D,当AD=______时△ACD∽△ABC;
(2)在AC的延长线上取一点E,当CE= 时,
△AEB∽△ABC;此时,BE与DC有怎样的位置关系?为什么?
D
E
思考与探索
1
6
解:BE平行于DC,理由如下:
∵△ACD∽△ABC,∴∠ACD=∠ABC.
∵△AEB∽△ABC,∴∠E=∠ABC ,
∴∠ACD=∠E,∴BE∥DC.
C
答案不唯一,
如∠DAB=∠CAE
随堂演练
3.如图,在△ABC中,AB=8,AC=6,点D在AC上,且AD=2,如果要在AB上找一点E,使△ADE与△ABC相似,
那么AE= .
4.已知:如图,AD=3,AC=6,CE=2.1,AB=7.8,试判断△ADE与△ACB是否相似.
课堂小结
本节课,我们学习了相似的什么判定方法?
两边成比例且夹角相等的两个三角形相似.
符号语言:
∵ ∠A=∠A′,
B
A
C
B'
A'
C'
∴ △ABC ∽ △A′B′C′ .
第6章 图形的相似
6.4 第3课时 利用两边及夹角证相似
知识回顾
相似三角形的判定依据有哪些?
(1)定义:各角对应相等、各边对应成比例的两个三角形,叫做相似三角形。
(2)两角对应相等的两个三角形相似.
在△ABC和△ A'B'C'中,∠A=∠A', .
能判断△ABC与△A'B'C'相似吗?
如果把 换成其它数值,再试一试.
获取新知
△ABC∽△ A'B'C' .
求证:
已知:
你能证明吗?
,∠A=∠A'.
我们来证明一下前面得出的结论:
如图,在△ABC与△A′B′C′中,已知∠A= ∠A′,
证明:在 △A′B′C′ 的边 A′B′ 上截取点D,使 A′ D = AB.过点 D 作 DE∥B′C′,交 A′C′ 于点 E.
∵ DE∥B′C′,
∴ △A′DE∽△A′B′C′.
求证:△ABC∽△A′B′C′.
B
A
C
D
E
B'
A'
C'
∴
∴ A′E = AC .
∵∠A′ = ∠A.
∴ △A′DE ≌ △ABC,
∴ △A′B′C′ ∽ △ABC.
∵ A′D=AB,
∴
B
A
C
D
E
B'
A'
C'
由此得到利用两边和夹角来判定三角形相似的定理:
两边成比例且夹角相等的两个三角形相似.
符号语言:
∵ ∠A=∠A′,
B
A
C
B'
A'
C'
∴ △ABC ∽ △A′B′C′ .
归纳:
例1 【教材补充例题】如图,已知∠BAC=∠EAD,AB=20.4,AC=48,AE=17,AD=40.
求证:△ABC∽△AED.
解析:已知∠BAC=∠EAD,要判断这两个三角形相似,只要判断 与 相等即可.
例题讲解
提示:解题时要找准对应边.
证明: ∵ CD 是边 AB 上的高,
∴ ∠ADC =∠CDB =90°.
∴△ADC ∽△CDB,∴ ∠ACD =∠B,
∴ ∠ACB =∠ACD +∠BCD =∠B +∠BCD = 90°.
例2 如图,在 △ABC 中,CD 是边 AB 上的高,且 ,求证 ∠ACB=90°.
A
B
C
D
∵
【归纳总结】 利用两边及夹角判定两个三角形相似的“三点注意”.
(1)当两个三角形有公共角或对顶角时常采用这种方法;
(2)角:相等的角必是两组对应边的夹角;
(3)边:夹角的两边要注意对应,即长边与长边对应、短边与短边对应.
例3如图,点D在△ABC内,点E在△ABC外,且∠1=∠2,∠3=∠4.△DBE与△ABC相似吗?为什么?
分析:在△DBE和△ABC中,易知∠DBE=∠ABC.如果 = ,那么这两个三角形就相似.
解: △DBE与△ABC相似.
在△ABD与△CBE中,
∵∠1=∠2,∠3=∠4,
∴△ABD∽△CBE
∴,
又∵∠2=∠1,∴∠DBE=∠ABC.
在△DBE和△ABC中,
∵,∠DBE=∠ABC,
∴△DBE∽△ABC
(两边成比例且夹角相等的两个三角形相似)
A
B
C
如图,在△ABC中,AB=4cm,AC=2cm.
(1)在AB上取一点D,当AD=______时△ACD∽△ABC;
(2)在AC的延长线上取一点E,当CE= 时,
△AEB∽△ABC;此时,BE与DC有怎样的位置关系?为什么?
D
E
思考与探索
1
6
解:BE平行于DC,理由如下:
∵△ACD∽△ABC,∴∠ACD=∠ABC.
∵△AEB∽△ABC,∴∠E=∠ABC ,
∴∠ACD=∠E,∴BE∥DC.
C
答案不唯一,
如∠DAB=∠CAE
随堂演练
3.如图,在△ABC中,AB=8,AC=6,点D在AC上,且AD=2,如果要在AB上找一点E,使△ADE与△ABC相似,
那么AE= .
4.已知:如图,AD=3,AC=6,CE=2.1,AB=7.8,试判断△ADE与△ACB是否相似.
课堂小结
本节课,我们学习了相似的什么判定方法?
两边成比例且夹角相等的两个三角形相似.
符号语言:
∵ ∠A=∠A′,
B
A
C
B'
A'
C'
∴ △ABC ∽ △A′B′C′ .
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
