苏科版数学九年级下册同步课件:6.6 图形的位似(共20张PPT)
文档属性
| 名称 | 苏科版数学九年级下册同步课件:6.6 图形的位似(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 437.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-14 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
第6章 图形的相似
6.6 图形的位似
A
B
C
C′
A′
B′
如图,△ABC∽△A'B'C',△ABC与△A'B'C'的相似比是2:3,你还能说出哪些结论呢?
知识回顾
答:△ABC与△A'B'C'的周长比为2:3,面积比为4:9,它们的高、中线、角平分线的比为4:9.
情景导入
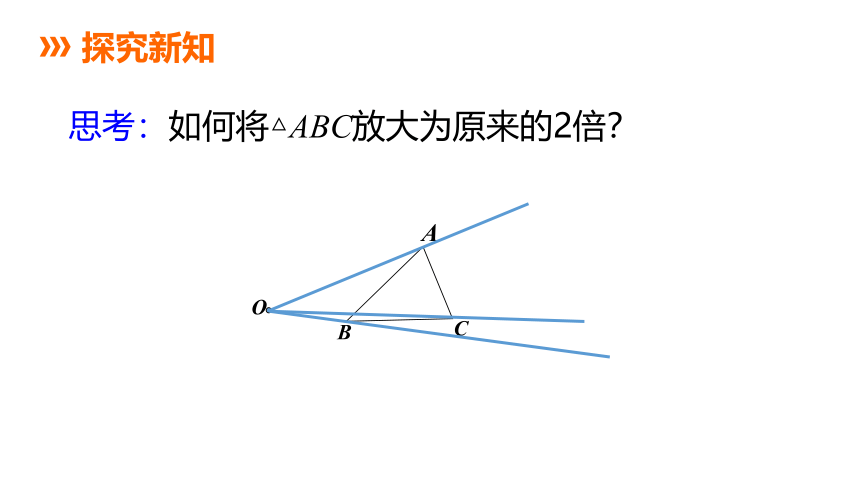
思考:如何将△ABC放大为原来的2倍?
A
C
B
O
探究新知
1.画法:画射线OA、OB、OC,分别在OA、OB、OC上取点A′、B′、C′,使 画△A′B′C′.
2.思考:△ABC与△A′B′C′相似吗
O
A
B
C
C′
B′
A′
如图,已知点O 和△ABC. 将△ABC放大为原来的2倍.
3. 还有其他画法吗?
O
A
B
C
另一种画法:
画法:画射线OA、OB、OC的反向延长线,分别在OA、
OB、OC的反向延长线上取点A′、B′、C′,
使 画△A′B′C′.
O
A
C
B
A′
C′
B′
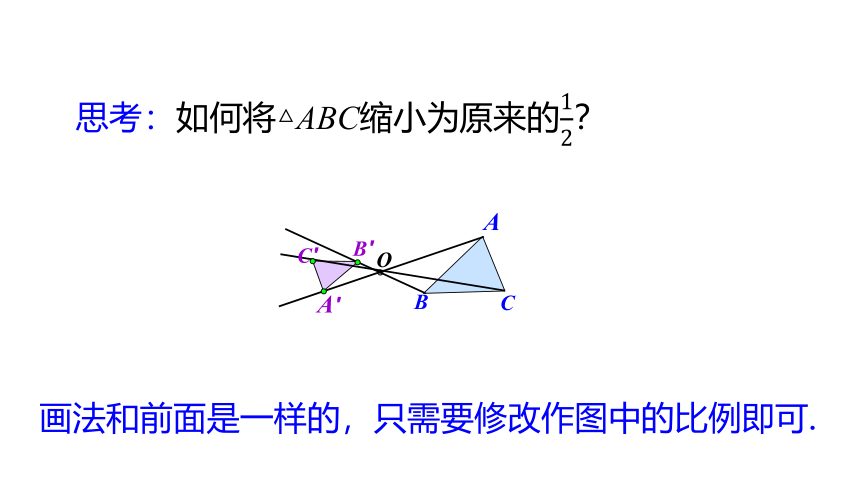
思考:如何将△ABC缩小为原来的?
画法和前面是一样的,只需要修改作图中的比例即可.
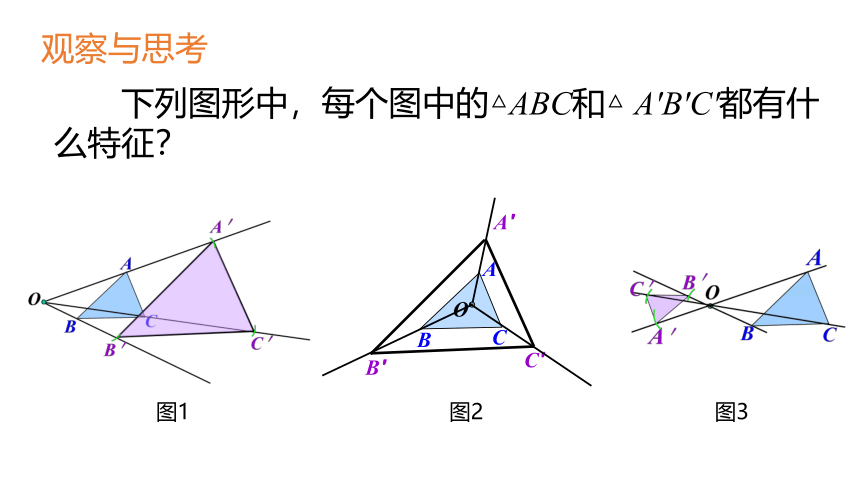
下列图形中,每个图中的△ABC和△ A′B′C′都有什么特征?
A
B
C
C′
B′
A′
O
观察与思考
图1
图2
图3
A
B
A'
C'
B'
C
O
位似形定义:
如果两个多边形不仅相似,而且对应顶点所在直线相交于一点,那么这两个多边形叫做位似形.这个点叫做位似中心.
利用位似可以按所
给相似比把一个图形放
大或缩小.
归纳与总结
观察下面的位似图形,猜想位似图形的性质,并尝试说明理由.
操作与探索
(1)两个位似形一定是相似形;
(2)对应顶点所在的直线都经过同一点;
(3)对应边互相平行(或在同一直线);
(4)任意一组对应点到位似中心的距离之比等于相似比.
位似的性质
归纳与总结
判断:
1.全等图形一定是位似图形. ( )
2.相似图形一定是位似图形. ( )
3.位似图形一定是全等图形. ( )
4.位似图形是具备某种特殊位置的相似图形. ( )
√
×
×
×
试一试
归纳与总结
理解位似概念的“四点注意”
(1)位似图形是一种具有特殊位置关系的相似图形;
(2)位似图形的位似中心只有一个;
(3)位似图形中的两个图形可能位于位似中心的两侧,也可能位于位似中心的一侧;
(4)利用位似图形的定义可以判断两个图形是不是位似图形.
例1 如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0)、A(5,4)、B(3,0),分别将点A,B的横坐标、纵坐标都乘2.得到相应的点A'B'坐标.
(1)画△OA'B'.
(2)△OA'B'与△OAB是位似形吗?
为什么?
例题讲解
解:(1)如图.
(2)△OA'B'与△OAB是位似形.
通过计算可得三边成比例,并且对应点连线都过点O
1.下列图形中△ABC∽△DEF,则这两个三角形不是位似图形的是( )
B
随堂演练
2.如果两个位似图形的相似比为3∶2,那么其面积的比为 .
9∶4
3.如图,△ABC与△DEF是位似三角形,且AC=2DF,则OE∶OB= .
1∶2
5.请在如图D-23-4的正方形网格纸中,以点O为位似中心,将△ABC放大为原来的2倍.(画出一个即可).
图D-23-4
解:如图所示:(答案不唯一,只要作出一个即可)
第6章 图形的相似
6.6 图形的位似
A
B
C
C′
A′
B′
如图,△ABC∽△A'B'C',△ABC与△A'B'C'的相似比是2:3,你还能说出哪些结论呢?
知识回顾
答:△ABC与△A'B'C'的周长比为2:3,面积比为4:9,它们的高、中线、角平分线的比为4:9.
情景导入
思考:如何将△ABC放大为原来的2倍?
A
C
B
O
探究新知
1.画法:画射线OA、OB、OC,分别在OA、OB、OC上取点A′、B′、C′,使 画△A′B′C′.
2.思考:△ABC与△A′B′C′相似吗
O
A
B
C
C′
B′
A′
如图,已知点O 和△ABC. 将△ABC放大为原来的2倍.
3. 还有其他画法吗?
O
A
B
C
另一种画法:
画法:画射线OA、OB、OC的反向延长线,分别在OA、
OB、OC的反向延长线上取点A′、B′、C′,
使 画△A′B′C′.
O
A
C
B
A′
C′
B′
思考:如何将△ABC缩小为原来的?
画法和前面是一样的,只需要修改作图中的比例即可.
下列图形中,每个图中的△ABC和△ A′B′C′都有什么特征?
A
B
C
C′
B′
A′
O
观察与思考
图1
图2
图3
A
B
A'
C'
B'
C
O
位似形定义:
如果两个多边形不仅相似,而且对应顶点所在直线相交于一点,那么这两个多边形叫做位似形.这个点叫做位似中心.
利用位似可以按所
给相似比把一个图形放
大或缩小.
归纳与总结
观察下面的位似图形,猜想位似图形的性质,并尝试说明理由.
操作与探索
(1)两个位似形一定是相似形;
(2)对应顶点所在的直线都经过同一点;
(3)对应边互相平行(或在同一直线);
(4)任意一组对应点到位似中心的距离之比等于相似比.
位似的性质
归纳与总结
判断:
1.全等图形一定是位似图形. ( )
2.相似图形一定是位似图形. ( )
3.位似图形一定是全等图形. ( )
4.位似图形是具备某种特殊位置的相似图形. ( )
√
×
×
×
试一试
归纳与总结
理解位似概念的“四点注意”
(1)位似图形是一种具有特殊位置关系的相似图形;
(2)位似图形的位似中心只有一个;
(3)位似图形中的两个图形可能位于位似中心的两侧,也可能位于位似中心的一侧;
(4)利用位似图形的定义可以判断两个图形是不是位似图形.
例1 如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0)、A(5,4)、B(3,0),分别将点A,B的横坐标、纵坐标都乘2.得到相应的点A'B'坐标.
(1)画△OA'B'.
(2)△OA'B'与△OAB是位似形吗?
为什么?
例题讲解
解:(1)如图.
(2)△OA'B'与△OAB是位似形.
通过计算可得三边成比例,并且对应点连线都过点O
1.下列图形中△ABC∽△DEF,则这两个三角形不是位似图形的是( )
B
随堂演练
2.如果两个位似图形的相似比为3∶2,那么其面积的比为 .
9∶4
3.如图,△ABC与△DEF是位似三角形,且AC=2DF,则OE∶OB= .
1∶2
5.请在如图D-23-4的正方形网格纸中,以点O为位似中心,将△ABC放大为原来的2倍.(画出一个即可).
图D-23-4
解:如图所示:(答案不唯一,只要作出一个即可)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
