苏科版数学九年级下册同步课件:7.1正切(共22张PPT)
文档属性
| 名称 | 苏科版数学九年级下册同步课件:7.1正切(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-14 16:20:02 | ||
图片预览





文档简介
(共22张PPT)
第7章 锐角三角函数
7.1 正切
情景导入
越高越陡峭?
活动1
图中哪个台阶更陡?
相同宽度下台阶的高度越高,台阶越陡;反之,越平坦.
相同高度下台阶的宽度越小,台阶越陡;反之,越平坦.
获取新知
活动2
图中哪个台阶最陡?
乙>甲
甲
丙
乙
乙>丙
台阶乙最陡.
方法总结:同高比宽,同宽比高.
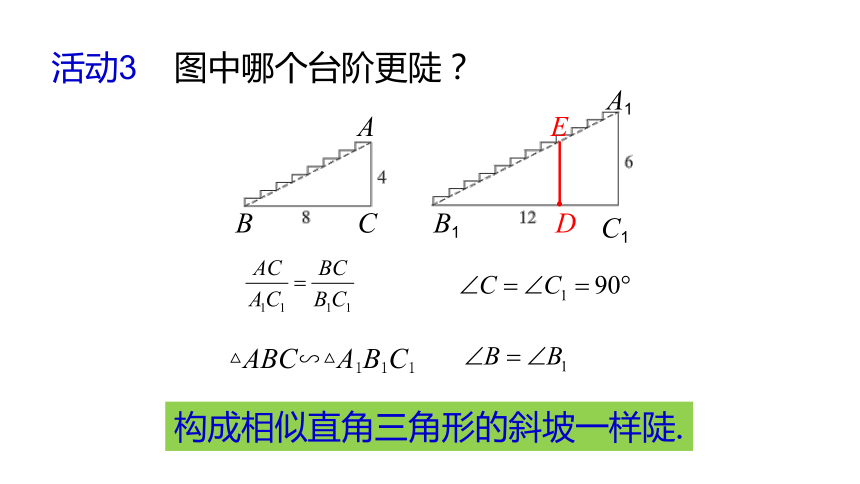
活动3
图中哪个台阶更陡?
A
C
B
C1
A1
B1
△ABC∽△A1B1C1
D
E
构成相似直角三角形的斜坡一样陡.
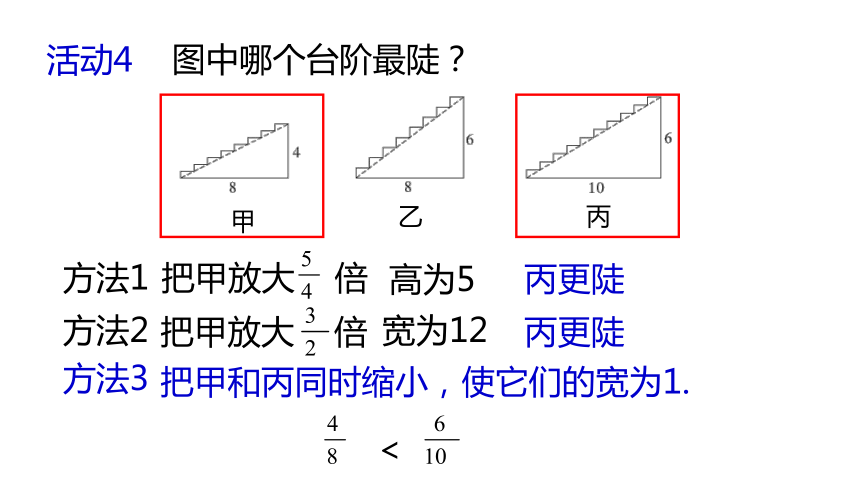
活动4
图中哪个台阶最陡?
甲
丙
乙
方法1
把甲放大 倍
高为5
丙更陡
方法2
把甲放大 倍
宽为12
丙更陡
方法3
把甲和丙同时缩小,使它们的宽为1.
<
A
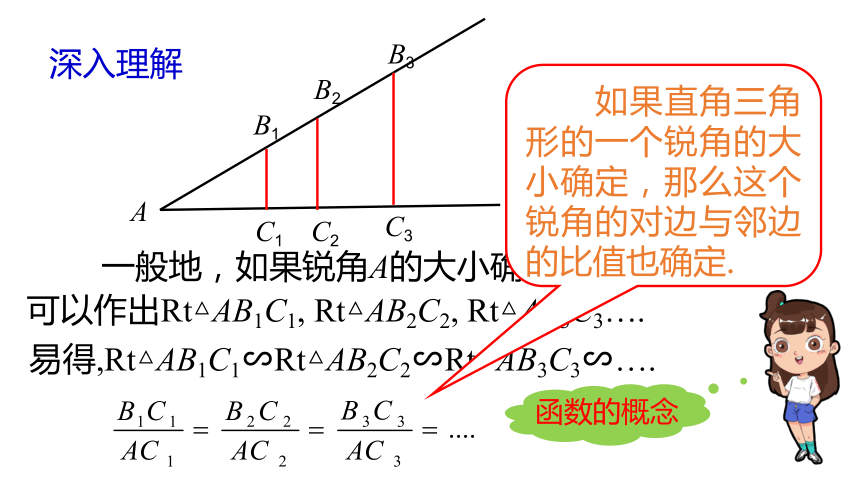
一般地,如果锐角A的大小确定,我们
可以作出Rt△AB1C1, Rt△AB2C2, Rt△AB3C3….
C1
B1
C2
B2
B3
C3
易得,Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3∽….
如果直角三角形的一个锐角的大小确定,那么这个锐角的对边与邻边的比值也确定.
函数的概念
深入理解
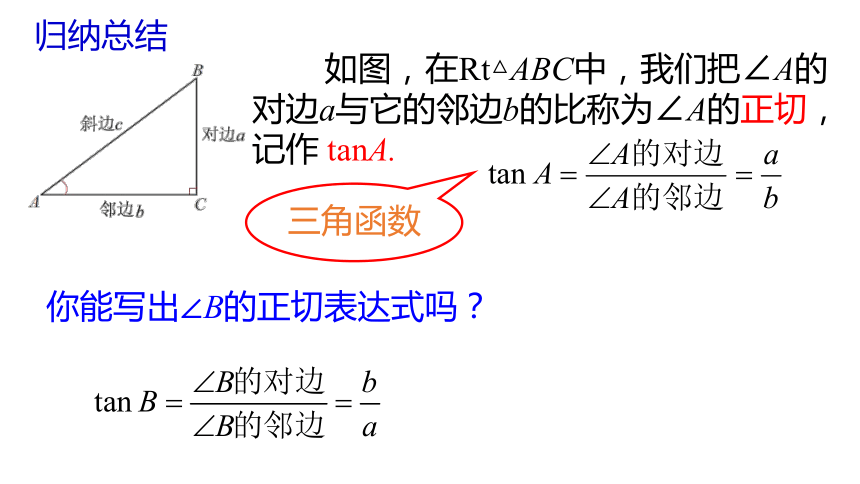
如图,在Rt△ABC中,我们把∠A的对边a与它的邻边b的比称为∠A的正切,记作 tanA.
归纳总结
三角函数
你能写出∠B的正切表达式吗?
1.tanA是一个完整的符号,它表示∠A的正切,记号里习惯省去角的符号“∠”;
2.tanA没有单位,它表示一个比值,即直角三角形中∠A的对边与邻边的比;
3.tanA不表示“tan”乘以“A”.
注意:
例1 如图,在Rt△ABC中,∠C=90°,AC=4,AB=5.求tanA.
例题讲解
解:在Rt△ABC中,根据勾股定理,得
BC== =3
∴tanA== .
利用正切的概念进行计算的“两种类型”
(1)在直角三角形中,已知两直角边,直接使用正切的概念计算;
(2)在直角三角形中,已知一条直角边和斜边,先根据勾股定理求出另一条直角边,再使用正切的概念计算.
归纳总结
B
C
A
1
牛刀小试:根据下列图中所给条件分别求出下列图中∠A、∠B的正切值.
A
2
C
1
B
B
A
C
3
5
通过上述计算,你有什么发现?
互余两角的正切值互为倒数.
tanA=,tanB=
tanA=,tanB=
tanA=,tanB=
例2 如图,在等边三角形ABC中,CD⊥AB,垂足为D.求tanA.
解:由题意知,AD= AB= AC.
在Rt△ADC中,根据勾股定理,得
CD== ·AD=
∴tanA==.
例3 如图,在Rt△ABC中,∠C=90°,AC=3,tanA=2,求AB的值.
B
A
C
解:∵ tanA=2 ,∴ =2,
∵ AC=3 ∴BC=6,
∴在Rt△AB中AB2=BC2+AC2,
∴AB2=32+62 ,
∴AB= 3 .
自变量和函数分别是什么?
自变量的取值范围是什么?
0°<∠A < 90°
∠A
tanA
归纳总结
怎样计算任意一个锐角的正切值呢?
你能计算一个65°角的正切的近似值吗
1
获取新知
如图,我们可以这样来确定tan65°的近似值:当一个点从O出发沿着65°线移动到点P时,这个点沿水平方向前进了一个单位长度,沿竖直方向上升了约2.14个单位.于是可知tan65°≈ 2.14 .
θ tanθ
10°
20°
30°
45°
55°
65° 2.14
思考:当锐角θ越来越大时,θ的正切值有什么变化?
结论:锐角θ的正切值随锐角θ的增大而增大.
0.18
0.36
0.58
1
1.43
0
1
tanθ > 0
随堂检测
如图,在Rt△ABC中,∠C=90°,则tanB= (填结果).
2.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.
(1)tanA==;
(2)tanB==.
3.比较大小:tan21° tan31°.
4.如图,在△ABC中,∠C=90°,AC=2,BC=1,则tanA的值是 .
5.如图,点A(t,4)在第一象限,OA与x轴所夹的锐角为α,tanα=,则t的值是 .
一个方法:
一个结论:
用定义求正切值.
锐角θ的正切值随锐角θ的增大而增大.
一个定义:
在Rt△ABC中,∠C=90°,∠A的对边a与邻边b的比叫做∠A的正切,记作tanA=
课堂小结
第7章 锐角三角函数
7.1 正切
情景导入
越高越陡峭?
活动1
图中哪个台阶更陡?
相同宽度下台阶的高度越高,台阶越陡;反之,越平坦.
相同高度下台阶的宽度越小,台阶越陡;反之,越平坦.
获取新知
活动2
图中哪个台阶最陡?
乙>甲
甲
丙
乙
乙>丙
台阶乙最陡.
方法总结:同高比宽,同宽比高.
活动3
图中哪个台阶更陡?
A
C
B
C1
A1
B1
△ABC∽△A1B1C1
D
E
构成相似直角三角形的斜坡一样陡.
活动4
图中哪个台阶最陡?
甲
丙
乙
方法1
把甲放大 倍
高为5
丙更陡
方法2
把甲放大 倍
宽为12
丙更陡
方法3
把甲和丙同时缩小,使它们的宽为1.
<
A
一般地,如果锐角A的大小确定,我们
可以作出Rt△AB1C1, Rt△AB2C2, Rt△AB3C3….
C1
B1
C2
B2
B3
C3
易得,Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3∽….
如果直角三角形的一个锐角的大小确定,那么这个锐角的对边与邻边的比值也确定.
函数的概念
深入理解
如图,在Rt△ABC中,我们把∠A的对边a与它的邻边b的比称为∠A的正切,记作 tanA.
归纳总结
三角函数
你能写出∠B的正切表达式吗?
1.tanA是一个完整的符号,它表示∠A的正切,记号里习惯省去角的符号“∠”;
2.tanA没有单位,它表示一个比值,即直角三角形中∠A的对边与邻边的比;
3.tanA不表示“tan”乘以“A”.
注意:
例1 如图,在Rt△ABC中,∠C=90°,AC=4,AB=5.求tanA.
例题讲解
解:在Rt△ABC中,根据勾股定理,得
BC== =3
∴tanA== .
利用正切的概念进行计算的“两种类型”
(1)在直角三角形中,已知两直角边,直接使用正切的概念计算;
(2)在直角三角形中,已知一条直角边和斜边,先根据勾股定理求出另一条直角边,再使用正切的概念计算.
归纳总结
B
C
A
1
牛刀小试:根据下列图中所给条件分别求出下列图中∠A、∠B的正切值.
A
2
C
1
B
B
A
C
3
5
通过上述计算,你有什么发现?
互余两角的正切值互为倒数.
tanA=,tanB=
tanA=,tanB=
tanA=,tanB=
例2 如图,在等边三角形ABC中,CD⊥AB,垂足为D.求tanA.
解:由题意知,AD= AB= AC.
在Rt△ADC中,根据勾股定理,得
CD== ·AD=
∴tanA==.
例3 如图,在Rt△ABC中,∠C=90°,AC=3,tanA=2,求AB的值.
B
A
C
解:∵ tanA=2 ,∴ =2,
∵ AC=3 ∴BC=6,
∴在Rt△AB中AB2=BC2+AC2,
∴AB2=32+62 ,
∴AB= 3 .
自变量和函数分别是什么?
自变量的取值范围是什么?
0°<∠A < 90°
∠A
tanA
归纳总结
怎样计算任意一个锐角的正切值呢?
你能计算一个65°角的正切的近似值吗
1
获取新知
如图,我们可以这样来确定tan65°的近似值:当一个点从O出发沿着65°线移动到点P时,这个点沿水平方向前进了一个单位长度,沿竖直方向上升了约2.14个单位.于是可知tan65°≈ 2.14 .
θ tanθ
10°
20°
30°
45°
55°
65° 2.14
思考:当锐角θ越来越大时,θ的正切值有什么变化?
结论:锐角θ的正切值随锐角θ的增大而增大.
0.18
0.36
0.58
1
1.43
0
1
tanθ > 0
随堂检测
如图,在Rt△ABC中,∠C=90°,则tanB= (填结果).
2.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.
(1)tanA==;
(2)tanB==.
3.比较大小:tan21° tan31°.
4.如图,在△ABC中,∠C=90°,AC=2,BC=1,则tanA的值是 .
5.如图,点A(t,4)在第一象限,OA与x轴所夹的锐角为α,tanα=,则t的值是 .
一个方法:
一个结论:
用定义求正切值.
锐角θ的正切值随锐角θ的增大而增大.
一个定义:
在Rt△ABC中,∠C=90°,∠A的对边a与邻边b的比叫做∠A的正切,记作tanA=
课堂小结
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
