苏科版数学九年级下册同步课件:7.5 第1课时 解直角三角形(共14张PPT)
文档属性
| 名称 | 苏科版数学九年级下册同步课件:7.5 第1课时 解直角三角形(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 283.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-14 00:00:00 | ||
图片预览




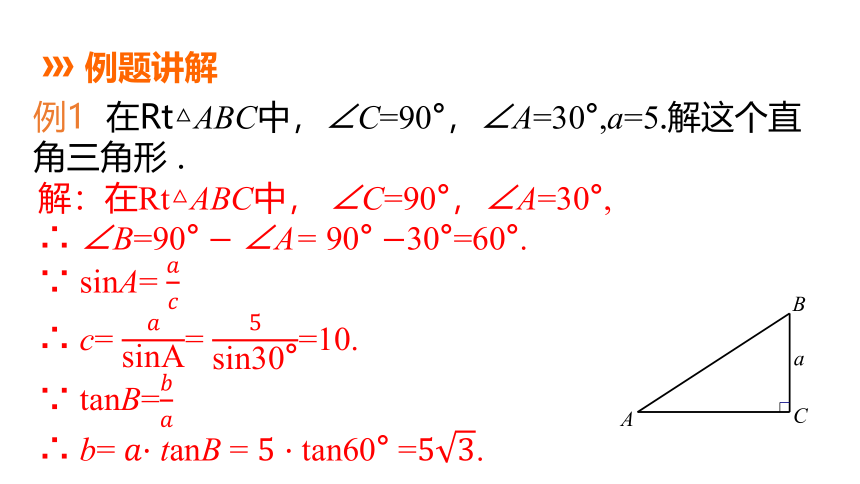


文档简介
(共14张PPT)
第7章 锐角三角函数
7.5 第1课时 解直角三角形
在直角三角形中,除直角外,还有哪些元素
这5个元素之间有什么关系
知识回顾
a
C
B
A
c
b
②锐角之间关系:
③边角之间关系:
①三边之间关系:
在直角三角形中:
∠A+∠B=90°.
a2+b2=c2(勾股定理).
a
C
B
A
c
b
利用边、角关系,如果知道其中的2个元素(其中至少有一个是边),那么就可以求出其余的3个未知元素.
由直角三角形中的已知元素,求出所有未知元素的过程,叫做解直角三角形.
获取新知
a
C
B
A
c
b
例1 在Rt△ABC中,∠C=90°,∠A=30°,a=5.解这个直角三角形 .
例题讲解
a
C
B
A
解:在Rt△ABC中, ∠C=90°,∠A=30°,
∴ ∠B=90° ∠A= 90° 30°=60°.
∵ sinA=
∴ c= = =10.
∵ tanB=
∴ b= tanB = tan60° =.
例2 已知:在Rt△ABC中,∠C=90°,a=104,b= 20.49.
求: (1)c的值(精确到0.01);
(2)∠A、∠B的大小(精确到0.01°).
a
C
B
A
b
解:(1)在Rt△ABC中,根据勾股定理,得
c== ,
用计算器计算,得c≈106.00.
(2)由题意知,tanA== ,
用计算器计算,得∠A≈78.85°
∴∠B =90° 78.85°=11.15°.
1.在Rt△ABC中,∠C=90°,如果AB=6,cosA=,那么AC= .
随堂演练
2.如图,已知△ABC,过点A作BC边的垂线,交BC于点D,若BC=5,AD=4,tan∠BAD=,则DC= .
4
2
[解析] 由题意得AD⊥BC,即∠ADB=∠ADC=90°.
在Rt△ABD中,AD=4, tan∠BAD==,
∴BD=3,
∴CD=BC-BD=5-3=2.
3.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,AC=8,BC=6,则∠ACD的正切值是 .
[解析]在Rt△ABC中,∵∠ACB=90°,CD是AB边上的中线,
∴CD=AD,
∴∠A=∠ACD.
∵∠ACB=90°,BC=6,AC=8,
∴tanA===,
∴tan∠ACD= tanA=,即∠ACD的正切值为.
4.在Rt△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C所对的边,请根据下列条件解直角三角形:
(1)a=10,∠A=45°;
(2)a=5,b=5;
(3)a=2,c=7(角度精确到1').
解:(1)∠B=45°,b=10,c=10.
(2)∠A=30°,∠B=60°,c=10.
(3)∠A≈44°25',∠B≈45°35',b=5.
解直角三角形的概念
(勾股定理)
三边之间关系
边角之间关系
(锐角三角函数)
简单
应用
两锐角之间关系
课堂小结
第7章 锐角三角函数
7.5 第1课时 解直角三角形
在直角三角形中,除直角外,还有哪些元素
这5个元素之间有什么关系
知识回顾
a
C
B
A
c
b
②锐角之间关系:
③边角之间关系:
①三边之间关系:
在直角三角形中:
∠A+∠B=90°.
a2+b2=c2(勾股定理).
a
C
B
A
c
b
利用边、角关系,如果知道其中的2个元素(其中至少有一个是边),那么就可以求出其余的3个未知元素.
由直角三角形中的已知元素,求出所有未知元素的过程,叫做解直角三角形.
获取新知
a
C
B
A
c
b
例1 在Rt△ABC中,∠C=90°,∠A=30°,a=5.解这个直角三角形 .
例题讲解
a
C
B
A
解:在Rt△ABC中, ∠C=90°,∠A=30°,
∴ ∠B=90° ∠A= 90° 30°=60°.
∵ sinA=
∴ c= = =10.
∵ tanB=
∴ b= tanB = tan60° =.
例2 已知:在Rt△ABC中,∠C=90°,a=104,b= 20.49.
求: (1)c的值(精确到0.01);
(2)∠A、∠B的大小(精确到0.01°).
a
C
B
A
b
解:(1)在Rt△ABC中,根据勾股定理,得
c== ,
用计算器计算,得c≈106.00.
(2)由题意知,tanA== ,
用计算器计算,得∠A≈78.85°
∴∠B =90° 78.85°=11.15°.
1.在Rt△ABC中,∠C=90°,如果AB=6,cosA=,那么AC= .
随堂演练
2.如图,已知△ABC,过点A作BC边的垂线,交BC于点D,若BC=5,AD=4,tan∠BAD=,则DC= .
4
2
[解析] 由题意得AD⊥BC,即∠ADB=∠ADC=90°.
在Rt△ABD中,AD=4, tan∠BAD==,
∴BD=3,
∴CD=BC-BD=5-3=2.
3.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,AC=8,BC=6,则∠ACD的正切值是 .
[解析]在Rt△ABC中,∵∠ACB=90°,CD是AB边上的中线,
∴CD=AD,
∴∠A=∠ACD.
∵∠ACB=90°,BC=6,AC=8,
∴tanA===,
∴tan∠ACD= tanA=,即∠ACD的正切值为.
4.在Rt△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C所对的边,请根据下列条件解直角三角形:
(1)a=10,∠A=45°;
(2)a=5,b=5;
(3)a=2,c=7(角度精确到1').
解:(1)∠B=45°,b=10,c=10.
(2)∠A=30°,∠B=60°,c=10.
(3)∠A≈44°25',∠B≈45°35',b=5.
解直角三角形的概念
(勾股定理)
三边之间关系
边角之间关系
(锐角三角函数)
简单
应用
两锐角之间关系
课堂小结
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
