苏科版数学九年级下册同步课件:7.6 第3课时 与仰角、俯角和方向角有关的问题(共16张PPT)
文档属性
| 名称 | 苏科版数学九年级下册同步课件:7.6 第3课时 与仰角、俯角和方向角有关的问题(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 365.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-14 00:00:00 | ||
图片预览


文档简介
(共16张PPT)
第7章 锐角三角函数
7.6 第3课时
与仰角、俯角和方向角有关的问题
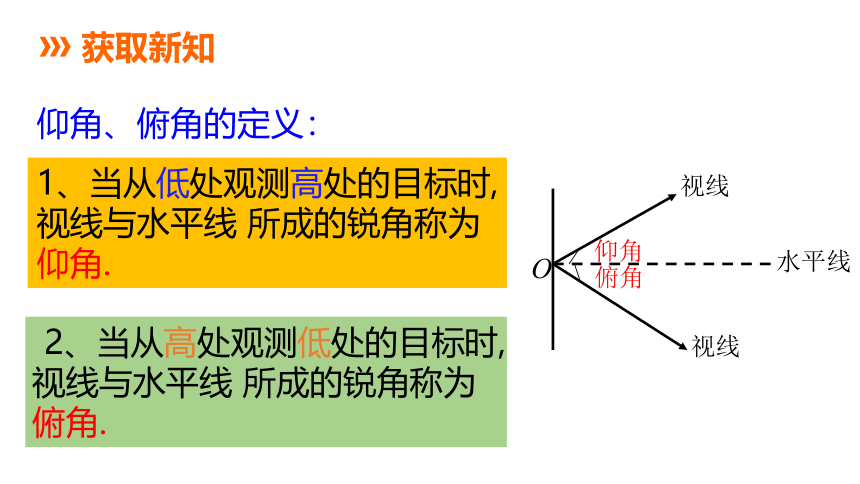
仰角
俯角
视线
视线
水平线
O
2、当从高处观测低处的目标时,视线与水平线 所成的锐角称为俯角.
1、当从低处观测高处的目标时,视线与水平线 所成的锐角称为仰角.
获取新知
仰角、俯角的定义:
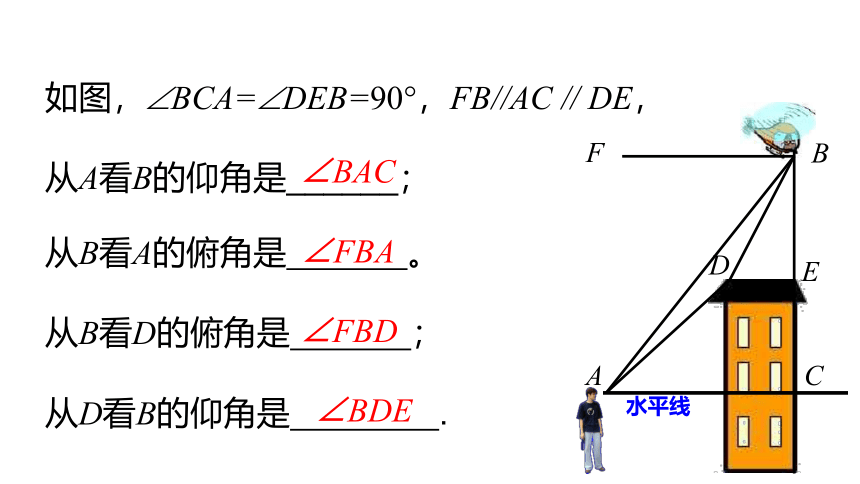
如图, BCA= DEB=90 ,FB//AC // DE,
从A看B的仰角是______;
从B看A的俯角是 。
从B看D的俯角是 ;
从D看B的仰角是 .
D
A
C
E
B
F
∠FBD
∠BDE
∠FBA
∠BAC
水平线
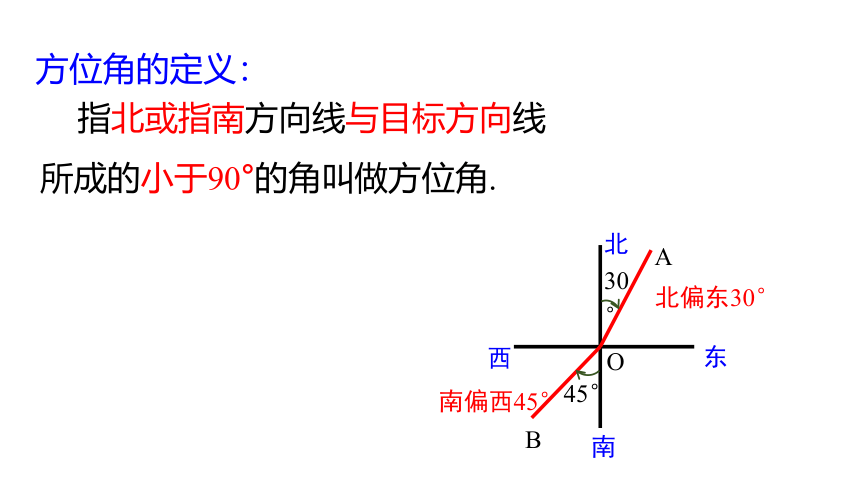
方位角的定义:
指北或指南方向线与目标方向线所成的小于90°的角叫做方位角.
30°
45°
B
O
A
东
西
北
南
北偏东30°
南偏西45°
东
西
北
O
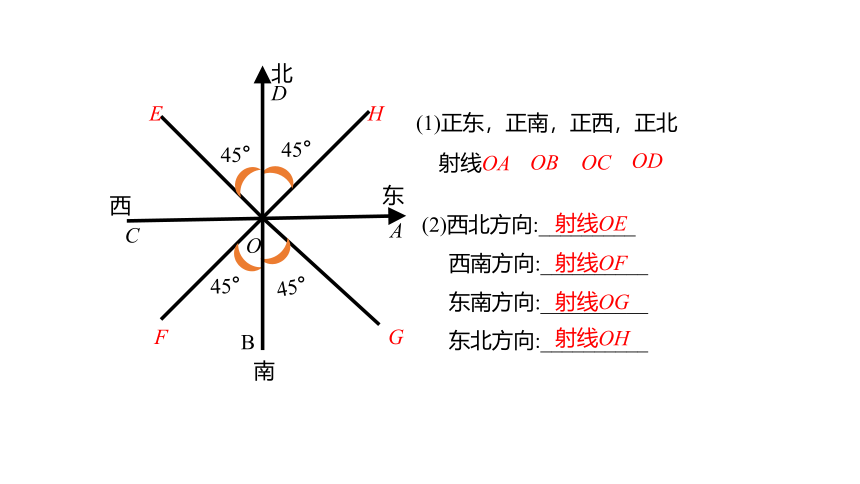
(1)正东,正南,正西,正北
(2)西北方向:_________
西南方向:__________
东南方向:__________
东北方向:__________
射线OA
A
B
C
D
OB
OC
45°
射线OE
射线OF
射线OG
射线OH
E
G
F
H
45°
45°
45°
南
OD
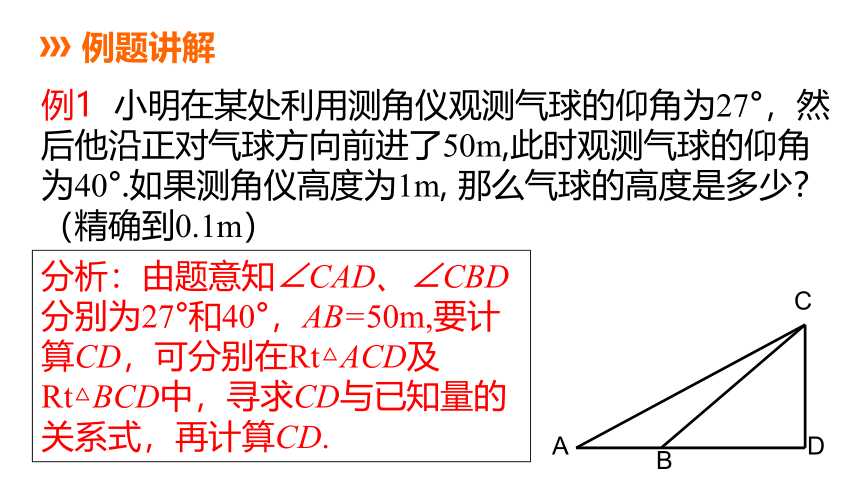
例1 小明在某处利用测角仪观测气球的仰角为27°,然后他沿正对气球方向前进了50m,此时观测气球的仰角为40°.如果测角仪高度为1m, 那么气球的高度是多少?(精确到0.1m)
A
D
B
C
例题讲解
分析:由题意知∠CAD、∠CBD分别为27°和40°,AB=50m,要计算CD,可分别在Rt△ACD及Rt△BCD中,寻求CD与已知量的关系式,再计算CD.
解:如图,点A、B、C分别表示小明两次观测点及气球位置.由题意知,∠CAD=27°,∠CBD=40°,CD⊥AD,AB=50m,设CD=x m.
在Rt△BDC中,由tan40°= ,得BD= .
在Rt△ADC中,由tan27°= ,得AD= .
∵AD BD=50,
∴ ∴ = .
用计算器计算, 64.9.
A
D
B
C
例2 如图,已知在港口A得南偏东75°方向有一礁石B,轮船从港口出发,沿东北方向(北偏东45°方向)前行10千米到达C后测得礁石B在其南偏西15°处,求轮船行驶过程中离礁石B的最近距离.
解:由题意易得∠BAC=45°+90°-75°=60°,
∠ACB=45°-15°=30°,
∴∠ABC=90°,∴AB=AC=5千米.
如图,过点B作BD⊥AC于点D,则在Rt△ABD中,
BD=AB·sin60°=5×=(千米),
∴轮船行驶过程中离礁石B的最近距离为千米.
解决方向角问题的“三点注意”
(1)方向角一般是以第一个方向为始边向另一个方向旋转相应度数.
(2)在解决有关方向角的问题时,一般要根据题意理清图形中各角系,有时所给的方向角并不一定在直角三角形中,需要用两直线平行,内错角相等,或等角的余角相等等知识转化为所需要的角.
(3)一般以“上北下南,左西右东”确定方向角.
归纳总结
1.在山顶A处观测山脚B处的俯角为36°,则在B处观测A处的仰角为 °.
2.如图,小明在操场上距离旗杆18米的C处,用测角仪测得旗杆AB的顶端A的仰角为30°,已知
测角仪CD的高为1.4米,那么旗杆AB的
高为 米.
36
随堂演练
3.如图,我市在凤城河风景区举办了端午节赛龙舟活动,小亮在河畔的一幢楼上看到一艘龙舟迎面驶来,他在高出水面15 m的A处测得在C处的龙舟俯角为23°;他登高6 m到正上方的B处测得驶至D处的龙舟俯角为50°,则两次观测期间龙舟前进了多少米
(结果精确到1 m,参考数据:
tan23°≈0.42,tan40°≈0.84,tan50°≈1.19,tan67°≈2.36)
解:如图,根据题意,得∠C=23°,∠BDE=50°,AE=15 m,BE=AE+AB=21 m.
在Rt△ACE中,
tanC=tan23°==≈0.42,解得CE≈35.7(m).
在Rt△BDE中,
tan∠BDE=tan50°==≈1.19,解得DE≈17.6(m).
∴CD=CE-DE≈35.7-17.6=18.1≈18(m).
答:两次观测期间龙舟前进了约18 m.
4.钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和渔政部门对钓鱼岛海域实现了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A,B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留根号)
解:作BD⊥AC于点D,
由题意可知,∠BAC=45°,∠ABC=105°,
∴∠ACB=180°-∠BAC-∠ABC=30°,
在Rt△ABD中,
BD=AB·sin∠BAD=20× =10 (海里),
在Rt△BCD中,BC= = =20 (海里),
答:此时船C与船B的距离是20 海里.
课堂小结
如何利用锐角三角函数解决与仰角、俯角和方向角有关的问题
(1)根据题意抽象出数学图形.
(2)能构造出与求解相关的直角三角形.
第7章 锐角三角函数
7.6 第3课时
与仰角、俯角和方向角有关的问题
仰角
俯角
视线
视线
水平线
O
2、当从高处观测低处的目标时,视线与水平线 所成的锐角称为俯角.
1、当从低处观测高处的目标时,视线与水平线 所成的锐角称为仰角.
获取新知
仰角、俯角的定义:
如图, BCA= DEB=90 ,FB//AC // DE,
从A看B的仰角是______;
从B看A的俯角是 。
从B看D的俯角是 ;
从D看B的仰角是 .
D
A
C
E
B
F
∠FBD
∠BDE
∠FBA
∠BAC
水平线
方位角的定义:
指北或指南方向线与目标方向线所成的小于90°的角叫做方位角.
30°
45°
B
O
A
东
西
北
南
北偏东30°
南偏西45°
东
西
北
O
(1)正东,正南,正西,正北
(2)西北方向:_________
西南方向:__________
东南方向:__________
东北方向:__________
射线OA
A
B
C
D
OB
OC
45°
射线OE
射线OF
射线OG
射线OH
E
G
F
H
45°
45°
45°
南
OD
例1 小明在某处利用测角仪观测气球的仰角为27°,然后他沿正对气球方向前进了50m,此时观测气球的仰角为40°.如果测角仪高度为1m, 那么气球的高度是多少?(精确到0.1m)
A
D
B
C
例题讲解
分析:由题意知∠CAD、∠CBD分别为27°和40°,AB=50m,要计算CD,可分别在Rt△ACD及Rt△BCD中,寻求CD与已知量的关系式,再计算CD.
解:如图,点A、B、C分别表示小明两次观测点及气球位置.由题意知,∠CAD=27°,∠CBD=40°,CD⊥AD,AB=50m,设CD=x m.
在Rt△BDC中,由tan40°= ,得BD= .
在Rt△ADC中,由tan27°= ,得AD= .
∵AD BD=50,
∴ ∴ = .
用计算器计算, 64.9.
A
D
B
C
例2 如图,已知在港口A得南偏东75°方向有一礁石B,轮船从港口出发,沿东北方向(北偏东45°方向)前行10千米到达C后测得礁石B在其南偏西15°处,求轮船行驶过程中离礁石B的最近距离.
解:由题意易得∠BAC=45°+90°-75°=60°,
∠ACB=45°-15°=30°,
∴∠ABC=90°,∴AB=AC=5千米.
如图,过点B作BD⊥AC于点D,则在Rt△ABD中,
BD=AB·sin60°=5×=(千米),
∴轮船行驶过程中离礁石B的最近距离为千米.
解决方向角问题的“三点注意”
(1)方向角一般是以第一个方向为始边向另一个方向旋转相应度数.
(2)在解决有关方向角的问题时,一般要根据题意理清图形中各角系,有时所给的方向角并不一定在直角三角形中,需要用两直线平行,内错角相等,或等角的余角相等等知识转化为所需要的角.
(3)一般以“上北下南,左西右东”确定方向角.
归纳总结
1.在山顶A处观测山脚B处的俯角为36°,则在B处观测A处的仰角为 °.
2.如图,小明在操场上距离旗杆18米的C处,用测角仪测得旗杆AB的顶端A的仰角为30°,已知
测角仪CD的高为1.4米,那么旗杆AB的
高为 米.
36
随堂演练
3.如图,我市在凤城河风景区举办了端午节赛龙舟活动,小亮在河畔的一幢楼上看到一艘龙舟迎面驶来,他在高出水面15 m的A处测得在C处的龙舟俯角为23°;他登高6 m到正上方的B处测得驶至D处的龙舟俯角为50°,则两次观测期间龙舟前进了多少米
(结果精确到1 m,参考数据:
tan23°≈0.42,tan40°≈0.84,tan50°≈1.19,tan67°≈2.36)
解:如图,根据题意,得∠C=23°,∠BDE=50°,AE=15 m,BE=AE+AB=21 m.
在Rt△ACE中,
tanC=tan23°==≈0.42,解得CE≈35.7(m).
在Rt△BDE中,
tan∠BDE=tan50°==≈1.19,解得DE≈17.6(m).
∴CD=CE-DE≈35.7-17.6=18.1≈18(m).
答:两次观测期间龙舟前进了约18 m.
4.钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和渔政部门对钓鱼岛海域实现了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A,B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留根号)
解:作BD⊥AC于点D,
由题意可知,∠BAC=45°,∠ABC=105°,
∴∠ACB=180°-∠BAC-∠ABC=30°,
在Rt△ABD中,
BD=AB·sin∠BAD=20× =10 (海里),
在Rt△BCD中,BC= = =20 (海里),
答:此时船C与船B的距离是20 海里.
课堂小结
如何利用锐角三角函数解决与仰角、俯角和方向角有关的问题
(1)根据题意抽象出数学图形.
(2)能构造出与求解相关的直角三角形.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
