15.2全等三角形判定(一)课件
图片预览





文档简介
课件16张PPT。全等三角形判定一株木中学:聂光英复习:1.全等三角形的定义
2.全等三角形的性质能完全重合的两个三角形,
叫做全等三角形。全等三角形的对应边相等,
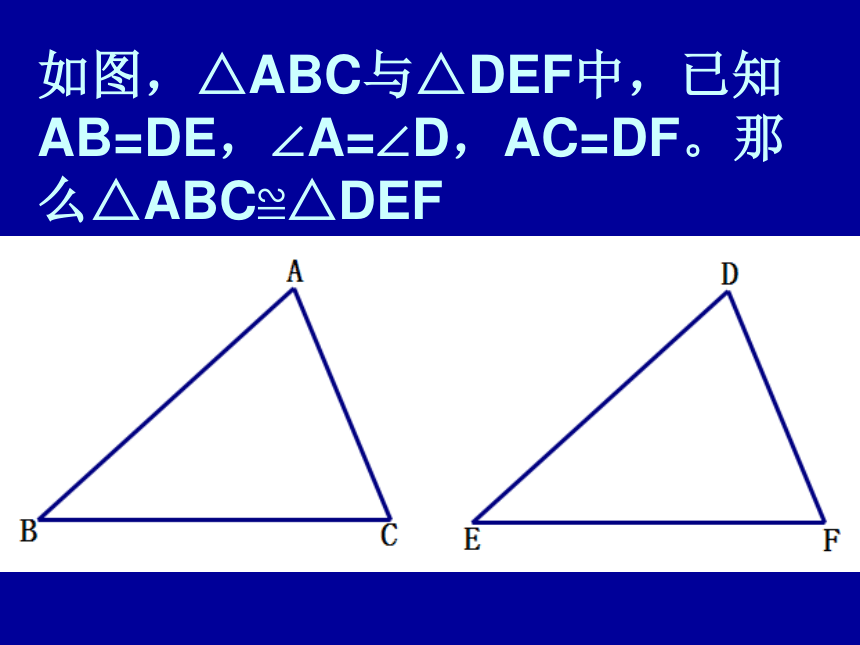
对应角相等。如图,△ABC与△DEF中,已知AB=DE,∠A=∠D,AC=DF。那么△ABC≌△DEF全等三角形判定方法1.在两个三角形中,如果有两条边及它们的夹角对应相等,
那么这两个三角形全等
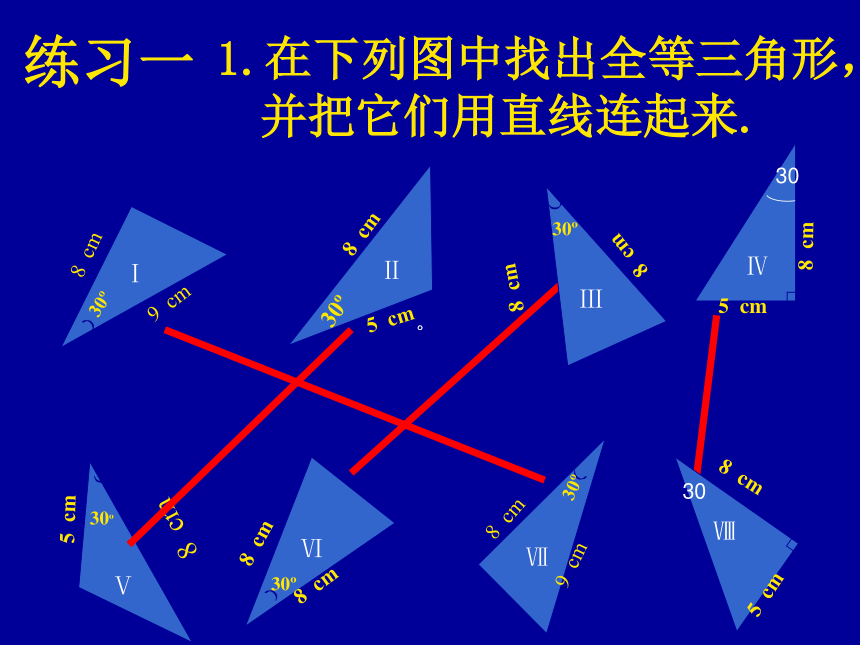
(简记为S.A.S)1.在下列图中找出全等三角形,并把它们用直线连起来.Ⅳ练习一。。例题1.如图,BD与CE相交于A,已知AB=AD,AC=AE,求证△ BAC≌△ DAE。证明:在△ BAC与△ DAE中,AB=AD(已知)∠BAC=∠DAE(对顶角相等)AC=AE(已知)∴△ BAC≌△ DAE(SAS)注意:证明的每一步都要有根据,这些根据可以是已知条件,也可以是学过的定义、公理和定理。例题2.如图,已知AB=AD,AC=AE,∠BAD=∠CAE, 说明△BAC与△DAE全等的理由。
解:在△ BAC与△ DAE中,AB=AD(已知)∠BAD=∠CAE(已知)AC=AE(已知)∴△ BAC≌△ DAE(SAS)BAC 即:∠BAC+∠CAD=∠CAD+∠DAE A∴ ∠BAC=∠DAE (等式的性质)AD=EAD+CAD∠BAC=∠DAE(已证)例题3:如图,已知AB=CD,∠ABC=∠DCB,那么△ABC与△DCB是否全等?为什么?解:△ ABC≌△ DCBAB=DC(已知)∠ABC=∠DCB(已知)BC=CB(公共边)∴△ ABC≌△ DCB(SAS)在△ ABC与△ DCB中,小结通过今天的学习你会用SAS来证明两个三角形全等了吗?怎样证说说你的思路。根据题中的已知条件和学过的定义、定理、公理找出这两个三角形中的相等边和相等角,一定是两条边及它们的夹角对应相等。AE=AD已知如图,AB=AC,若按“SAS”判定方法证明△ABD≌△ACE,则还应补充条件是________________或______________。BE=CD练一练已知如图,AB∥DE,AB=DE,BE=CF 说明(3)AC∥DF(1)BC=EF(2)△ABC≌△DEF解(1) BE=CF(已知) BE+CE=CF+CE(等式的性质) 即 BC=EF(2) AB∥DE(已知) ∠B=∠DEF (两直线平行同位角相等)
在△ABC与△DEF中有:
AB=DE(已知)
∠B=∠DEF (已证)
BC=EF(已证)
△ABC≌△DEF (SAS) (3) △ABC≌△DEF (已证) ∠ACB= ∠F (全等三角形对应角相等)
AC∥DF (同位角相等两直线平行)
谢谢指导!
2.全等三角形的性质能完全重合的两个三角形,
叫做全等三角形。全等三角形的对应边相等,
对应角相等。如图,△ABC与△DEF中,已知AB=DE,∠A=∠D,AC=DF。那么△ABC≌△DEF全等三角形判定方法1.在两个三角形中,如果有两条边及它们的夹角对应相等,
那么这两个三角形全等
(简记为S.A.S)1.在下列图中找出全等三角形,并把它们用直线连起来.Ⅳ练习一。。例题1.如图,BD与CE相交于A,已知AB=AD,AC=AE,求证△ BAC≌△ DAE。证明:在△ BAC与△ DAE中,AB=AD(已知)∠BAC=∠DAE(对顶角相等)AC=AE(已知)∴△ BAC≌△ DAE(SAS)注意:证明的每一步都要有根据,这些根据可以是已知条件,也可以是学过的定义、公理和定理。例题2.如图,已知AB=AD,AC=AE,∠BAD=∠CAE, 说明△BAC与△DAE全等的理由。
解:在△ BAC与△ DAE中,AB=AD(已知)∠BAD=∠CAE(已知)AC=AE(已知)∴△ BAC≌△ DAE(SAS)BAC 即:∠BAC+∠CAD=∠CAD+∠DAE A∴ ∠BAC=∠DAE (等式的性质)AD=EAD+CAD∠BAC=∠DAE(已证)例题3:如图,已知AB=CD,∠ABC=∠DCB,那么△ABC与△DCB是否全等?为什么?解:△ ABC≌△ DCBAB=DC(已知)∠ABC=∠DCB(已知)BC=CB(公共边)∴△ ABC≌△ DCB(SAS)在△ ABC与△ DCB中,小结通过今天的学习你会用SAS来证明两个三角形全等了吗?怎样证说说你的思路。根据题中的已知条件和学过的定义、定理、公理找出这两个三角形中的相等边和相等角,一定是两条边及它们的夹角对应相等。AE=AD已知如图,AB=AC,若按“SAS”判定方法证明△ABD≌△ACE,则还应补充条件是________________或______________。BE=CD练一练已知如图,AB∥DE,AB=DE,BE=CF 说明(3)AC∥DF(1)BC=EF(2)△ABC≌△DEF解(1) BE=CF(已知) BE+CE=CF+CE(等式的性质) 即 BC=EF(2) AB∥DE(已知) ∠B=∠DEF (两直线平行同位角相等)
在△ABC与△DEF中有:
AB=DE(已知)
∠B=∠DEF (已证)
BC=EF(已证)
△ABC≌△DEF (SAS) (3) △ABC≌△DEF (已证) ∠ACB= ∠F (全等三角形对应角相等)
AC∥DF (同位角相等两直线平行)
谢谢指导!
