第七章 平行线的证明单元测试卷(较易)(含解析)
文档属性
| 名称 | 第七章 平行线的证明单元测试卷(较易)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 170.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-14 16:15:06 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
北师大版初中数学八年级上册第七单元《平行线的证明》单元测试卷
考试范围:第七章; 考试时间:100分钟;总分120分,
学校:___________姓名:___________班级:___________考号:___________
注意:本试卷包含Ⅰ、Ⅱ两卷。第Ⅰ卷为选择题,所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题,所有答案必须填在答题卷的相应位置。答案写在试卷上均无效,不予记分。
第I卷(选择题)
一、选择题(本大题共12小题,共36分)
下列关于判断一个数学结论是否正确的叙述,正确的是
A. 只需观察得出 B. 只需依靠经验获得
C. 通过亲自试验得出 D. 必须进行有根据的证实
根据一周天可以制作出每年的“星期几密码”现已知年的“星期几密码”是“”,这组密码中从左到右的个数字依次与年的到月对应,我们可以用这组密码算出年某天是星期几.如年月日,其中月对应密码中的第二个数字“”,将数字加上日期,其和为,再把除以,得余数,则该天为星期四余数几则对应星期几,特别地,余数则对应星期天.
利用此密码算出年的世界环境日月日是
A. 星期一 B. 星期二 C. 星期四 D. 星期六
小英、小亮、小明和小华四名同学参加了“大梦杯”竞赛选拔赛,小亮和小华两个同学的得分和等于小明和小英的得分和;小英与小亮的得分和大于小明和小华的得分和;小华的得分超过小明与小亮的得分和.则这四位同学的得分由大到小的顺序是
A. 小明、小亮、小华、小英 B. 小华、小明、小亮、小英
C. 小英、小华、小亮、小明 D. 小亮、小英、小华、小明
以下四个命题:如果一个数的相反数等于它本身,则这个数是一个数的倒数等于它本身,则这个数是一个数的算术平方根等于它本身,则这个数是或如果一个数的绝对值等于它本身,则这个数是正数其中真命题有
A. 个 B. 个 C. 个 D. 个
将命题“对顶角相等”写成“如果那么”的形式,正确的是
如果两个角相等,那么它们是对顶角
如果两个角是对顶角,那么它们相等
C. 如果对顶角,那么相等
D. 如果两个角不是对顶角,那么这两个角不相等
如图,不能判定的是
A. B.
C. D.
一次数学活动中,检验两条纸带、的边线是否平行,小明和小丽采用两种不同的方法:如图,小明对纸带沿折叠,量得小丽对纸带沿折叠,发现与重合,与重合则下列判断正确的是
A. 纸带的边线平行,纸带的边线不平行
B. 纸带的边线不平行,纸带的边线平行
C. 纸带的边线都平行
D. 纸带的边线都不平行
将一块直角三角板按如图方式放置,其中,,两点分别落在直线、上,,添加下列哪一个条件可使直线
A.
B.
C.
D.
如图,下列推理及所证明的理由都正确的是
A. 若,则,理由是内错角相等,两直线平行
B. 若,则,理由是两直线平行,内错角相等
C. 若,则,理由是内错角相等,两直线平行
D. 若,则,理由是两直线平行,内错角相等
如图,,,,,的面积为,则四边形的面积为
A.
B.
C.
D.
下列判断:
三角形的三个内角中最多有一个钝角;
三角形的三个内角中至少有两个锐角;
有两个内角为和的三角形一定是钝角三角形;
直角三角形中两锐角的和为.
其中判断正确的有 .
A. 个 B. 个 C. 个 D. 个
将一把直尺和一块含和角的三角板按如图所示的位置放置,如果,那么的大小为
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
如图, .
如图,点在的延长线上,对于给出的四个条件:
;
;
;
.
能判断的有______填写序号.
命题“如果,那么,互为相反数”的逆命题为______.
天干地支纪年法是上古文明的产物,又称节气历或中国阳历有十天干与十二地支,如下表:
天干 甲 乙 丙 丁 戊 己 庚 辛 壬 癸
地支 子 丑 寅 卯 辰 巳 午 未 申 酉 戌 亥
算法如下:先用年份的尾数查出天干,再用年份除以的余数查出地支如年,尾数为戊,除以余数为,为子,那么年就是戊子年.
年是伟大、光荣、正确的中国共产党成立周年,则年是______ 年用天干地支纪年法表示
三、解答题(本大题共8小题,共72分)
有五个足球队、、、、分入同一小组进行单循环足球比赛,争夺出线权,比赛规定:胜一场得分,平一场得分,负一场得分,小组中名次在前的两个队出线,小组赛结束后,如果队的积分为分,讨论:
队的战绩是几胜,几平,几负?
如果小组赛中有一个队的战绩为全胜,队能否出线?
如果小组赛中有一个队的积分为,队能否出线?
写出下列命题的逆命题,这些逆命题都成立吗?
两直线平行,同位角相等;
如果实数,那么;
直角都相等.
如图,在平行四边形中,对角线与交于点,且,请你从,,平分中任选一个作为添加条件,另两个中的一个作为结论,组成一个真命题,并证明.
添加条件:______,结论:______;填序号
根据你所选择的条件和结论,写出证明过程.
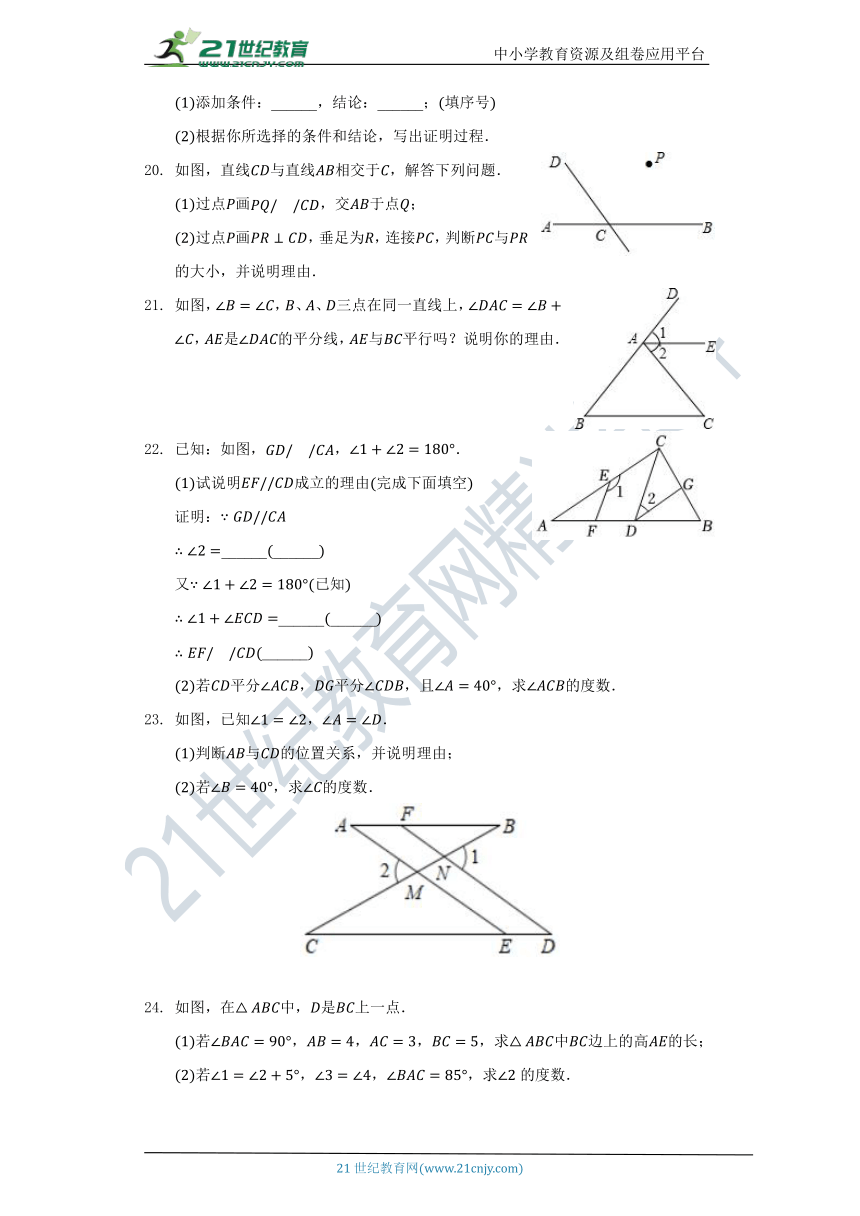
如图,直线与直线相交于,解答下列问题.
过点画,交于点;
过点画,垂足为,连接,判断与的大小,并说明理由.
如图,,、、三点在同一直线上,,是的平分线,与平行吗?说明你的理由.
已知:如图,,.
试说明成立的理由完成下面填空
证明:
____________
又已知
____________
______
若平分,平分,且,求的度数.
如图,已知,.
判断与的位置关系,并说明理由;
若,求的度数.
如图,在中,是上一点.
若,,,,求中边上的高的长;
若,,,求的度数.
答案和解析
1.【答案】
【解析】
【分析】
本题考查了数学结论是怎样得到的,必须有严密的逻辑证明过程.要判断一个数学结论是否正确,仅仅依靠经验,观察或实验是不够的,必须每一步都要有根有据地进行推理.
【解答】
解:经验,观察或实验只能为数学活动提供思路,要想得到正确结论,每一步都要有严密的逻辑推理过程,
故选: .
2.【答案】
【解析】
【分析】
本题考查了推理与论证,关键是理解题意.根据题意得出 月对应第六个数字 ,将数字 加上日期 ,和为 ,用 除以 求出商和余数,再根据余数即可求解.
【解答】
解:依题意得: 月对应第六个数字 ,
将数字 加上日期 ,和为 ,
,
故 年的世界环境日 月 日 是星期二.
故选: .
3.【答案】
【解析】
【分析】
本题主要考查了推理与论证的问题,能够通过已知条件找出突破口,从而通过推理得出结论.
由题干中前两个条件可得小英的得分大于小华的,小亮的大于小明的,再结合第三个条件,进而可出结论.
【解答】
解:由题干中小亮和小华两个同学的得分和等于小明和小英的得分和;
小英与小亮的得分和大于小明和小华的得分和,
可得小英的得分大于小华的,小亮的大于小明的;
又有小华的得分超过小明与小亮的得分和,
所以可得四位同学的得分由大到小的顺序是小英、小华、小亮、小明.
4.【答案】
【解析】
【分析】
本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果 那么 ”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.
根据相反数的定义对 进行判断;根据 的倒数等于 可对 进行判断;根据算术平方根的定义对 进行判断;根据 的绝对值等于 可对 进行判断.
【解答】
解:如果一个数的相反数等于它本身,则这个数是 ,所以 正确;
一个数的倒数等于它本身,则这个数是 或 ,所以 错误;
一个数的算术平方根等于它本身,则这个数是 或 ,所以 正确;
如果一个数的绝对值等于它本身,则这个数是正数或 ,所以 错误.
故选 B .
5.【答案】
【解析】
【分析】
本题考查命题与定理,先把原命题分成题设和结论,然后变成如果 那么 的形式即可,注意改写过程语句要通顺.
【解答】
解:对顶角相等写成“如果 那么 ”的形式为:如果两个角是对顶角,那么它们相等;
故选 B .
6.【答案】
【解析】
【分析】
本题考查平行线的判定,解题的关键是熟练掌握基本知识,属于中考常考题型.
利用平行线的判定方法一一判断即可.
【解答】
解: 由 ,根据同位角相等两直线平行,即可判断 .
B. 由 ,根据内错角相等两直线平行,即可判断 .
C. 由 ,根据同旁内角互补两直线平行,即可判断 .
D. 由 不能判定 .
故选: .
7.【答案】
【解析】
【分析】
此题主要考查了平行线的判定以及翻折变换的性质,正确掌握翻折变换的性质是解题关键.直接利用翻折变换的性质结合平行线的判定方法得出答案.
【解析】
解:如图 所示,因为 , ,
所以 ,
所以 ,
所以 ,所以纸带 的边线不平行.
如图所示,因为与重合,与重合,
所以,,
所以,同旁内角互补,两直线平行
所以纸带的边线平行.
故选B.
8.【答案】
【解析】
【分析】
本题考查了平行线的判定,熟练掌握平行线的判定定理是解题关键 利用平行线的判定定理:内错角相等,两直线平行即可解答.
【解答】
解:因为 构成的角与 是内错角,
所以要使直线 ,只需 ,
又因为 , ,
所以可添加的条件是 .
故选 D .
9.【答案】
【解析】
【分析】
本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.根据平行线的性质,进行判断即可.
【解答】
解: 若 ,则 ,理由是两直线平行,内错角相等,故选项 A 错误;
B. 若 ,则 ,并不是 ,理由是两直线平行,内错角相等,故选项 B 错误;
C. 若 ,则 ,理由是两直线平行,内错角相等,故选项 C 错误;
D. 若 ,则 ,理由是两直线平行,内错角相等,正确;
故选: .
10.【答案】
【解析】解:,,
四边形为平行四边形,
,
,
,
点和点到的距离相等,
设点到的距离为,
的面积为,
,
解得,
四边形的面积.
故选:.
先判断四边形为平行四边形得到,则,再利用得到点和点到的距离相等,设点到的距离为,利用的面积为可计算出,然后根据平行四边形的面积公式计算四边形的面积.
本题考查了三角形的面积:三角形的面积等于底边长与高线乘积的一半,即底高.也考查了平行线的性质.
11.【答案】
【解析】
【分析】
此题考查了三角形的内角和定理.解题时要仔细分析,理解题意.因为三角形的内角和为 ,所以三角形的三个内角中最多有一个钝角,三角形的三个内角中至少有两个锐角,据此可对 作出判断;有两个内角为 和 的三角形的第三角为 ,所以一定是钝角三角形,据此可对 作出判断;因为直角三角形中有一个角等于 ,所以直角三角形中两锐角的和为 ,据此可对 作出判断.
【解答】
解:因为三角形的内角和为 ,所以三角形的三个内角中最多有一个钝角,三角形的三个内角中至少有两个锐角,所以 是正确的;
有两个内角为 和 的三角形的第三角为 ,所以一定是钝角三角形,所以 正确;
因为直角三角形中有一个角等于 ,所以直角三角形中两锐角的和为 ,所以 正确.
可得 都正确,
故选 D .
12.【答案】
【解析】
【分析】
本题主要考查平行线的性质,解题的关键是掌握两直线平行同位角相等与三角形外角的性质.
由 得 ,再根据三角形的外角性质可得答案.
【解答】
解:由题意知 ,
,
,
.
13.【答案】
【解析】略
14.【答案】
【解析】解:根据内错角相等,两直线平行即可证得;
根据内错角相等,两直线平行即可证得,不能证明;
根据同位角相等,两直线平行即可证得;
根据同旁内角互补,两直线平行即可证得,不能证明.
故答案为:.
根据平行线的判定定理进行逐一判断即可.
本题考查了平行线的判定定理,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
15.【答案】如果,互为相反数,那么
【解析】
【分析】
本题考查的是命题与定理、互逆命题,掌握逆命题的确定方法是解题的关键.
根据互逆命题的定义写出逆命题即可.
【解答】
解:命题“如果 ,那么 , 互为相反数”的逆命题为:
如果 , 互为相反数,那么 ;
故答案为:如果 , 互为相反数,那么 .
16.【答案】辛丑
【解析】解:年,尾数为辛,除以余数为,为丑,那么年就是辛丑年.
故答案为:辛丑.
先用的尾数查出天干,再用除以的余数查出地支即可.
本题是考查了推理,读懂天干地支的算法是解决本题的关键.
17.【答案】解:个队进行单循环足球比赛,
每个队间只比赛次,每个队和其他队比赛次,
设队胜,平,
,
得:,,故A队的战绩是胜平负.
小组赛中有一个队的战绩为全胜,队的积分为分,
其他队最多可以胜场比赛,故最多可得分,
队能出线;
假设是队的战绩为分.它就是胜平败.
可以看出,队只败给了队.就是说,,,都败给队了.
队里有队和队平了次,其他队都败给队.
C、、,队里积分最高的是胜平败.有分.
所以队出线了.
【解析】五个队分在同一小组进行单循环赛,则每个组只进行场比赛,队的积分为分,就可以得到队的胜负情况;
利用队的胜负以及另一队战绩为全胜情况,进而就可以得到其它队的胜负的情况,就可以进行判断;
利用队的胜负以及另一队战绩为积分分情况,进而就可以得到其它队的胜负的情况,就可以进行判断.
此题主要考查了推理与论证,本题将现实生活中的事件与数学思想联系起来,根据球队的积分判处出胜负的场次是解题的关键.
18.【答案】解:逆命题为:同位角相等,两直线平行,是成立,是真命题;
逆命题为:如果实数,那么,不成立,是假命题;
逆命题为:如果两个角相等,那么它们都为直角,不成立,是假命题.
【解析】把一个命题的条件和结论互换就得到它的逆命题.正确的命题叫真命题,错误的命题叫假命题.
本题主要考查了命题与定理的知识,解题的关键是了解命题与逆命题的关系,是基础题.
19.【答案】
【解析】解:选作为条件,作为结论,
故答案为:,;
证明过程如下:
在平行四边形中,对角线与交于点,
,
在和中,
,
≌,
,
.
选择作为条件,作为结论;
根据证明≌即可.
本题主要考查命题与定理知识,熟练掌握平行四边形的性质、全等三角形的判定等知识是解答此题的关键.
20.【答案】解:如图,,交于点;
如图,
与的大小为:.
因为垂线段最短.
【解析】本题考查了作图复杂作图、垂线、垂线段最短、平行线的性质,解决本题的关键是掌握垂线段最短的性质.
过点画,交于点即可;
过点画,垂足为,连接,根据垂线段最短即可判断与的大小.
21.【答案】解:.
证明:,
又是的平分线,即,
,
.
【解析】根据三角形的外角的性质,三角形的外角等于不相邻的两个内角的和,以及角平分线的定义即可得到,从而证得.
本题考查了三角形的外角的性质以及平行线的判定定理,根据三角形的外角的性质证得是关键.
22.【答案】 两直线平行,内错角相等 等量代换 同旁内角互补,两直线平行
【解析】解::
两直线平行,内错角相等,
又已知,
等量代换,
同旁内角互补,两直线平行,
故答案为:;两直线平行,内错角相等;;等量代换;同旁内角互补,两直线平行;
,
,,
平分,平分,
,,
.
由平行线的性质可得,结合已知条件可得,从而得;
由平行线的性质可得,,再由角平分线的性质可得,,从而可求解.
本题主要考查平行线的判定与性质,解答的关键是熟记平行线的判定条件与性质,并灵活运用.
23.【答案】解:,理由如下:
,,
,
,
,
,
,
;
,
,
,
.
【解析】先根据对顶角相等得出,由得出,再由同位角相等,两直线平行可得出,由平行线的性质可得,由可得,根据内错角相等,两直线平行可得;
根据得出,由得出.
本题主要考查了平行线的判定与性质,先根据题意得出是解答此题的关键.
24.【答案】解:过点作于,
,
,
解得:;
是的外角,
,
,
,
,
,
,
解得:.
【解析】过点作于,根据三角形的面积公式计算,得到答案;
根据三角形的外角性质得到,根据三角形内角和定理计算,得到答案.
本题考查的是三角形的外角性质、三角形的面积计算,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
北师大版初中数学八年级上册第七单元《平行线的证明》单元测试卷
考试范围:第七章; 考试时间:100分钟;总分120分,
学校:___________姓名:___________班级:___________考号:___________
注意:本试卷包含Ⅰ、Ⅱ两卷。第Ⅰ卷为选择题,所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题,所有答案必须填在答题卷的相应位置。答案写在试卷上均无效,不予记分。
第I卷(选择题)
一、选择题(本大题共12小题,共36分)
下列关于判断一个数学结论是否正确的叙述,正确的是
A. 只需观察得出 B. 只需依靠经验获得
C. 通过亲自试验得出 D. 必须进行有根据的证实
根据一周天可以制作出每年的“星期几密码”现已知年的“星期几密码”是“”,这组密码中从左到右的个数字依次与年的到月对应,我们可以用这组密码算出年某天是星期几.如年月日,其中月对应密码中的第二个数字“”,将数字加上日期,其和为,再把除以,得余数,则该天为星期四余数几则对应星期几,特别地,余数则对应星期天.
利用此密码算出年的世界环境日月日是
A. 星期一 B. 星期二 C. 星期四 D. 星期六
小英、小亮、小明和小华四名同学参加了“大梦杯”竞赛选拔赛,小亮和小华两个同学的得分和等于小明和小英的得分和;小英与小亮的得分和大于小明和小华的得分和;小华的得分超过小明与小亮的得分和.则这四位同学的得分由大到小的顺序是
A. 小明、小亮、小华、小英 B. 小华、小明、小亮、小英
C. 小英、小华、小亮、小明 D. 小亮、小英、小华、小明
以下四个命题:如果一个数的相反数等于它本身,则这个数是一个数的倒数等于它本身,则这个数是一个数的算术平方根等于它本身,则这个数是或如果一个数的绝对值等于它本身,则这个数是正数其中真命题有
A. 个 B. 个 C. 个 D. 个
将命题“对顶角相等”写成“如果那么”的形式,正确的是
如果两个角相等,那么它们是对顶角
如果两个角是对顶角,那么它们相等
C. 如果对顶角,那么相等
D. 如果两个角不是对顶角,那么这两个角不相等
如图,不能判定的是
A. B.
C. D.
一次数学活动中,检验两条纸带、的边线是否平行,小明和小丽采用两种不同的方法:如图,小明对纸带沿折叠,量得小丽对纸带沿折叠,发现与重合,与重合则下列判断正确的是
A. 纸带的边线平行,纸带的边线不平行
B. 纸带的边线不平行,纸带的边线平行
C. 纸带的边线都平行
D. 纸带的边线都不平行
将一块直角三角板按如图方式放置,其中,,两点分别落在直线、上,,添加下列哪一个条件可使直线
A.
B.
C.
D.
如图,下列推理及所证明的理由都正确的是
A. 若,则,理由是内错角相等,两直线平行
B. 若,则,理由是两直线平行,内错角相等
C. 若,则,理由是内错角相等,两直线平行
D. 若,则,理由是两直线平行,内错角相等
如图,,,,,的面积为,则四边形的面积为
A.
B.
C.
D.
下列判断:
三角形的三个内角中最多有一个钝角;
三角形的三个内角中至少有两个锐角;
有两个内角为和的三角形一定是钝角三角形;
直角三角形中两锐角的和为.
其中判断正确的有 .
A. 个 B. 个 C. 个 D. 个
将一把直尺和一块含和角的三角板按如图所示的位置放置,如果,那么的大小为
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
如图, .
如图,点在的延长线上,对于给出的四个条件:
;
;
;
.
能判断的有______填写序号.
命题“如果,那么,互为相反数”的逆命题为______.
天干地支纪年法是上古文明的产物,又称节气历或中国阳历有十天干与十二地支,如下表:
天干 甲 乙 丙 丁 戊 己 庚 辛 壬 癸
地支 子 丑 寅 卯 辰 巳 午 未 申 酉 戌 亥
算法如下:先用年份的尾数查出天干,再用年份除以的余数查出地支如年,尾数为戊,除以余数为,为子,那么年就是戊子年.
年是伟大、光荣、正确的中国共产党成立周年,则年是______ 年用天干地支纪年法表示
三、解答题(本大题共8小题,共72分)
有五个足球队、、、、分入同一小组进行单循环足球比赛,争夺出线权,比赛规定:胜一场得分,平一场得分,负一场得分,小组中名次在前的两个队出线,小组赛结束后,如果队的积分为分,讨论:
队的战绩是几胜,几平,几负?
如果小组赛中有一个队的战绩为全胜,队能否出线?
如果小组赛中有一个队的积分为,队能否出线?
写出下列命题的逆命题,这些逆命题都成立吗?
两直线平行,同位角相等;
如果实数,那么;
直角都相等.
如图,在平行四边形中,对角线与交于点,且,请你从,,平分中任选一个作为添加条件,另两个中的一个作为结论,组成一个真命题,并证明.
添加条件:______,结论:______;填序号
根据你所选择的条件和结论,写出证明过程.
如图,直线与直线相交于,解答下列问题.
过点画,交于点;
过点画,垂足为,连接,判断与的大小,并说明理由.
如图,,、、三点在同一直线上,,是的平分线,与平行吗?说明你的理由.
已知:如图,,.
试说明成立的理由完成下面填空
证明:
____________
又已知
____________
______
若平分,平分,且,求的度数.
如图,已知,.
判断与的位置关系,并说明理由;
若,求的度数.
如图,在中,是上一点.
若,,,,求中边上的高的长;
若,,,求的度数.
答案和解析
1.【答案】
【解析】
【分析】
本题考查了数学结论是怎样得到的,必须有严密的逻辑证明过程.要判断一个数学结论是否正确,仅仅依靠经验,观察或实验是不够的,必须每一步都要有根有据地进行推理.
【解答】
解:经验,观察或实验只能为数学活动提供思路,要想得到正确结论,每一步都要有严密的逻辑推理过程,
故选: .
2.【答案】
【解析】
【分析】
本题考查了推理与论证,关键是理解题意.根据题意得出 月对应第六个数字 ,将数字 加上日期 ,和为 ,用 除以 求出商和余数,再根据余数即可求解.
【解答】
解:依题意得: 月对应第六个数字 ,
将数字 加上日期 ,和为 ,
,
故 年的世界环境日 月 日 是星期二.
故选: .
3.【答案】
【解析】
【分析】
本题主要考查了推理与论证的问题,能够通过已知条件找出突破口,从而通过推理得出结论.
由题干中前两个条件可得小英的得分大于小华的,小亮的大于小明的,再结合第三个条件,进而可出结论.
【解答】
解:由题干中小亮和小华两个同学的得分和等于小明和小英的得分和;
小英与小亮的得分和大于小明和小华的得分和,
可得小英的得分大于小华的,小亮的大于小明的;
又有小华的得分超过小明与小亮的得分和,
所以可得四位同学的得分由大到小的顺序是小英、小华、小亮、小明.
4.【答案】
【解析】
【分析】
本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果 那么 ”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.
根据相反数的定义对 进行判断;根据 的倒数等于 可对 进行判断;根据算术平方根的定义对 进行判断;根据 的绝对值等于 可对 进行判断.
【解答】
解:如果一个数的相反数等于它本身,则这个数是 ,所以 正确;
一个数的倒数等于它本身,则这个数是 或 ,所以 错误;
一个数的算术平方根等于它本身,则这个数是 或 ,所以 正确;
如果一个数的绝对值等于它本身,则这个数是正数或 ,所以 错误.
故选 B .
5.【答案】
【解析】
【分析】
本题考查命题与定理,先把原命题分成题设和结论,然后变成如果 那么 的形式即可,注意改写过程语句要通顺.
【解答】
解:对顶角相等写成“如果 那么 ”的形式为:如果两个角是对顶角,那么它们相等;
故选 B .
6.【答案】
【解析】
【分析】
本题考查平行线的判定,解题的关键是熟练掌握基本知识,属于中考常考题型.
利用平行线的判定方法一一判断即可.
【解答】
解: 由 ,根据同位角相等两直线平行,即可判断 .
B. 由 ,根据内错角相等两直线平行,即可判断 .
C. 由 ,根据同旁内角互补两直线平行,即可判断 .
D. 由 不能判定 .
故选: .
7.【答案】
【解析】
【分析】
此题主要考查了平行线的判定以及翻折变换的性质,正确掌握翻折变换的性质是解题关键.直接利用翻折变换的性质结合平行线的判定方法得出答案.
【解析】
解:如图 所示,因为 , ,
所以 ,
所以 ,
所以 ,所以纸带 的边线不平行.
如图所示,因为与重合,与重合,
所以,,
所以,同旁内角互补,两直线平行
所以纸带的边线平行.
故选B.
8.【答案】
【解析】
【分析】
本题考查了平行线的判定,熟练掌握平行线的判定定理是解题关键 利用平行线的判定定理:内错角相等,两直线平行即可解答.
【解答】
解:因为 构成的角与 是内错角,
所以要使直线 ,只需 ,
又因为 , ,
所以可添加的条件是 .
故选 D .
9.【答案】
【解析】
【分析】
本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.根据平行线的性质,进行判断即可.
【解答】
解: 若 ,则 ,理由是两直线平行,内错角相等,故选项 A 错误;
B. 若 ,则 ,并不是 ,理由是两直线平行,内错角相等,故选项 B 错误;
C. 若 ,则 ,理由是两直线平行,内错角相等,故选项 C 错误;
D. 若 ,则 ,理由是两直线平行,内错角相等,正确;
故选: .
10.【答案】
【解析】解:,,
四边形为平行四边形,
,
,
,
点和点到的距离相等,
设点到的距离为,
的面积为,
,
解得,
四边形的面积.
故选:.
先判断四边形为平行四边形得到,则,再利用得到点和点到的距离相等,设点到的距离为,利用的面积为可计算出,然后根据平行四边形的面积公式计算四边形的面积.
本题考查了三角形的面积:三角形的面积等于底边长与高线乘积的一半,即底高.也考查了平行线的性质.
11.【答案】
【解析】
【分析】
此题考查了三角形的内角和定理.解题时要仔细分析,理解题意.因为三角形的内角和为 ,所以三角形的三个内角中最多有一个钝角,三角形的三个内角中至少有两个锐角,据此可对 作出判断;有两个内角为 和 的三角形的第三角为 ,所以一定是钝角三角形,据此可对 作出判断;因为直角三角形中有一个角等于 ,所以直角三角形中两锐角的和为 ,据此可对 作出判断.
【解答】
解:因为三角形的内角和为 ,所以三角形的三个内角中最多有一个钝角,三角形的三个内角中至少有两个锐角,所以 是正确的;
有两个内角为 和 的三角形的第三角为 ,所以一定是钝角三角形,所以 正确;
因为直角三角形中有一个角等于 ,所以直角三角形中两锐角的和为 ,所以 正确.
可得 都正确,
故选 D .
12.【答案】
【解析】
【分析】
本题主要考查平行线的性质,解题的关键是掌握两直线平行同位角相等与三角形外角的性质.
由 得 ,再根据三角形的外角性质可得答案.
【解答】
解:由题意知 ,
,
,
.
13.【答案】
【解析】略
14.【答案】
【解析】解:根据内错角相等,两直线平行即可证得;
根据内错角相等,两直线平行即可证得,不能证明;
根据同位角相等,两直线平行即可证得;
根据同旁内角互补,两直线平行即可证得,不能证明.
故答案为:.
根据平行线的判定定理进行逐一判断即可.
本题考查了平行线的判定定理,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
15.【答案】如果,互为相反数,那么
【解析】
【分析】
本题考查的是命题与定理、互逆命题,掌握逆命题的确定方法是解题的关键.
根据互逆命题的定义写出逆命题即可.
【解答】
解:命题“如果 ,那么 , 互为相反数”的逆命题为:
如果 , 互为相反数,那么 ;
故答案为:如果 , 互为相反数,那么 .
16.【答案】辛丑
【解析】解:年,尾数为辛,除以余数为,为丑,那么年就是辛丑年.
故答案为:辛丑.
先用的尾数查出天干,再用除以的余数查出地支即可.
本题是考查了推理,读懂天干地支的算法是解决本题的关键.
17.【答案】解:个队进行单循环足球比赛,
每个队间只比赛次,每个队和其他队比赛次,
设队胜,平,
,
得:,,故A队的战绩是胜平负.
小组赛中有一个队的战绩为全胜,队的积分为分,
其他队最多可以胜场比赛,故最多可得分,
队能出线;
假设是队的战绩为分.它就是胜平败.
可以看出,队只败给了队.就是说,,,都败给队了.
队里有队和队平了次,其他队都败给队.
C、、,队里积分最高的是胜平败.有分.
所以队出线了.
【解析】五个队分在同一小组进行单循环赛,则每个组只进行场比赛,队的积分为分,就可以得到队的胜负情况;
利用队的胜负以及另一队战绩为全胜情况,进而就可以得到其它队的胜负的情况,就可以进行判断;
利用队的胜负以及另一队战绩为积分分情况,进而就可以得到其它队的胜负的情况,就可以进行判断.
此题主要考查了推理与论证,本题将现实生活中的事件与数学思想联系起来,根据球队的积分判处出胜负的场次是解题的关键.
18.【答案】解:逆命题为:同位角相等,两直线平行,是成立,是真命题;
逆命题为:如果实数,那么,不成立,是假命题;
逆命题为:如果两个角相等,那么它们都为直角,不成立,是假命题.
【解析】把一个命题的条件和结论互换就得到它的逆命题.正确的命题叫真命题,错误的命题叫假命题.
本题主要考查了命题与定理的知识,解题的关键是了解命题与逆命题的关系,是基础题.
19.【答案】
【解析】解:选作为条件,作为结论,
故答案为:,;
证明过程如下:
在平行四边形中,对角线与交于点,
,
在和中,
,
≌,
,
.
选择作为条件,作为结论;
根据证明≌即可.
本题主要考查命题与定理知识,熟练掌握平行四边形的性质、全等三角形的判定等知识是解答此题的关键.
20.【答案】解:如图,,交于点;
如图,
与的大小为:.
因为垂线段最短.
【解析】本题考查了作图复杂作图、垂线、垂线段最短、平行线的性质,解决本题的关键是掌握垂线段最短的性质.
过点画,交于点即可;
过点画,垂足为,连接,根据垂线段最短即可判断与的大小.
21.【答案】解:.
证明:,
又是的平分线,即,
,
.
【解析】根据三角形的外角的性质,三角形的外角等于不相邻的两个内角的和,以及角平分线的定义即可得到,从而证得.
本题考查了三角形的外角的性质以及平行线的判定定理,根据三角形的外角的性质证得是关键.
22.【答案】 两直线平行,内错角相等 等量代换 同旁内角互补,两直线平行
【解析】解::
两直线平行,内错角相等,
又已知,
等量代换,
同旁内角互补,两直线平行,
故答案为:;两直线平行,内错角相等;;等量代换;同旁内角互补,两直线平行;
,
,,
平分,平分,
,,
.
由平行线的性质可得,结合已知条件可得,从而得;
由平行线的性质可得,,再由角平分线的性质可得,,从而可求解.
本题主要考查平行线的判定与性质,解答的关键是熟记平行线的判定条件与性质,并灵活运用.
23.【答案】解:,理由如下:
,,
,
,
,
,
,
;
,
,
,
.
【解析】先根据对顶角相等得出,由得出,再由同位角相等,两直线平行可得出,由平行线的性质可得,由可得,根据内错角相等,两直线平行可得;
根据得出,由得出.
本题主要考查了平行线的判定与性质,先根据题意得出是解答此题的关键.
24.【答案】解:过点作于,
,
,
解得:;
是的外角,
,
,
,
,
,
,
解得:.
【解析】过点作于,根据三角形的面积公式计算,得到答案;
根据三角形的外角性质得到,根据三角形内角和定理计算,得到答案.
本题考查的是三角形的外角性质、三角形的面积计算,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
