人教版数学九年级下册第二十八章 数学活动课件(共22张PPT)
文档属性
| 名称 | 人教版数学九年级下册第二十八章 数学活动课件(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-14 16:44:24 | ||
图片预览








文档简介
(共24张PPT)
数学活动
半圆形量角器,细线,小挂件(或其他小重物),软尺,利用这些小物件可以制成什么器具呢?
测角仪
今天我们就要学习利用测角仪测定实际物体的高度.
想一想
新课导入
制作测角仪,测量树的高度
活动1
阅读课本“活动1”.
1.测角仪是由哪几个部分组成的?
2.测角仪上角的读数与仰角有怎样的关系?
思考
推进新课
把一根细线固定在半圆形量角器的圆心处.
提问
如何制作一个简易的测角仪呢?
1
在细线的另一端系一个小挂件即可.
2
将仪器拿到眼前,使视线沿着仪器的直径刚好到达树的最高点(如图).
提问
如何使用测角仪呢?
答
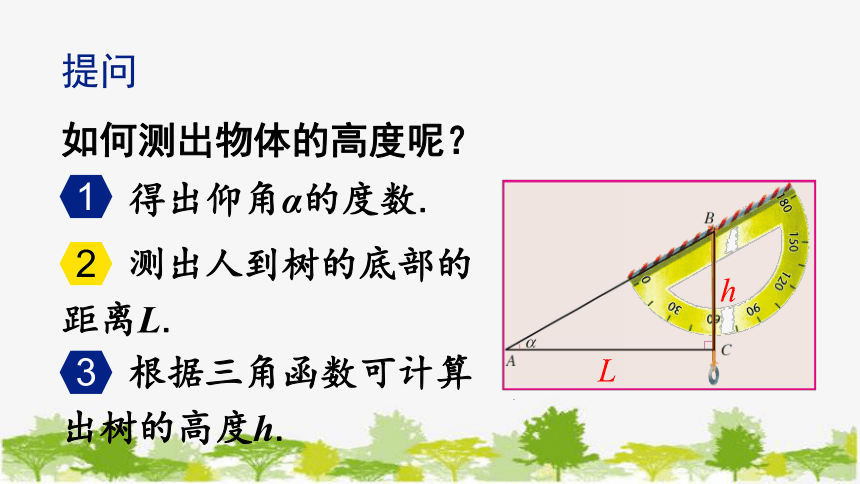
得出仰角α的度数.
提问
如何测出物体的高度呢?
1
测出人到树的底部的距离L.
2
根据三角函数可计算出树的高度h.
3
L
h
利用测角仪测量塔高
活动2
思考
若不能直接测出AN的长度,还有别的方法可以测出物体的高度吗?
具体怎么操作呢?
步骤
在塔前的平地上选择一点A,用活动1中制作的测角仪测出看塔顶的仰角α(如图).
1
步骤
在A点和塔之间选择一点B,测出你由B点看塔顶的仰角β.
2
测出A,B两点间的距离.
3
设塔高为x,测量者的身高为y,
提问
如何计算出塔的高度呢?
解
则可以得到关于x的方程:
解这个方程,就可以求出塔高x.
1.如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10 m到达B点,在B处测得树顶C的仰角为60°(A、B、D三点在同一直线上).
请你根据他们的测量数据计算这棵
树的高度(结果精确到0.1 m).
基础巩固
随堂演练
解:设CD=x.
∴AB=AD-BD,
即
在Rt△BCD中,BD=
2.如图,小明的眼睛与地面的距离(AB)是1.7 m,他调整自己的位置,设法使得三角板的一条直角边保持水平,且斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M的仰角为45°;小红眼睛与地面的距离(CD)是1.5 m,用同样的方法测得旗杆顶端M的仰角为30°.两人相距28 m
且位于旗杆两侧(点B、N、D
在同一条直线上).求出旗杆
MN的高度(结果精确到0.1 m).
解:如图所示,作AE⊥MN于E,CF⊥MN于F.设MN=x.
在Rt△MAE中,
ME=MN-EN=MN-AB=x-1.7,∠MAE=45°,
∴AE=ME=x-1.7.
在Rt△MCF中,MF=MN-NF=MN-CD=x-1.5,∠MCF=30°,
∴x≈11.8.∴MN≈11.8(m).
因此,旗杆MN的高度约为11.8 m.
又∵BD=BN+ND=AE+FC,
∴x-1.7+ (x-1.5)=28.
综合应用
3.大楼AD的高为100米,远处有一塔BC,某人在楼底A处测得塔顶B处的仰角为60°,爬到楼顶D处测得塔顶B的仰角为30°,求塔BC的高度.
解:作DE⊥BC于E.
设BC=x,在Rt△ABC中,
在Rt△BDE中,
BE=BC-EC=BC-AD
=x-100.
又∵DE=AC,∴ x = (x-100),
∴x = 150,BC = 150(米).
因此,塔BC的高度为150米.
设塔高为x,测量者的身高为y,
解
课堂小结
某数学兴趣小组在河边的一点A处测得河对岸小山顶上一座铁塔的塔顶C的仰角为60°、塔底B的仰角为45°,已知铁塔的高度BC为20m,
你能根据以上数据求出小山的高
BD吗?若不能,请说明理由;若
能,请求出小山的高BD(精确到
0.1 m).
过程如下:
设AD=x,在Rt△ABD中,
∠BAD=45°,∴BD=AD=x.
解:能;
在Rt△ACD中,∠CAD=60°,
∴CD=AD·tan60°= x.
又∵BC=CD-BD,∴ x-x=20.
∴x≈27.3,BD≈27.3(m).
因此,小山的高BD约为27.3 m.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
数学活动
半圆形量角器,细线,小挂件(或其他小重物),软尺,利用这些小物件可以制成什么器具呢?
测角仪
今天我们就要学习利用测角仪测定实际物体的高度.
想一想
新课导入
制作测角仪,测量树的高度
活动1
阅读课本“活动1”.
1.测角仪是由哪几个部分组成的?
2.测角仪上角的读数与仰角有怎样的关系?
思考
推进新课
把一根细线固定在半圆形量角器的圆心处.
提问
如何制作一个简易的测角仪呢?
1
在细线的另一端系一个小挂件即可.
2
将仪器拿到眼前,使视线沿着仪器的直径刚好到达树的最高点(如图).
提问
如何使用测角仪呢?
答
得出仰角α的度数.
提问
如何测出物体的高度呢?
1
测出人到树的底部的距离L.
2
根据三角函数可计算出树的高度h.
3
L
h
利用测角仪测量塔高
活动2
思考
若不能直接测出AN的长度,还有别的方法可以测出物体的高度吗?
具体怎么操作呢?
步骤
在塔前的平地上选择一点A,用活动1中制作的测角仪测出看塔顶的仰角α(如图).
1
步骤
在A点和塔之间选择一点B,测出你由B点看塔顶的仰角β.
2
测出A,B两点间的距离.
3
设塔高为x,测量者的身高为y,
提问
如何计算出塔的高度呢?
解
则可以得到关于x的方程:
解这个方程,就可以求出塔高x.
1.如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10 m到达B点,在B处测得树顶C的仰角为60°(A、B、D三点在同一直线上).
请你根据他们的测量数据计算这棵
树的高度(结果精确到0.1 m).
基础巩固
随堂演练
解:设CD=x.
∴AB=AD-BD,
即
在Rt△BCD中,BD=
2.如图,小明的眼睛与地面的距离(AB)是1.7 m,他调整自己的位置,设法使得三角板的一条直角边保持水平,且斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M的仰角为45°;小红眼睛与地面的距离(CD)是1.5 m,用同样的方法测得旗杆顶端M的仰角为30°.两人相距28 m
且位于旗杆两侧(点B、N、D
在同一条直线上).求出旗杆
MN的高度(结果精确到0.1 m).
解:如图所示,作AE⊥MN于E,CF⊥MN于F.设MN=x.
在Rt△MAE中,
ME=MN-EN=MN-AB=x-1.7,∠MAE=45°,
∴AE=ME=x-1.7.
在Rt△MCF中,MF=MN-NF=MN-CD=x-1.5,∠MCF=30°,
∴x≈11.8.∴MN≈11.8(m).
因此,旗杆MN的高度约为11.8 m.
又∵BD=BN+ND=AE+FC,
∴x-1.7+ (x-1.5)=28.
综合应用
3.大楼AD的高为100米,远处有一塔BC,某人在楼底A处测得塔顶B处的仰角为60°,爬到楼顶D处测得塔顶B的仰角为30°,求塔BC的高度.
解:作DE⊥BC于E.
设BC=x,在Rt△ABC中,
在Rt△BDE中,
BE=BC-EC=BC-AD
=x-100.
又∵DE=AC,∴ x = (x-100),
∴x = 150,BC = 150(米).
因此,塔BC的高度为150米.
设塔高为x,测量者的身高为y,
解
课堂小结
某数学兴趣小组在河边的一点A处测得河对岸小山顶上一座铁塔的塔顶C的仰角为60°、塔底B的仰角为45°,已知铁塔的高度BC为20m,
你能根据以上数据求出小山的高
BD吗?若不能,请说明理由;若
能,请求出小山的高BD(精确到
0.1 m).
过程如下:
设AD=x,在Rt△ABD中,
∠BAD=45°,∴BD=AD=x.
解:能;
在Rt△ACD中,∠CAD=60°,
∴CD=AD·tan60°= x.
又∵BC=CD-BD,∴ x-x=20.
∴x≈27.3,BD≈27.3(m).
因此,小山的高BD约为27.3 m.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
