苏科版数学九年级下册 6.4 第1课时 利用平行证相似 同步课时练习(word版 含解析)
文档属性
| 名称 | 苏科版数学九年级下册 6.4 第1课时 利用平行证相似 同步课时练习(word版 含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 240.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-15 06:41:25 | ||
图片预览


文档简介
6.4 第1课时 利用平行证相似
知识点 1 平行线分线段成比例的基本事实
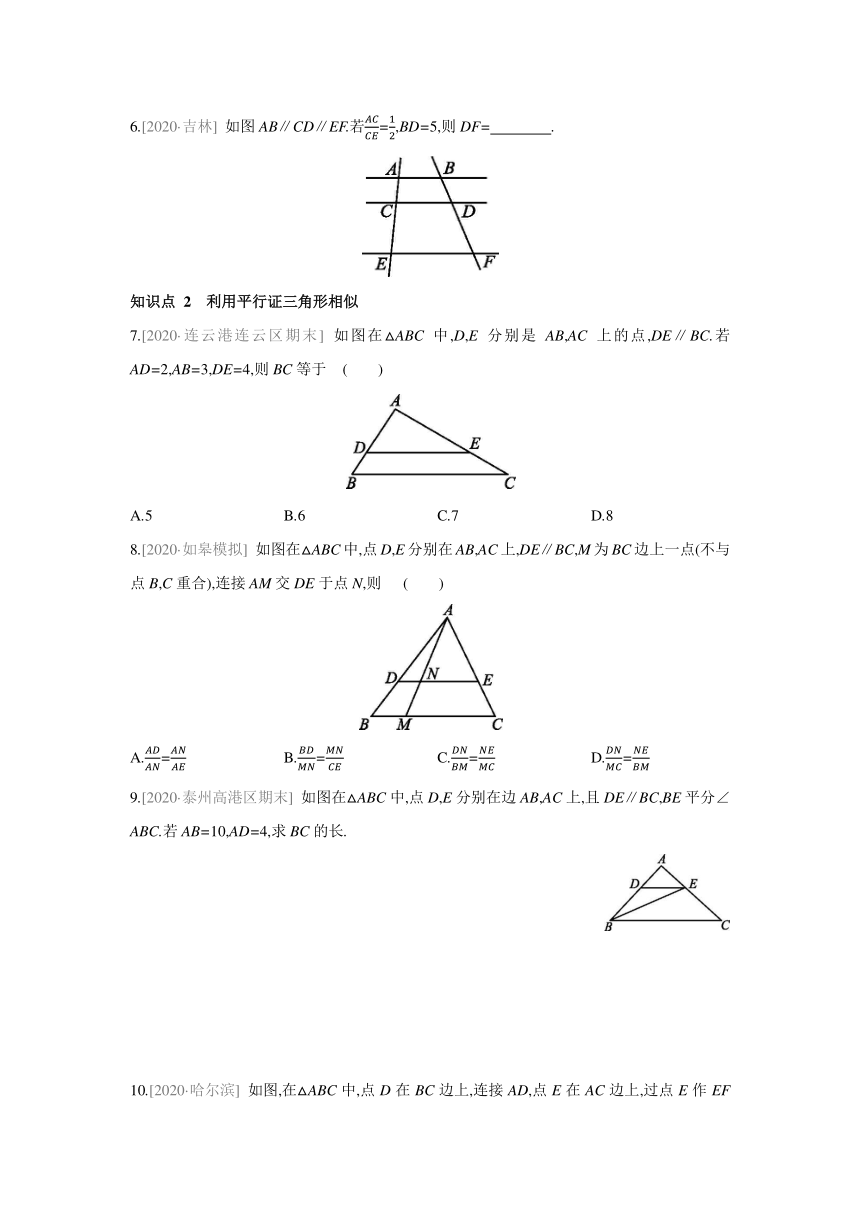
1.如图a∥b∥c,直线m,n与直线a,b,c分别相交于点A,B,C和点D,E,F.
(1)若AB=BC,则DE EF(填“>”“<”或“=”);
(2)= ,= ,= .
2.如图AB∥CD∥EF,下面等式成立的是 ( )
A.AC·CE=BD·DF B.AC·AE=BD·BF
C.AC·DF=CE·BD D.CD2=AB·EF
3.[2021·盐城期末] 如图已知直线l1∥l2∥l3,若AB∶BC=2∶3,则DE∶DF的值为( )
A.3∶2 B.2∶3 C.2∶5 D.3∶5
4.如图已知AB∥CD,AC与BD交于点O,则下列比例式中成立的是 ( )
A.= B.= C.= D.=
5.[2021·无锡锡山区期中] 如图在△ABC中,点D,E分别在边AB,BC上,DE∥AC,若DB=4,AB=6,BE=3,则BC的长是 .
6.[2020·吉林] 如图AB∥CD∥EF.若=,BD=5,则DF= .
知识点 2 利用平行证三角形相似
7.[2020·连云港连云区期末] 如图在△ABC中,D,E分别是AB,AC上的点,DE∥BC.若AD=2,AB=3,DE=4,则BC等于 ( )
A.5 B.6 C.7 D.8
8.[2020·如皋模拟] 如图在△ABC中,点D,E分别在AB,AC上,DE∥BC,M为BC边上一点(不与点B,C重合),连接AM交DE于点N,则 ( )
A.= B.= C.= D.=
9.[2020·泰州高港区期末] 如图在△ABC中,点D,E分别在边AB,AC上,且DE∥BC,BE平分∠ABC.若AB=10,AD=4,求BC的长.
10.[2020·哈尔滨] 如图,在△ABC中,点D在BC边上,连接AD,点E在AC边上,过点E作EF∥BC,交AD于点F,过点E作EG∥AB,交BC于点G,则下列式子一定正确的是( )
A.= B.= C.= D.=
11.[2021·泰州姜堰区期末] 如图,AD是△ABC的中线,点E在边AC上,BE交AD于点F,若AC=4AE,AD=3 cm,则AF的长度为 cm.
12.如图,直线l1,l2,l3分别交直线l4于点A,B,C,交直线l5于点D,E,F,l4,l5交于点O,且
l1∥l2∥l3.已知EF∶DF=5∶8,AC=24.
(1)求AB的长;
(2)当AD=4,BE=1时,求CF的长.
13.[2020·宜兴期末] 如图,在△ABC中,D,E分别为BC,AC上的点,AD与BE相交于点G,且=4,=.
(1)求的值;
(2)若CE=5 cm,求AC的长.
14.如图,在△ABC中,∠C=90°,AB=10,BC=6,点P从点A出发,沿折线AB—BC向终点C运动,在AB上以每秒5个单位长度的速度运动,在BC上以每秒3个单位长度的速度运动.点Q从点C出发,沿CA方向以每秒个单位长度的速度运动.P,Q两点同时出发,当点P停止运动时,点Q也随之停止运动.设点P运动的时间为t秒.
(1)求线段AQ的长(用含t的代数式表示);
(2)连接PQ,当PQ与△ABC的一边平行时,求t的值.
答案
6.4 第1课时 利用平行证相似
1.(1)= (2)
2.C ∵AB∥CD∥EF,∴=,∴AC·DF=CE·BD.故选C.
3.C ∵l1∥l2∥l3,AB∶BC=2∶3,
∴==,∴=.故选C.
4.A
5.4.5 ∵DE∥AC,∴DB∶AB=BE∶BC.∵DB=4,AB=6,BE=3,∴4∶6=3∶BC,
∴BC=4.5.
6.10 ∵AB∥CD∥EF,∴==,∴DF=2BD=2×5=10.
7.B ∵DE∥BC,∴△ADE∽△ABC,
∴=,即=,解得BC=6.故选B.
8.C ∵DN∥BM,
∴△ADN∽△ABM,
∴=.
∵NE∥MC,∴△ANE∽△AMC,
∴=,
∴=.故选C.
9.解:∵AB=10,AD=4,
∴BD=AB-AD=6.
∵DE∥BC,
∴∠DEB=∠EBC.
∵BE平分∠ABC,
∴∠DBE=∠EBC,
∴∠DEB=∠DBE,
∴DE=BD=6.
∵DE∥BC,
∴△ADE∽△ABC,
∴=,即=,
∴BC=15.
10.C ∵EF∥BC,∴=.
∵EG∥AB,∴=,∴=.
故选C.
11.1.2 过点D作DG∥AC交BE于点G,如图.
∵AD是△ABC的中线,∴BD=CD.
∵AC=4AE,∴CE=3AE.
∵DG∥CE,∴==,
即DG=CE,∴DG=AE.
∵DG∥AE,
∴===,
∴=,
∴AF=AD=×3=1.2(cm).
故答案为1.2.
12. (1)由平行线分线段成比例的基本事实可以直接得出结论;(2)注意到条件中的AD,BE的长,则考虑运用平行线得相似,转化已知条件.
解:(1)∵l1∥l2∥l3,EF∶DF=5∶8,
∴==.
又∵AC=24,∴=,∴BC=15,
∴AB=AC-BC=24-15=9.
(2)∵l1∥l2,∴△OBE∽△OAD,
∴==,∴=,∴OB=3,
∴OC=BC-OB=15-3=12.
∵l2∥l3,∴△OEB∽△OFC,
∴===,
∴=,∴CF=4.
13.解:(1)如图,过点D作DF∥BE交AC于点F,
则==4,∴AE=4EF.
∵DF∥BE,
∴==,∴CE=EF,
∴==.
(2)∵=,CE=5 cm,
∴=,解得AE=8(cm),
∴AC=AE+CE=8+5=13(cm).
14.解:(1)在Rt△ABC中,由勾股定理,得AC===8.
∵点Q从点C出发,沿CA方向以每秒个单位长度的速度运动,
∴运动t秒后,CQ=t,
∴AQ=AC-CQ=8-t.
(2)分两种情况讨论如下:
如图①,若PQ∥BC,则△APQ∽△ABC,
从而=,即=,解得t=;
如图②,若PQ∥AB,则△CPQ∽△CBA,从而=,
即=,解得t=3.
综上,当PQ与△ABC的一边平行时,t的值为或3.
知识点 1 平行线分线段成比例的基本事实
1.如图a∥b∥c,直线m,n与直线a,b,c分别相交于点A,B,C和点D,E,F.
(1)若AB=BC,则DE EF(填“>”“<”或“=”);
(2)= ,= ,= .
2.如图AB∥CD∥EF,下面等式成立的是 ( )
A.AC·CE=BD·DF B.AC·AE=BD·BF
C.AC·DF=CE·BD D.CD2=AB·EF
3.[2021·盐城期末] 如图已知直线l1∥l2∥l3,若AB∶BC=2∶3,则DE∶DF的值为( )
A.3∶2 B.2∶3 C.2∶5 D.3∶5
4.如图已知AB∥CD,AC与BD交于点O,则下列比例式中成立的是 ( )
A.= B.= C.= D.=
5.[2021·无锡锡山区期中] 如图在△ABC中,点D,E分别在边AB,BC上,DE∥AC,若DB=4,AB=6,BE=3,则BC的长是 .
6.[2020·吉林] 如图AB∥CD∥EF.若=,BD=5,则DF= .
知识点 2 利用平行证三角形相似
7.[2020·连云港连云区期末] 如图在△ABC中,D,E分别是AB,AC上的点,DE∥BC.若AD=2,AB=3,DE=4,则BC等于 ( )
A.5 B.6 C.7 D.8
8.[2020·如皋模拟] 如图在△ABC中,点D,E分别在AB,AC上,DE∥BC,M为BC边上一点(不与点B,C重合),连接AM交DE于点N,则 ( )
A.= B.= C.= D.=
9.[2020·泰州高港区期末] 如图在△ABC中,点D,E分别在边AB,AC上,且DE∥BC,BE平分∠ABC.若AB=10,AD=4,求BC的长.
10.[2020·哈尔滨] 如图,在△ABC中,点D在BC边上,连接AD,点E在AC边上,过点E作EF∥BC,交AD于点F,过点E作EG∥AB,交BC于点G,则下列式子一定正确的是( )
A.= B.= C.= D.=
11.[2021·泰州姜堰区期末] 如图,AD是△ABC的中线,点E在边AC上,BE交AD于点F,若AC=4AE,AD=3 cm,则AF的长度为 cm.
12.如图,直线l1,l2,l3分别交直线l4于点A,B,C,交直线l5于点D,E,F,l4,l5交于点O,且
l1∥l2∥l3.已知EF∶DF=5∶8,AC=24.
(1)求AB的长;
(2)当AD=4,BE=1时,求CF的长.
13.[2020·宜兴期末] 如图,在△ABC中,D,E分别为BC,AC上的点,AD与BE相交于点G,且=4,=.
(1)求的值;
(2)若CE=5 cm,求AC的长.
14.如图,在△ABC中,∠C=90°,AB=10,BC=6,点P从点A出发,沿折线AB—BC向终点C运动,在AB上以每秒5个单位长度的速度运动,在BC上以每秒3个单位长度的速度运动.点Q从点C出发,沿CA方向以每秒个单位长度的速度运动.P,Q两点同时出发,当点P停止运动时,点Q也随之停止运动.设点P运动的时间为t秒.
(1)求线段AQ的长(用含t的代数式表示);
(2)连接PQ,当PQ与△ABC的一边平行时,求t的值.
答案
6.4 第1课时 利用平行证相似
1.(1)= (2)
2.C ∵AB∥CD∥EF,∴=,∴AC·DF=CE·BD.故选C.
3.C ∵l1∥l2∥l3,AB∶BC=2∶3,
∴==,∴=.故选C.
4.A
5.4.5 ∵DE∥AC,∴DB∶AB=BE∶BC.∵DB=4,AB=6,BE=3,∴4∶6=3∶BC,
∴BC=4.5.
6.10 ∵AB∥CD∥EF,∴==,∴DF=2BD=2×5=10.
7.B ∵DE∥BC,∴△ADE∽△ABC,
∴=,即=,解得BC=6.故选B.
8.C ∵DN∥BM,
∴△ADN∽△ABM,
∴=.
∵NE∥MC,∴△ANE∽△AMC,
∴=,
∴=.故选C.
9.解:∵AB=10,AD=4,
∴BD=AB-AD=6.
∵DE∥BC,
∴∠DEB=∠EBC.
∵BE平分∠ABC,
∴∠DBE=∠EBC,
∴∠DEB=∠DBE,
∴DE=BD=6.
∵DE∥BC,
∴△ADE∽△ABC,
∴=,即=,
∴BC=15.
10.C ∵EF∥BC,∴=.
∵EG∥AB,∴=,∴=.
故选C.
11.1.2 过点D作DG∥AC交BE于点G,如图.
∵AD是△ABC的中线,∴BD=CD.
∵AC=4AE,∴CE=3AE.
∵DG∥CE,∴==,
即DG=CE,∴DG=AE.
∵DG∥AE,
∴===,
∴=,
∴AF=AD=×3=1.2(cm).
故答案为1.2.
12. (1)由平行线分线段成比例的基本事实可以直接得出结论;(2)注意到条件中的AD,BE的长,则考虑运用平行线得相似,转化已知条件.
解:(1)∵l1∥l2∥l3,EF∶DF=5∶8,
∴==.
又∵AC=24,∴=,∴BC=15,
∴AB=AC-BC=24-15=9.
(2)∵l1∥l2,∴△OBE∽△OAD,
∴==,∴=,∴OB=3,
∴OC=BC-OB=15-3=12.
∵l2∥l3,∴△OEB∽△OFC,
∴===,
∴=,∴CF=4.
13.解:(1)如图,过点D作DF∥BE交AC于点F,
则==4,∴AE=4EF.
∵DF∥BE,
∴==,∴CE=EF,
∴==.
(2)∵=,CE=5 cm,
∴=,解得AE=8(cm),
∴AC=AE+CE=8+5=13(cm).
14.解:(1)在Rt△ABC中,由勾股定理,得AC===8.
∵点Q从点C出发,沿CA方向以每秒个单位长度的速度运动,
∴运动t秒后,CQ=t,
∴AQ=AC-CQ=8-t.
(2)分两种情况讨论如下:
如图①,若PQ∥BC,则△APQ∽△ABC,
从而=,即=,解得t=;
如图②,若PQ∥AB,则△CPQ∽△CBA,从而=,
即=,解得t=3.
综上,当PQ与△ABC的一边平行时,t的值为或3.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
