苏科版数学九年级下册 6.2 黄金分割同步 课时练习(word版 含解析)
文档属性
| 名称 | 苏科版数学九年级下册 6.2 黄金分割同步 课时练习(word版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 97.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-15 00:00:00 | ||
图片预览

文档简介
6.2 黄金分割
知识点1 黄金分割
1.[2021·宜兴期中] 已知点P是线段AB的一个黄金分割点(APA. B. C. D.
2.[教材例题变式] [2020·徐州期末] 点B在线段AC上,且=.若AC=4 cm,则BC=
cm.
知识点2 黄金矩形
3.[2020·苏州工业园区期末] 小明同学发现自己一本书的宽与长之比是黄金比(约为0.618).已知这本书的长为20 cm,则它的宽约为 ( )
A.12.36 cm B.13.6 cm C.32.386 cm D.7.64 cm
4.若一个矩形的宽与长的比为(-1)∶2,则称这个矩形是黄金矩形.如图示,四边形ABCD是黄金矩形,且=,将矩形ABCD剪裁掉一个正方形ADFE后,剩余的矩形BCFE是不是黄金矩形 请说明理由.
5.[2021·苏州相城区期末] 如图已知点E是正方形ABCD的边AB上的黄金分割点,且AE>EB,若S1表示以AE为边的正方形的面积,S2表示以BC为长,BE为宽的矩形的面积,S3表示正方形ABCD除去S1和S2剩余的面积,则S3∶S2的值为 ( )
A. B. C. D.
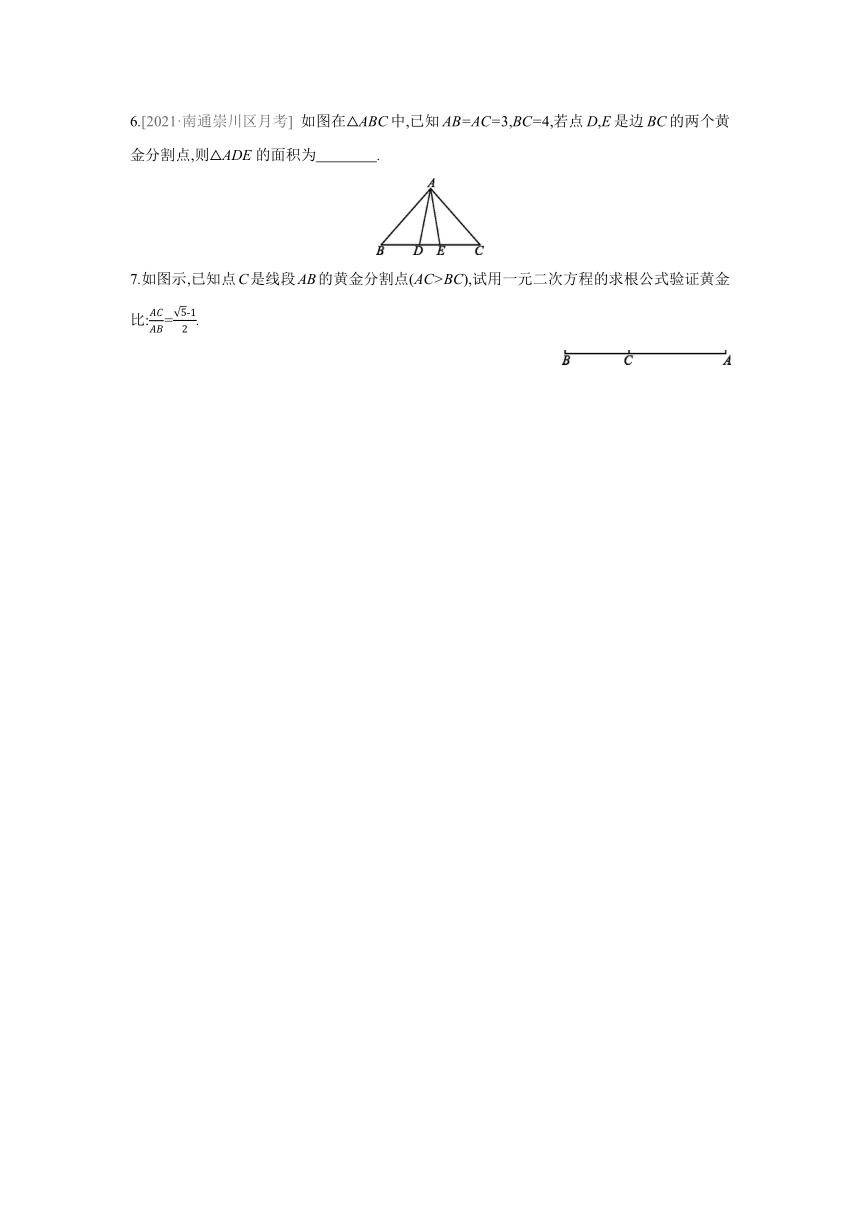
6.[2021·南通崇川区月考] 如图在△ABC中,已知AB=AC=3,BC=4,若点D,E是边BC的两个黄金分割点,则△ADE的面积为 .
7.如图示,已知点C是线段AB的黄金分割点(AC>BC),试用一元二次方程的求根公式验证黄金比:=.
答案
6.2 黄金分割
1.A ∵P是线段AB的一个黄金分割点(AP2.6-2 ∵=,∴B为AC的黄金分割点,且AB>BC,∴AB=AC=2-2cm,
∴BC=AC-AB=4-(2-2)=(6-2)cm.
3.A ∵书的宽与长之比为黄金比,书的长为20 cm,
∴书的宽约为20×0.618=12.36(cm).故选A.
4.解:是.理由:设矩形ABCD的AB边的长为x.
∵四边形ABCD为黄金矩形,且=,
∴BC=AD=x.
∵四边形ADFE是正方形,
∴AE=AD=x,
∴BE=AB-AE=x-x=x,
∴==,
∴剩余的矩形BCFE是黄金矩形.
5.A 如图,设AB=1.
∵点E是正方形ABCD的边AB上的黄金分割点,且AE>EB,
∴AE=GF=AB=,
∴BE=FH=AB-AE=,
∴S3∶S2=(GF·FH)∶(BC·BE)=×∶1×=.故选A.
6.10-4 过点A作AH⊥BC于点H,如图.
∵AB=AC,∴BH=CH=BC=2.
在Rt△ABH中,AH===.
∵D,E是边BC的两个黄金分割点,
∴CD=BE=BC=×4=2-2,
∴BD=BC-CD=4-(2-2)=6-2,
∴DE=BE-BD=2-2)=4-8,
故S△ADE=DE·AH=×(4-8)×=10-4.
7.解:设AB=1,AC=x,则有BC=1-x.
∵点C是线段AB的黄金分割点(AC>BC),
∴=,
∴AC2=BC·AB,∴x2=(1-x)×1,
整理,得x2+x-1=0,
解得x1=,x2=(舍去).
∴AC=,
∴=.
知识点1 黄金分割
1.[2021·宜兴期中] 已知点P是线段AB的一个黄金分割点(AP
2.[教材例题变式] [2020·徐州期末] 点B在线段AC上,且=.若AC=4 cm,则BC=
cm.
知识点2 黄金矩形
3.[2020·苏州工业园区期末] 小明同学发现自己一本书的宽与长之比是黄金比(约为0.618).已知这本书的长为20 cm,则它的宽约为 ( )
A.12.36 cm B.13.6 cm C.32.386 cm D.7.64 cm
4.若一个矩形的宽与长的比为(-1)∶2,则称这个矩形是黄金矩形.如图示,四边形ABCD是黄金矩形,且=,将矩形ABCD剪裁掉一个正方形ADFE后,剩余的矩形BCFE是不是黄金矩形 请说明理由.
5.[2021·苏州相城区期末] 如图已知点E是正方形ABCD的边AB上的黄金分割点,且AE>EB,若S1表示以AE为边的正方形的面积,S2表示以BC为长,BE为宽的矩形的面积,S3表示正方形ABCD除去S1和S2剩余的面积,则S3∶S2的值为 ( )
A. B. C. D.
6.[2021·南通崇川区月考] 如图在△ABC中,已知AB=AC=3,BC=4,若点D,E是边BC的两个黄金分割点,则△ADE的面积为 .
7.如图示,已知点C是线段AB的黄金分割点(AC>BC),试用一元二次方程的求根公式验证黄金比:=.
答案
6.2 黄金分割
1.A ∵P是线段AB的一个黄金分割点(AP
∴BC=AC-AB=4-(2-2)=(6-2)cm.
3.A ∵书的宽与长之比为黄金比,书的长为20 cm,
∴书的宽约为20×0.618=12.36(cm).故选A.
4.解:是.理由:设矩形ABCD的AB边的长为x.
∵四边形ABCD为黄金矩形,且=,
∴BC=AD=x.
∵四边形ADFE是正方形,
∴AE=AD=x,
∴BE=AB-AE=x-x=x,
∴==,
∴剩余的矩形BCFE是黄金矩形.
5.A 如图,设AB=1.
∵点E是正方形ABCD的边AB上的黄金分割点,且AE>EB,
∴AE=GF=AB=,
∴BE=FH=AB-AE=,
∴S3∶S2=(GF·FH)∶(BC·BE)=×∶1×=.故选A.
6.10-4 过点A作AH⊥BC于点H,如图.
∵AB=AC,∴BH=CH=BC=2.
在Rt△ABH中,AH===.
∵D,E是边BC的两个黄金分割点,
∴CD=BE=BC=×4=2-2,
∴BD=BC-CD=4-(2-2)=6-2,
∴DE=BE-BD=2-2)=4-8,
故S△ADE=DE·AH=×(4-8)×=10-4.
7.解:设AB=1,AC=x,则有BC=1-x.
∵点C是线段AB的黄金分割点(AC>BC),
∴=,
∴AC2=BC·AB,∴x2=(1-x)×1,
整理,得x2+x-1=0,
解得x1=,x2=(舍去).
∴AC=,
∴=.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
