苏科版数学九年级下册 6.4 第2课时 利用两角证相似 同步课时练习(word版 含解析)
文档属性
| 名称 | 苏科版数学九年级下册 6.4 第2课时 利用两角证相似 同步课时练习(word版 含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 243.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-15 06:44:37 | ||
图片预览



文档简介
第2课时 利用两角证相似
知识点 1 判定两个三角形相似
1.在△ABC和△A'B'C'中,若∠A=68°,∠B=40°,∠A'=68°,∠C'=72°,则这两个三角形 ( )
A.不相似 B.相似 C.全等 D.无法确定
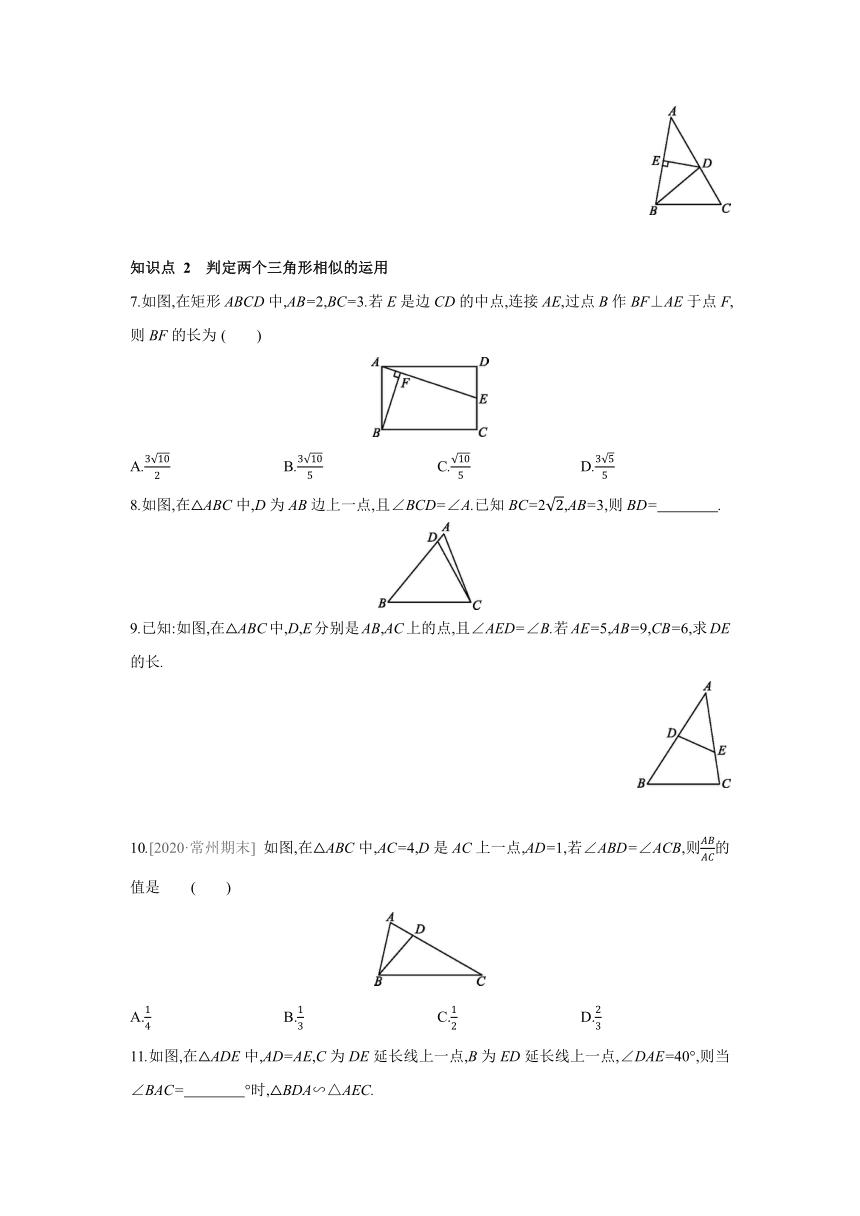
2.[2020·东台期末] 如图,在△ABC中,点D在AB边上,点E在AC边上,且∠1=∠2=
∠3,则下列结论中不正确的是 ( )
A.△ADE∽△ABC
B.△ADE∽△ACD
C.△ADE∽△EDC
D.△ABC∽△ACD 3.[2021·南通崇川区月考] 如图,在△ABC中,D,E两点分别在BC,AC上,且AD平分
∠BAC,若∠ABE=∠C,BE与AD相交于点F,则图中相似三角形的对数是 ( )
A.1 B.2 C.3 D.4
图 4.[教材练习第2题变式] [2020·昆山期末] 如图,DE∥BC.若EC=3EA,则AB= ,BC= .
5.[2021·淮安期末] 如图,在矩形ABCD中,E为AD上一点,EF⊥EC交AB于点F,连接FC.求证:△AEF∽△DCE.
6.如图,在△ABC中,∠ABC=80°,∠A=40°,AB的垂直平分线DE分别交AC,AB于点D,E,连接BD.求证:△ABC∽△BDC.
知识点 2 判定两个三角形相似的运用
7.如图,在矩形ABCD中,AB=2,BC=3.若E是边CD的中点,连接AE,过点B作BF⊥AE于点F,则BF的长为 ( )
A. B. C. D.
8.如图,在△ABC中,D为AB边上一点,且∠BCD=∠A.已知BC=2,AB=3,则BD= .
9.已知:如图,在△ABC中,D,E分别是AB,AC上的点,且∠AED=∠B.若AE=5,AB=9,CB=6,求DE的长.
10.[2020·常州期末] 如图,在△ABC中,AC=4,D是AC上一点,AD=1,若∠ABD=∠ACB,则的值是 ( )
A. B. C. D.
11.如图,在△ADE中,AD=AE,C为DE延长线上一点,B为ED延长线上一点,∠DAE=40°,则当∠BAC= °时,△BDA∽△AEC.
12.[2021·淮安淮安区期末] 如图,在△ABC中,D是BC上一点,∠DAC=∠B,E为AB上一点.
(1)求证:△CAD∽△CBA;
(2)若BD=10,DC=8,求AC的长;
(3)在(2)的条件下,若DE∥AC,AE=4,求BE的长.
13.如图,在☉O中,弦AB,CD相交于点P.求证:PA·PB=PC·PD.
14.[2020·南京期末] 如图,在等边三角形ABC中,P为BC上一点,D为AC上一点,且
∠APD=60°,2BP=3CD,BP=1.
(1)求证:△ABP∽△PCD;
(2)求△ABC的边长.
15.[2020·南京玄武区期末] 如图,在△ABC中,AB=3,AC=4,BC=6,D是BC上一点,CD=2,过点D的直线l将△ABC分成两部分,使其所分成的三角形与△ABC相似,若直线l与△ABC另一边的交点为P,则DP的长为 .
答案
第2课时 利用两角证相似
1.B
2.C ∵∠1=∠2,∠A=∠A,
∴△ADE∽△ABC.
∵∠1=∠3,∠A=∠A,
∴△ADE∽△ACD.
∵∠2=∠3,∠A=∠A,
∴△ABC∽△ACD.
无法判定△ADE∽△EDC.故选C.
3.C 如图,①在△ABE与△ACB中,∠ABE=∠C,∠BAE=∠CAB,则△ABE∽△ACB;
②∵AD平分∠BAC,∴∠1=∠2.又∵∠ABF=∠C,∴△ABF∽△ACD;
③∵△ABE∽△ACB,∴∠BEA=∠ABD.
又∵∠1=∠2,∴△AEF∽△ABD,综合①②③知,共有3对相似三角形.故选C.
4.20 24 由EC=3EA,得AC=2AE.∵DE∥BC,∴∠D=∠B,∠E=∠C,∴△AED∽
△ACB,∴===,即==,∴AB=20,BC=24.
5.证明:∵∠FEC=90°,
∴∠AEF+∠DEC=90°.
∵四边形ABCD是矩形,∴∠A=∠D=90°.
∵∠A+∠AFE+∠AEF=180°,
∴∠AFE+∠AEF=90°,
∴∠DEC=∠AFE.
又∵∠A=∠D,∴△AEF∽△DCE.
6.证明:∵DE是AB的垂直平分线,
∴AD=BD,
∴∠ABD=∠A=40°.
∵∠ABC=80°,
∴∠DBC=40°,
∴∠A=∠DBC.
又∵∠C=∠C,
∴△ABC∽△BDC.
7.B 在矩形ABCD中,∵E是边CD的中点,CD=AB=2,∴DE=1.
在Rt△ADE中,AE==.∵BF⊥AE,∴∠AFB=∠D=90°.
∵∠DAE+∠BAE=90°,∠FBA+∠BAE=90°,∴∠DAE=∠FBA,∴△ADE∽△BFA,从而=,∴=,∴BF=.
8. ∵∠BCD=∠A,∠B=∠B,
∴△DCB∽△CAB,∴=,
∴=,∴BD=.
9.解:∵∠AED=∠B,∠A=∠A,
∴△AED∽△ABC,
∴=.
∵AE=5,AB=9,CB=6,
∴=,解得DE=.
10.C ∵∠ABD=∠ACB,∠BAD=∠CAB,∴△ABD∽△ACB,∴=,∴=,
∴AB=2(负值已舍去),∴=.故选C.
11.110 ∵AD=AE,∠DAE=40°,
∴∠ADE=∠AED=70°,
∴∠B+∠BAD=70°.
∵△BDA∽△AEC,
∴∠B=∠EAC,
∴∠EAC+∠BAD=∠B+∠BAD=70°,
∴∠BAC=(∠EAC+∠BAD)+∠DAE=70°+40°=110°.故答案为110.
12.解:(1)证明:∵∠DAC=∠B,∠C=∠C,
∴△CAD∽△CBA.
(2)∵△CAD∽△CBA,
∴=,
∴=,∴AC=12(负值已舍去).
(3)∵DE∥AC,∴=,
即=,∴BE=5.
13.证明:如图,连接AC,BD,则∠CAB=∠BDC.
又∵∠APC=∠DPB,
∴△APC∽△DPB,
∴=,
∴PA·PB=PC·PD.
14.解:(1)证明:∵△ABC是等边三角形,
∴∠B=∠C=60°.
∵∠BPA+∠APD+∠DPC=180°,且∠APD=60°,
∴∠BPA+∠DPC=120°.
∵∠DPC+∠C+∠CDP=180°,
∴∠DPC+∠CDP=120°,∴∠BPA=∠CDP,∴△ABP∽△PCD.
(2)∵2BP=3CD,且BP=1,∴CD=.
∵△ABP∽△PCD,∴=.
设AB=x,则PC=x-1,∴=,∴x=3,即AB=3,∴△ABC的边长为3.
15.1或或 如图①,若DP∥AB,
则△CDP∽△CBA,
∴=,
即=,∴DP=1.
如图②,若DP∥AC,
则△BDP∽△BCA,
∴=,
即=,
∴PD=.
如图③,若∠CDP=∠A,
∵∠C=∠C,
∴△CDP∽△CAB,
∴=,
即=,
∴PD=.
综上所述,DP的长为1或或.
故答案为1或或.
知识点 1 判定两个三角形相似
1.在△ABC和△A'B'C'中,若∠A=68°,∠B=40°,∠A'=68°,∠C'=72°,则这两个三角形 ( )
A.不相似 B.相似 C.全等 D.无法确定
2.[2020·东台期末] 如图,在△ABC中,点D在AB边上,点E在AC边上,且∠1=∠2=
∠3,则下列结论中不正确的是 ( )
A.△ADE∽△ABC
B.△ADE∽△ACD
C.△ADE∽△EDC
D.△ABC∽△ACD 3.[2021·南通崇川区月考] 如图,在△ABC中,D,E两点分别在BC,AC上,且AD平分
∠BAC,若∠ABE=∠C,BE与AD相交于点F,则图中相似三角形的对数是 ( )
A.1 B.2 C.3 D.4
图 4.[教材练习第2题变式] [2020·昆山期末] 如图,DE∥BC.若EC=3EA,则AB= ,BC= .
5.[2021·淮安期末] 如图,在矩形ABCD中,E为AD上一点,EF⊥EC交AB于点F,连接FC.求证:△AEF∽△DCE.
6.如图,在△ABC中,∠ABC=80°,∠A=40°,AB的垂直平分线DE分别交AC,AB于点D,E,连接BD.求证:△ABC∽△BDC.
知识点 2 判定两个三角形相似的运用
7.如图,在矩形ABCD中,AB=2,BC=3.若E是边CD的中点,连接AE,过点B作BF⊥AE于点F,则BF的长为 ( )
A. B. C. D.
8.如图,在△ABC中,D为AB边上一点,且∠BCD=∠A.已知BC=2,AB=3,则BD= .
9.已知:如图,在△ABC中,D,E分别是AB,AC上的点,且∠AED=∠B.若AE=5,AB=9,CB=6,求DE的长.
10.[2020·常州期末] 如图,在△ABC中,AC=4,D是AC上一点,AD=1,若∠ABD=∠ACB,则的值是 ( )
A. B. C. D.
11.如图,在△ADE中,AD=AE,C为DE延长线上一点,B为ED延长线上一点,∠DAE=40°,则当∠BAC= °时,△BDA∽△AEC.
12.[2021·淮安淮安区期末] 如图,在△ABC中,D是BC上一点,∠DAC=∠B,E为AB上一点.
(1)求证:△CAD∽△CBA;
(2)若BD=10,DC=8,求AC的长;
(3)在(2)的条件下,若DE∥AC,AE=4,求BE的长.
13.如图,在☉O中,弦AB,CD相交于点P.求证:PA·PB=PC·PD.
14.[2020·南京期末] 如图,在等边三角形ABC中,P为BC上一点,D为AC上一点,且
∠APD=60°,2BP=3CD,BP=1.
(1)求证:△ABP∽△PCD;
(2)求△ABC的边长.
15.[2020·南京玄武区期末] 如图,在△ABC中,AB=3,AC=4,BC=6,D是BC上一点,CD=2,过点D的直线l将△ABC分成两部分,使其所分成的三角形与△ABC相似,若直线l与△ABC另一边的交点为P,则DP的长为 .
答案
第2课时 利用两角证相似
1.B
2.C ∵∠1=∠2,∠A=∠A,
∴△ADE∽△ABC.
∵∠1=∠3,∠A=∠A,
∴△ADE∽△ACD.
∵∠2=∠3,∠A=∠A,
∴△ABC∽△ACD.
无法判定△ADE∽△EDC.故选C.
3.C 如图,①在△ABE与△ACB中,∠ABE=∠C,∠BAE=∠CAB,则△ABE∽△ACB;
②∵AD平分∠BAC,∴∠1=∠2.又∵∠ABF=∠C,∴△ABF∽△ACD;
③∵△ABE∽△ACB,∴∠BEA=∠ABD.
又∵∠1=∠2,∴△AEF∽△ABD,综合①②③知,共有3对相似三角形.故选C.
4.20 24 由EC=3EA,得AC=2AE.∵DE∥BC,∴∠D=∠B,∠E=∠C,∴△AED∽
△ACB,∴===,即==,∴AB=20,BC=24.
5.证明:∵∠FEC=90°,
∴∠AEF+∠DEC=90°.
∵四边形ABCD是矩形,∴∠A=∠D=90°.
∵∠A+∠AFE+∠AEF=180°,
∴∠AFE+∠AEF=90°,
∴∠DEC=∠AFE.
又∵∠A=∠D,∴△AEF∽△DCE.
6.证明:∵DE是AB的垂直平分线,
∴AD=BD,
∴∠ABD=∠A=40°.
∵∠ABC=80°,
∴∠DBC=40°,
∴∠A=∠DBC.
又∵∠C=∠C,
∴△ABC∽△BDC.
7.B 在矩形ABCD中,∵E是边CD的中点,CD=AB=2,∴DE=1.
在Rt△ADE中,AE==.∵BF⊥AE,∴∠AFB=∠D=90°.
∵∠DAE+∠BAE=90°,∠FBA+∠BAE=90°,∴∠DAE=∠FBA,∴△ADE∽△BFA,从而=,∴=,∴BF=.
8. ∵∠BCD=∠A,∠B=∠B,
∴△DCB∽△CAB,∴=,
∴=,∴BD=.
9.解:∵∠AED=∠B,∠A=∠A,
∴△AED∽△ABC,
∴=.
∵AE=5,AB=9,CB=6,
∴=,解得DE=.
10.C ∵∠ABD=∠ACB,∠BAD=∠CAB,∴△ABD∽△ACB,∴=,∴=,
∴AB=2(负值已舍去),∴=.故选C.
11.110 ∵AD=AE,∠DAE=40°,
∴∠ADE=∠AED=70°,
∴∠B+∠BAD=70°.
∵△BDA∽△AEC,
∴∠B=∠EAC,
∴∠EAC+∠BAD=∠B+∠BAD=70°,
∴∠BAC=(∠EAC+∠BAD)+∠DAE=70°+40°=110°.故答案为110.
12.解:(1)证明:∵∠DAC=∠B,∠C=∠C,
∴△CAD∽△CBA.
(2)∵△CAD∽△CBA,
∴=,
∴=,∴AC=12(负值已舍去).
(3)∵DE∥AC,∴=,
即=,∴BE=5.
13.证明:如图,连接AC,BD,则∠CAB=∠BDC.
又∵∠APC=∠DPB,
∴△APC∽△DPB,
∴=,
∴PA·PB=PC·PD.
14.解:(1)证明:∵△ABC是等边三角形,
∴∠B=∠C=60°.
∵∠BPA+∠APD+∠DPC=180°,且∠APD=60°,
∴∠BPA+∠DPC=120°.
∵∠DPC+∠C+∠CDP=180°,
∴∠DPC+∠CDP=120°,∴∠BPA=∠CDP,∴△ABP∽△PCD.
(2)∵2BP=3CD,且BP=1,∴CD=.
∵△ABP∽△PCD,∴=.
设AB=x,则PC=x-1,∴=,∴x=3,即AB=3,∴△ABC的边长为3.
15.1或或 如图①,若DP∥AB,
则△CDP∽△CBA,
∴=,
即=,∴DP=1.
如图②,若DP∥AC,
则△BDP∽△BCA,
∴=,
即=,
∴PD=.
如图③,若∠CDP=∠A,
∵∠C=∠C,
∴△CDP∽△CAB,
∴=,
即=,
∴PD=.
综上所述,DP的长为1或或.
故答案为1或或.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
