苏科版数学九年级下册 6.4 第5课时 圆中的相似、三角形的重心 同步课时练习(word版 含解析)
文档属性
| 名称 | 苏科版数学九年级下册 6.4 第5课时 圆中的相似、三角形的重心 同步课时练习(word版 含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 313.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-15 06:51:01 | ||
图片预览



文档简介
第5课时 圆中的相似、三角形的重心
知识点 1 圆中的相似
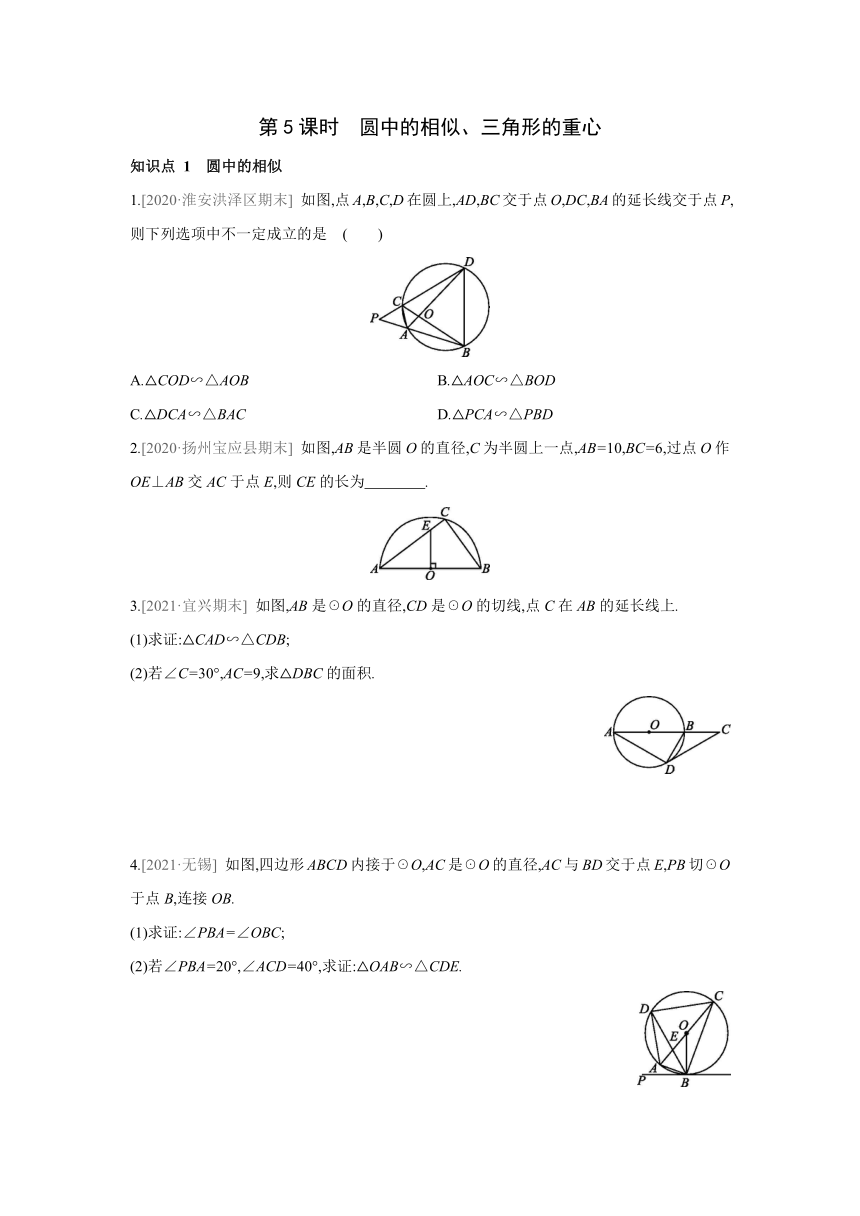
1.[2020·淮安洪泽区期末] 如图,点A,B,C,D在圆上,AD,BC交于点O,DC,BA的延长线交于点P,则下列选项中不一定成立的是 ( )
A.△COD∽△AOB B.△AOC∽△BOD
C.△DCA∽△BAC D.△PCA∽△PBD
2.[2020·扬州宝应县期末] 如图,AB是半圆O的直径,C为半圆上一点,AB=10,BC=6,过点O作OE⊥AB交AC于点E,则CE的长为 .
3.[2021·宜兴期末] 如图,AB是☉O的直径,CD是☉O的切线,点C在AB的延长线上.
(1)求证:△CAD∽△CDB;
(2)若∠C=30°,AC=9,求△DBC的面积.
4.[2021·无锡] 如图,四边形ABCD内接于☉O,AC是☉O的直径,AC与BD交于点E,PB切☉O于点B,连接OB.
(1)求证:∠PBA=∠OBC;
(2)若∠PBA=20°,∠ACD=40°,求证:△OAB∽△CDE.
知识点 2 三角形的重心
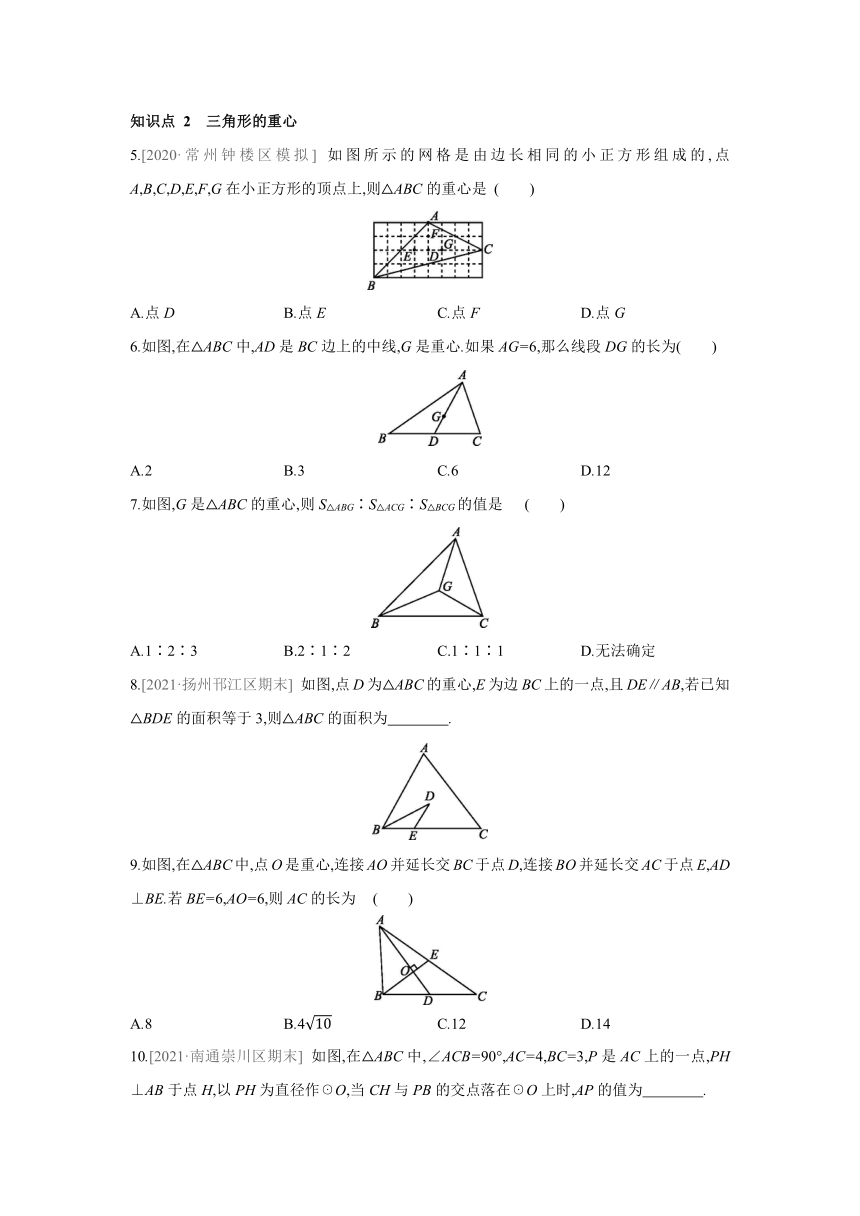
5.[2020·常州钟楼区模拟] 如图所示的网格是由边长相同的小正方形组成的,点A,B,C,D,E,F,G在小正方形的顶点上,则△ABC的重心是 ( )
A.点D B.点E C.点F D.点G
6.如图,在△ABC中,AD是BC边上的中线,G是重心.如果AG=6,那么线段DG的长为( )
A.2 B.3 C.6 D.12
7.如图,G是△ABC的重心,则S△ABG∶S△ACG∶S△BCG的值是 ( )
A.1∶2∶3 B.2∶1∶2 C.1∶1∶1 D.无法确定
8.[2021·扬州邗江区期末] 如图,点D为△ABC的重心,E为边BC上的一点,且DE∥AB,若已知△BDE的面积等于3,则△ABC的面积为 .
9.如图,在△ABC中,点O是重心,连接AO并延长交BC于点D,连接BO并延长交AC于点E,AD⊥BE.若BE=6,AO=6,则AC的长为 ( )
A.8 B.4 C.12 D.14
10.[2021·南通崇川区期末] 如图,在△ABC中,∠ACB=90°,AC=4,BC=3,P是AC上的一点,PH⊥AB于点H,以PH为直径作☉O,当CH与PB的交点落在☉O上时,AP的值为 .
11.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AD=18,点E在AC上且CE=AC,连接BE,与AD交于点F.若BE=15,则△DBF的周长是 .
12.[2020·南京六合区期末] 如图,AC与☉O交于B,C两点,AD过圆心O且与☉O交于E,D两点,OB平分∠AOC.
(1)求证:△ACD∽△ABO;
(2)过点E作☉O的切线交AC于点F,若EF∥OC,OC=3,求EF的长.
13.如图,已知G是△ABC的重心,AG⊥GC.
(1)若AC=4 cm,求BG的长;
(2)若△ABC的面积为9 cm2,求△GBC的面积.
14.如图,已知四边形ABCD是矩形,DE∥AC,交BC的延长线于点E,AE交CD于点F,BF交AC于点G.
(1)求证:G是△ABE的重心;
(2)已知=,求证:∠BCG=∠BGC.
答案
第5课时 圆中的相似、三角形的重心
1.C ∵∠OCD=∠OAB,∠COD=∠AOB,∴△COD∽△AOB.同理可证:△AOC∽
△BOD.∵∠PCA+∠ACD=180°,∠ACD+∠PBD=180°,∴∠PCA=∠PBD.又∵∠P=∠P,
∴△PCA∽△PBD.无法证得△DCA∽△BAC.故选C.
2. ∵AB是半圆O的直径,
∴∠ACB=90°.
在Rt△ABC中,由勾股定理得AC==8.
∵OE⊥AB,∴∠AOE=∠ACB=90°.
又∵∠OAE=∠CAB,
∴△AOE∽△ACB,
∴=,即=,
解得AE=,
∴CE=AC-AE=.
3.解:(1)证明:如图,连接OD.
∵OB=OD,∴∠ODB=∠ABD.
∵CD是☉O的切线,∴∠ODC=90°,
∴∠ODB+∠CDB=90°.
∵AB是☉O的直径,∴∠ADB=90°,
∴∠ABD+∠BAD=90°,
∴∠CAD=∠CDB.
又∵∠C=∠C,∴△CAD∽△CDB.
(2)∵∠ODC=90°,∠C=30°,∴OC=2OD.
∵AB是☉O的直径,AC=9,
∴OA=OB=OD=BC=AC=3.
由(1)得△CAD∽△CDB,
∴CD∶CB=CA∶CD,
∴CD2=CB·CA=3×9=27,
∴CD==3,
∴△OCD的面积=OD·CD=×3×3=.
又∵BC=OB,
∴△DBC的面积=×△OCD的面积=.
4.证明:(1)∵AC是☉O的直径,
∴∠ABC=90°,
∴∠ABO+∠OBC=90°.
∵PB切☉O于点B,∴∠OBP=90°,
∴∠PBA+∠ABO=90°,
∴∠PBA=∠OBC.
(2)∵OB=OC,∴∠ACB=∠OBC,
∴∠PBA=∠OBC=∠ACB.
∵∠PBA=20°,∴∠OBC=∠ACB=20°,
∴∠AOB=∠ACB+∠OBC=20°+20°=40°.
∵∠ACD=40°,∴∠AOB=∠ACD.
∵同弧所对的圆周角相等,∴∠CDB=∠BAC,即∠OAB=∠CDE,∴△OAB∽△CDE.
5.A 如图,分别作AB,BC边上的中线,交于点D,则点D是△ABC的重心.故选A.
6.B 根据重心的性质,三角形的重心到一顶点的距离等于其到对边中点距离的2倍,可直接求得结果.
7.C 如图,延长AG交BC于点D.
∵G为△ABC的重心,∴D是BC边的中点,
∴S△ABD=S△ACD,S△BDG=S△CDG,
∴S△ABG=S△ACG.
同理可证S△ABG=S△BCG,
∴S△ABG∶S△ACG∶S△BCG=1∶1∶1.
故选C.
8.27 连接AD,并延长交BC于点F,连接AE,如图.
∵DE∥AB,∴S△ADE=S△BDE=3.
∵点D为△ABC的重心,∴AD=2DF,
∴S△DEF=S△ADE=1.5,
∴S△BDF=1.5+3=4.5,
∴S△ABD=2S△BDF=9,
∴S△ABF=4.5+9=13.5.
∵AF为△ABC的中线,
∴S△ABC=2S△ABF=2×13.5=27.
9.B ∵O是△ABC的重心,
∴E是AC的中点,OE=BE=×6=2.
∵AD⊥BE,∴AE==2,
∴AC=2AE=2×2=4.
故选B.
10. 如图所示.
∵HP是☉O的直径,∴∠HDP=90°,
∴∠HDP=∠BDH=90°.
∵∠PHD+∠BHD=90°,∠BHD+∠HBD=90°,
∴∠PHD=∠HBD,∴△PHD∽△HBD,
∴=,∴HD2=PD·BD.
同理可证CD2=PD·BD,
∴HD=CD,∴BD垂直平分CH,
∴BH=BC=3.
在Rt△ACB中,AB==5,
∴AH=5-3=2.
∵∠A=∠A,∠AHP=∠ACB=90°,
∴△AHP∽△ACB,∴=,即=,
∴AP=.
11.24 根据等腰三角形三线合一的性质得出BD=CD,又由CE=AC,可知F是△ABC的重心,根据重心的性质,得BF=BE=10,DF=AD=6.在Rt△BDF中利用勾股定理求得BD=8,进而得出△DBF的周长为24.
12.解:(1)证明:∵OB平分∠AOC,
∴∠BOE=∠AOC.
由圆周角定理可得∠D=∠AOC,
∴∠D=∠BOE.
又∵∠A=∠A,
∴△ACD∽△ABO.
(2)∵EF切☉O于点E,
∴∠OEF=90°.
∵EF∥OC,∴∠DOC=∠OEF=90°.
∵OC=OD=3,
∴CD==3.
∵△ACD∽△ABO,
∴=,即=,
∴AE=3.
∵EF∥OC,∴△AEF∽△AOC,
∴=,
即=,
∴EF=6-3.
13.解:(1)如图,延长BG交AC于点D.
∵G是△ABC的重心,
∴BG=2GD,BD为△ABC的中线.
又∵AG⊥GC,
∴GD为Rt△AGC斜边上的中线,
∴GD=AC,
∴BG=2GD=AC=4 cm.
(2)∵BD为△ABC的中线,
∴S△CBD=S△ABC= cm2.
∵BG=2GD,
∴S△GBC=S△CBD=3 cm2.
14.证明:(1)∵四边形ABCD是矩形,
∴AD∥BE,AD=BC.
又∵DE∥AC,
∴四边形ACED是平行四边形,
∴AF=EF,AD=CE.
∵AD=BC,∴BC=CE,
∴G是△ABE的重心.
(2)∵∠ABE=90°,AF=EF,
∴BF=AE=AF.
∵G是△ABE的重心,
∴BG=BF=AF.
∵=,∴BC=AD=AF,
∴BC=BG,
∴∠BCG=∠BGC.
知识点 1 圆中的相似
1.[2020·淮安洪泽区期末] 如图,点A,B,C,D在圆上,AD,BC交于点O,DC,BA的延长线交于点P,则下列选项中不一定成立的是 ( )
A.△COD∽△AOB B.△AOC∽△BOD
C.△DCA∽△BAC D.△PCA∽△PBD
2.[2020·扬州宝应县期末] 如图,AB是半圆O的直径,C为半圆上一点,AB=10,BC=6,过点O作OE⊥AB交AC于点E,则CE的长为 .
3.[2021·宜兴期末] 如图,AB是☉O的直径,CD是☉O的切线,点C在AB的延长线上.
(1)求证:△CAD∽△CDB;
(2)若∠C=30°,AC=9,求△DBC的面积.
4.[2021·无锡] 如图,四边形ABCD内接于☉O,AC是☉O的直径,AC与BD交于点E,PB切☉O于点B,连接OB.
(1)求证:∠PBA=∠OBC;
(2)若∠PBA=20°,∠ACD=40°,求证:△OAB∽△CDE.
知识点 2 三角形的重心
5.[2020·常州钟楼区模拟] 如图所示的网格是由边长相同的小正方形组成的,点A,B,C,D,E,F,G在小正方形的顶点上,则△ABC的重心是 ( )
A.点D B.点E C.点F D.点G
6.如图,在△ABC中,AD是BC边上的中线,G是重心.如果AG=6,那么线段DG的长为( )
A.2 B.3 C.6 D.12
7.如图,G是△ABC的重心,则S△ABG∶S△ACG∶S△BCG的值是 ( )
A.1∶2∶3 B.2∶1∶2 C.1∶1∶1 D.无法确定
8.[2021·扬州邗江区期末] 如图,点D为△ABC的重心,E为边BC上的一点,且DE∥AB,若已知△BDE的面积等于3,则△ABC的面积为 .
9.如图,在△ABC中,点O是重心,连接AO并延长交BC于点D,连接BO并延长交AC于点E,AD⊥BE.若BE=6,AO=6,则AC的长为 ( )
A.8 B.4 C.12 D.14
10.[2021·南通崇川区期末] 如图,在△ABC中,∠ACB=90°,AC=4,BC=3,P是AC上的一点,PH⊥AB于点H,以PH为直径作☉O,当CH与PB的交点落在☉O上时,AP的值为 .
11.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AD=18,点E在AC上且CE=AC,连接BE,与AD交于点F.若BE=15,则△DBF的周长是 .
12.[2020·南京六合区期末] 如图,AC与☉O交于B,C两点,AD过圆心O且与☉O交于E,D两点,OB平分∠AOC.
(1)求证:△ACD∽△ABO;
(2)过点E作☉O的切线交AC于点F,若EF∥OC,OC=3,求EF的长.
13.如图,已知G是△ABC的重心,AG⊥GC.
(1)若AC=4 cm,求BG的长;
(2)若△ABC的面积为9 cm2,求△GBC的面积.
14.如图,已知四边形ABCD是矩形,DE∥AC,交BC的延长线于点E,AE交CD于点F,BF交AC于点G.
(1)求证:G是△ABE的重心;
(2)已知=,求证:∠BCG=∠BGC.
答案
第5课时 圆中的相似、三角形的重心
1.C ∵∠OCD=∠OAB,∠COD=∠AOB,∴△COD∽△AOB.同理可证:△AOC∽
△BOD.∵∠PCA+∠ACD=180°,∠ACD+∠PBD=180°,∴∠PCA=∠PBD.又∵∠P=∠P,
∴△PCA∽△PBD.无法证得△DCA∽△BAC.故选C.
2. ∵AB是半圆O的直径,
∴∠ACB=90°.
在Rt△ABC中,由勾股定理得AC==8.
∵OE⊥AB,∴∠AOE=∠ACB=90°.
又∵∠OAE=∠CAB,
∴△AOE∽△ACB,
∴=,即=,
解得AE=,
∴CE=AC-AE=.
3.解:(1)证明:如图,连接OD.
∵OB=OD,∴∠ODB=∠ABD.
∵CD是☉O的切线,∴∠ODC=90°,
∴∠ODB+∠CDB=90°.
∵AB是☉O的直径,∴∠ADB=90°,
∴∠ABD+∠BAD=90°,
∴∠CAD=∠CDB.
又∵∠C=∠C,∴△CAD∽△CDB.
(2)∵∠ODC=90°,∠C=30°,∴OC=2OD.
∵AB是☉O的直径,AC=9,
∴OA=OB=OD=BC=AC=3.
由(1)得△CAD∽△CDB,
∴CD∶CB=CA∶CD,
∴CD2=CB·CA=3×9=27,
∴CD==3,
∴△OCD的面积=OD·CD=×3×3=.
又∵BC=OB,
∴△DBC的面积=×△OCD的面积=.
4.证明:(1)∵AC是☉O的直径,
∴∠ABC=90°,
∴∠ABO+∠OBC=90°.
∵PB切☉O于点B,∴∠OBP=90°,
∴∠PBA+∠ABO=90°,
∴∠PBA=∠OBC.
(2)∵OB=OC,∴∠ACB=∠OBC,
∴∠PBA=∠OBC=∠ACB.
∵∠PBA=20°,∴∠OBC=∠ACB=20°,
∴∠AOB=∠ACB+∠OBC=20°+20°=40°.
∵∠ACD=40°,∴∠AOB=∠ACD.
∵同弧所对的圆周角相等,∴∠CDB=∠BAC,即∠OAB=∠CDE,∴△OAB∽△CDE.
5.A 如图,分别作AB,BC边上的中线,交于点D,则点D是△ABC的重心.故选A.
6.B 根据重心的性质,三角形的重心到一顶点的距离等于其到对边中点距离的2倍,可直接求得结果.
7.C 如图,延长AG交BC于点D.
∵G为△ABC的重心,∴D是BC边的中点,
∴S△ABD=S△ACD,S△BDG=S△CDG,
∴S△ABG=S△ACG.
同理可证S△ABG=S△BCG,
∴S△ABG∶S△ACG∶S△BCG=1∶1∶1.
故选C.
8.27 连接AD,并延长交BC于点F,连接AE,如图.
∵DE∥AB,∴S△ADE=S△BDE=3.
∵点D为△ABC的重心,∴AD=2DF,
∴S△DEF=S△ADE=1.5,
∴S△BDF=1.5+3=4.5,
∴S△ABD=2S△BDF=9,
∴S△ABF=4.5+9=13.5.
∵AF为△ABC的中线,
∴S△ABC=2S△ABF=2×13.5=27.
9.B ∵O是△ABC的重心,
∴E是AC的中点,OE=BE=×6=2.
∵AD⊥BE,∴AE==2,
∴AC=2AE=2×2=4.
故选B.
10. 如图所示.
∵HP是☉O的直径,∴∠HDP=90°,
∴∠HDP=∠BDH=90°.
∵∠PHD+∠BHD=90°,∠BHD+∠HBD=90°,
∴∠PHD=∠HBD,∴△PHD∽△HBD,
∴=,∴HD2=PD·BD.
同理可证CD2=PD·BD,
∴HD=CD,∴BD垂直平分CH,
∴BH=BC=3.
在Rt△ACB中,AB==5,
∴AH=5-3=2.
∵∠A=∠A,∠AHP=∠ACB=90°,
∴△AHP∽△ACB,∴=,即=,
∴AP=.
11.24 根据等腰三角形三线合一的性质得出BD=CD,又由CE=AC,可知F是△ABC的重心,根据重心的性质,得BF=BE=10,DF=AD=6.在Rt△BDF中利用勾股定理求得BD=8,进而得出△DBF的周长为24.
12.解:(1)证明:∵OB平分∠AOC,
∴∠BOE=∠AOC.
由圆周角定理可得∠D=∠AOC,
∴∠D=∠BOE.
又∵∠A=∠A,
∴△ACD∽△ABO.
(2)∵EF切☉O于点E,
∴∠OEF=90°.
∵EF∥OC,∴∠DOC=∠OEF=90°.
∵OC=OD=3,
∴CD==3.
∵△ACD∽△ABO,
∴=,即=,
∴AE=3.
∵EF∥OC,∴△AEF∽△AOC,
∴=,
即=,
∴EF=6-3.
13.解:(1)如图,延长BG交AC于点D.
∵G是△ABC的重心,
∴BG=2GD,BD为△ABC的中线.
又∵AG⊥GC,
∴GD为Rt△AGC斜边上的中线,
∴GD=AC,
∴BG=2GD=AC=4 cm.
(2)∵BD为△ABC的中线,
∴S△CBD=S△ABC= cm2.
∵BG=2GD,
∴S△GBC=S△CBD=3 cm2.
14.证明:(1)∵四边形ABCD是矩形,
∴AD∥BE,AD=BC.
又∵DE∥AC,
∴四边形ACED是平行四边形,
∴AF=EF,AD=CE.
∵AD=BC,∴BC=CE,
∴G是△ABE的重心.
(2)∵∠ABE=90°,AF=EF,
∴BF=AE=AF.
∵G是△ABE的重心,
∴BG=BF=AF.
∵=,∴BC=AD=AF,
∴BC=BG,
∴∠BCG=∠BGC.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
