苏科版数学九年级下册 7.1 正切 同步课时练习(word版 含解析)
文档属性
| 名称 | 苏科版数学九年级下册 7.1 正切 同步课时练习(word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 246.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-15 06:53:40 | ||
图片预览


文档简介
7.1 正切
知识点 1 正切的概念
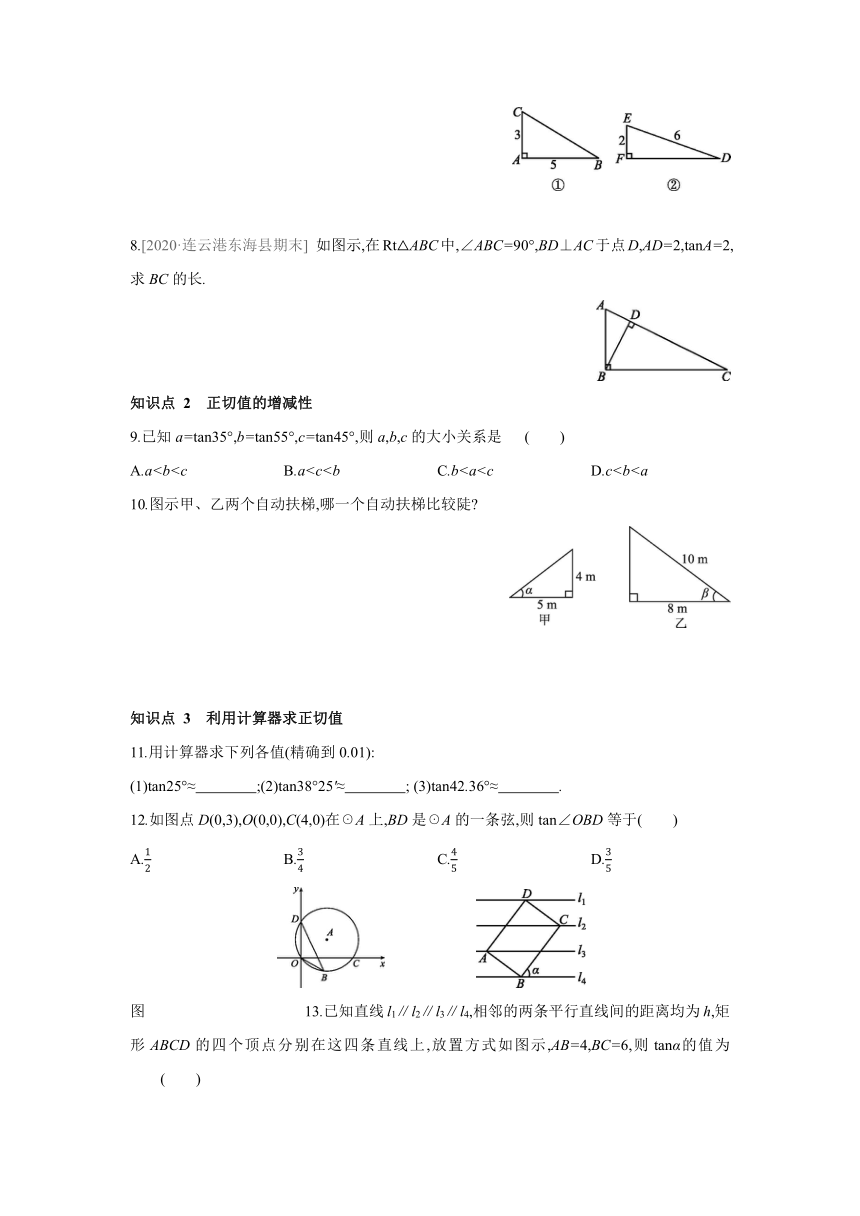
1.如图在Rt△ABC中,∠C=90°,AC=24,BC=7,求tanA的值.
解:在Rt△ABC中,∠C=90°,
∵∠A的对边是 ,∠A的邻边是 ,∴tanA== .
2.[2020·泰州高港区模拟] 如图在由边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tanA的值为 ( )
A. B. C. D.
3.[2021·无锡惠山区期中] 在Rt△ABC中,各边都扩大为原来的5倍,则锐角A的正切值( )
A.不变 B.扩大为原来的5倍
C.缩小为原来的 D.不能确定
4.[2021·江阴期末] 在△ABC中,∠C=90°,AB=13 cm,BC=5 cm,则tanB= .
5.[2020·常州天宁区模拟] 如图点P(12,a)在反比例函数y=(x>0)的图像上,PH⊥x轴于点H,则tan∠POH的值为 .
6.在Rt△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边,若tanA=,c=2,则b的值等于 .
7.分别求图②中各直角三角形锐角的正切值.
8.[2020·连云港东海县期末] 如图示,在Rt△ABC中,∠ABC=90°,BD⊥AC于点D,AD=2,tanA=2,求BC的长.
知识点 2 正切值的增减性
9.已知a=tan35°,b=tan55°,c=tan45°,则a,b,c的大小关系是 ( )
A.a10.图示甲、乙两个自动扶梯,哪一个自动扶梯比较陡
知识点 3 利用计算器求正切值
11.用计算器求下列各值(精确到0.01):
(1)tan25°≈ ;(2)tan38°25'≈ ; (3)tan42.36°≈ .
12.如图点D(0,3),O(0,0),C(4,0)在☉A上,BD是☉A的一条弦,则tan∠OBD等于( )
A. B. C. D.
图 13.已知直线l1∥l2∥l3∥l4,相邻的两条平行直线间的距离均为h,矩形ABCD的四个顶点分别在这四条直线上,放置方式如图示,AB=4,BC=6,则tanα的值为 ( )
A. B. C. D.
14.[2020·常州] 如图点C在线段AB上,且AC=2BC,分别以AC,BC为边在线段AB的同侧作正方形ACDE,BCFG,连接EC,EG,则tan∠CEG= .
15.[2020·苏州相城区期末] 如图,在Rt△ABC中,∠ACB=90°,tanA=,点D,E分别在边AB,AC上,DE⊥AC,DE=3,DB=10.求CD的长.
16.如图,△ABC表示一块三角形的草地,其中BC=10 m, tanB=2,tanC=.试求这块三角形草地的面积.
17.[2020·江阴模拟] 如图,将含30°角的三角尺ABC(∠A=30°)绕其直角顶点C顺时针旋转α(0°<α<90°),得到Rt△A'B'C,A'C与AB交于点D,过点D作DE∥A'B'交CB'于点E,连接BE.易知,在旋转过程中,△BDE为直角三角形.设BC=1,AD=x,△BDE的面积为S.
(1)求S与x之间的函数表达式,并写出x的取值范围;
(2)以点E为圆心,BE为半径作☉E,当S=S△ABC时,判断☉E与A'C的位置关系,并求出相应的tanα的值.
答案
7.1 正切
1.BC AC BC AC 2.D
3.A 锐角三角函数值随着角度的变化而变化,而角的大小与边的长短没有关系,因此锐角A的正切值不变.故选A.
4. 由勾股定理,得AC===12,
∴tanB==.
5. ∵点P(12,a)在反比例函数y=的图像上,∴a==5.∵PH⊥x轴于点H,
∴PH=5,OH=12,∴tan∠POH=.
6. 在Rt△ABC中,∠C=90°,tanA=,则=,∴b=2a.
在Rt△ABC中,由勾股定理,得a2+b2=c2,即a2+(2a)2=22,
解得a=(负值已舍去),∴b=2a=.
7.解:图①中,tanB=,tanC=;
图②中,tanD=,tanE=2.
8.解:在Rt△ABD中,tanA==2,AD=2,
∴BD=4,
∴AB===2.
在Rt△ABC中,tanA==2,
∴BC=4.
9.B 可用计算器分别求出a,b,c的值,再比较大小;也可根据正切值的变化趋势进行大小比较,即由55°>45°>35°,得tan55°>tan45°>tan35°,故a10. 比较两个扶梯的倾斜程度,可转化为比较这两个扶梯与地面的夹角α,β的正切值,锐角的正切值越大,扶梯就越陡.
解:甲图中:tanα=;
乙图中:由勾股定理先求出锐角β的对边长为=6,
∴tanβ==.
∵>,
∴自动扶梯甲比较陡.
11.(1)0.47 (2)0.79 (3)0.91
12.B ∵D(0,3),C(4,0),
∴OD=3,OC=4.
连接CD,如图所示.
易得∠OBD=∠OCD,
∴tan∠OBD=tan∠OCD==.
故选B.
13.C 如图,过点C作CE⊥l4于点E,延长EC交l1于点F.
∵∠α+∠BCE=90°,
∠BCE+∠DCF=180°-90°=90°,
∴∠α=∠DCF.
又∵∠BEC=∠CFD=90°,
∴△BEC∽△CFD,
∴BE∶CF=BC∶CD,
即=,∴BE=.
在Rt△BCE中,∵∠BEC=90°,
∴tanα===.
14. 连接CG.∵四边形ACDE,BCFG是正方形.
∴∠ECG=45°+45°=90°.
设BC=a,则AC=2a,CG=a,∴CE=2a,∴tan∠CEG===.
15.解:∵DE⊥AC,∴∠DEA=90°.
在Rt△ADE中,tanA==.
∵DE=3,∴AE=4,
∴AD==5,
∴AB=BD+AD=10+5=15.
在Rt△ABC中,tanA==,
设BC=3x,则AC=4x,∴AB=5x,
即5x=15,解得x=3.
∴AC=4x=12,
∴CE=AC-AE=12-4=8.
在Rt△CDE中,CD===.
16.解:如图,过点A作AD⊥BC于点D.
在Rt△ABD中,tanB==2.
在Rt△ACD中,tanC==.
设AD=x m,则BD=x m,CD=2x m.
∵BC=10 m,
∴x+2x=10,解得x=4.
故这块三角形草地的面积为AD·BC=×4×10=20(m2).
17.解:(1)由题意,得∠DBE=90°,∠ABC=60°,
∴∠A=∠CBE=30°.
又∵∠ACB=90°,BC=1,
∴AC=BC=,AB=2BC=2.
由旋转性质可知AC=A'C,BC=B'C,∠ACD=∠BCE,
从而△ADC∽△BEC,
∴=,即=,∴BE=x.
由上易得BD=2-x,
∴S=BE·BD=×x·(2-x)=-x2+x(0(2)∵S=S△ABC,
∴-x2+x=××1×,
∴4x2-8x+3=0,∴x1=,x2=.
①当x=时,BD=2-=,BE=×=,
∴DE==.
∵DE∥A'B',∴∠EDC=∠A'=∠A=30°.
又∵∠A'CB'=90°,
∴EC=DE=>BE,
∴此时☉E与A'C相离.
过点D作DF⊥AC于点F,如图.
则DF=x=,AF=DF=,
∴CF=AC-AF=-= ,
∴tanα===.
②当x=时,BD=AB-AD=2-=,BE=×=,
∴DE==1,
同理可求EC=DE=∴此时☉E与A'C相交.
同理可求出tanα=.
知识点 1 正切的概念
1.如图在Rt△ABC中,∠C=90°,AC=24,BC=7,求tanA的值.
解:在Rt△ABC中,∠C=90°,
∵∠A的对边是 ,∠A的邻边是 ,∴tanA== .
2.[2020·泰州高港区模拟] 如图在由边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tanA的值为 ( )
A. B. C. D.
3.[2021·无锡惠山区期中] 在Rt△ABC中,各边都扩大为原来的5倍,则锐角A的正切值( )
A.不变 B.扩大为原来的5倍
C.缩小为原来的 D.不能确定
4.[2021·江阴期末] 在△ABC中,∠C=90°,AB=13 cm,BC=5 cm,则tanB= .
5.[2020·常州天宁区模拟] 如图点P(12,a)在反比例函数y=(x>0)的图像上,PH⊥x轴于点H,则tan∠POH的值为 .
6.在Rt△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边,若tanA=,c=2,则b的值等于 .
7.分别求图②中各直角三角形锐角的正切值.
8.[2020·连云港东海县期末] 如图示,在Rt△ABC中,∠ABC=90°,BD⊥AC于点D,AD=2,tanA=2,求BC的长.
知识点 2 正切值的增减性
9.已知a=tan35°,b=tan55°,c=tan45°,则a,b,c的大小关系是 ( )
A.a
知识点 3 利用计算器求正切值
11.用计算器求下列各值(精确到0.01):
(1)tan25°≈ ;(2)tan38°25'≈ ; (3)tan42.36°≈ .
12.如图点D(0,3),O(0,0),C(4,0)在☉A上,BD是☉A的一条弦,则tan∠OBD等于( )
A. B. C. D.
图 13.已知直线l1∥l2∥l3∥l4,相邻的两条平行直线间的距离均为h,矩形ABCD的四个顶点分别在这四条直线上,放置方式如图示,AB=4,BC=6,则tanα的值为 ( )
A. B. C. D.
14.[2020·常州] 如图点C在线段AB上,且AC=2BC,分别以AC,BC为边在线段AB的同侧作正方形ACDE,BCFG,连接EC,EG,则tan∠CEG= .
15.[2020·苏州相城区期末] 如图,在Rt△ABC中,∠ACB=90°,tanA=,点D,E分别在边AB,AC上,DE⊥AC,DE=3,DB=10.求CD的长.
16.如图,△ABC表示一块三角形的草地,其中BC=10 m, tanB=2,tanC=.试求这块三角形草地的面积.
17.[2020·江阴模拟] 如图,将含30°角的三角尺ABC(∠A=30°)绕其直角顶点C顺时针旋转α(0°<α<90°),得到Rt△A'B'C,A'C与AB交于点D,过点D作DE∥A'B'交CB'于点E,连接BE.易知,在旋转过程中,△BDE为直角三角形.设BC=1,AD=x,△BDE的面积为S.
(1)求S与x之间的函数表达式,并写出x的取值范围;
(2)以点E为圆心,BE为半径作☉E,当S=S△ABC时,判断☉E与A'C的位置关系,并求出相应的tanα的值.
答案
7.1 正切
1.BC AC BC AC 2.D
3.A 锐角三角函数值随着角度的变化而变化,而角的大小与边的长短没有关系,因此锐角A的正切值不变.故选A.
4. 由勾股定理,得AC===12,
∴tanB==.
5. ∵点P(12,a)在反比例函数y=的图像上,∴a==5.∵PH⊥x轴于点H,
∴PH=5,OH=12,∴tan∠POH=.
6. 在Rt△ABC中,∠C=90°,tanA=,则=,∴b=2a.
在Rt△ABC中,由勾股定理,得a2+b2=c2,即a2+(2a)2=22,
解得a=(负值已舍去),∴b=2a=.
7.解:图①中,tanB=,tanC=;
图②中,tanD=,tanE=2.
8.解:在Rt△ABD中,tanA==2,AD=2,
∴BD=4,
∴AB===2.
在Rt△ABC中,tanA==2,
∴BC=4.
9.B 可用计算器分别求出a,b,c的值,再比较大小;也可根据正切值的变化趋势进行大小比较,即由55°>45°>35°,得tan55°>tan45°>tan35°,故a
解:甲图中:tanα=;
乙图中:由勾股定理先求出锐角β的对边长为=6,
∴tanβ==.
∵>,
∴自动扶梯甲比较陡.
11.(1)0.47 (2)0.79 (3)0.91
12.B ∵D(0,3),C(4,0),
∴OD=3,OC=4.
连接CD,如图所示.
易得∠OBD=∠OCD,
∴tan∠OBD=tan∠OCD==.
故选B.
13.C 如图,过点C作CE⊥l4于点E,延长EC交l1于点F.
∵∠α+∠BCE=90°,
∠BCE+∠DCF=180°-90°=90°,
∴∠α=∠DCF.
又∵∠BEC=∠CFD=90°,
∴△BEC∽△CFD,
∴BE∶CF=BC∶CD,
即=,∴BE=.
在Rt△BCE中,∵∠BEC=90°,
∴tanα===.
14. 连接CG.∵四边形ACDE,BCFG是正方形.
∴∠ECG=45°+45°=90°.
设BC=a,则AC=2a,CG=a,∴CE=2a,∴tan∠CEG===.
15.解:∵DE⊥AC,∴∠DEA=90°.
在Rt△ADE中,tanA==.
∵DE=3,∴AE=4,
∴AD==5,
∴AB=BD+AD=10+5=15.
在Rt△ABC中,tanA==,
设BC=3x,则AC=4x,∴AB=5x,
即5x=15,解得x=3.
∴AC=4x=12,
∴CE=AC-AE=12-4=8.
在Rt△CDE中,CD===.
16.解:如图,过点A作AD⊥BC于点D.
在Rt△ABD中,tanB==2.
在Rt△ACD中,tanC==.
设AD=x m,则BD=x m,CD=2x m.
∵BC=10 m,
∴x+2x=10,解得x=4.
故这块三角形草地的面积为AD·BC=×4×10=20(m2).
17.解:(1)由题意,得∠DBE=90°,∠ABC=60°,
∴∠A=∠CBE=30°.
又∵∠ACB=90°,BC=1,
∴AC=BC=,AB=2BC=2.
由旋转性质可知AC=A'C,BC=B'C,∠ACD=∠BCE,
从而△ADC∽△BEC,
∴=,即=,∴BE=x.
由上易得BD=2-x,
∴S=BE·BD=×x·(2-x)=-x2+x(0
∴-x2+x=××1×,
∴4x2-8x+3=0,∴x1=,x2=.
①当x=时,BD=2-=,BE=×=,
∴DE==.
∵DE∥A'B',∴∠EDC=∠A'=∠A=30°.
又∵∠A'CB'=90°,
∴EC=DE=>BE,
∴此时☉E与A'C相离.
过点D作DF⊥AC于点F,如图.
则DF=x=,AF=DF=,
∴CF=AC-AF=-= ,
∴tanα===.
②当x=时,BD=AB-AD=2-=,BE=×=,
∴DE==1,
同理可求EC=DE=
同理可求出tanα=.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
