苏科版数学九年级下册同步课时练习:7.6与坡度和坡角有关的问题(第1课时) (word版含答案)
文档属性
| 名称 | 苏科版数学九年级下册同步课时练习:7.6与坡度和坡角有关的问题(第1课时) (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 266.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-15 00:00:00 | ||
图片预览



文档简介
7.6 第1课时 与坡度和坡角有关的问题
知识点 坡度与坡角的概念
1.图一水库大坝横断面的一部分,坝高h=6 m,迎水坡AB=10 m,斜坡AB的坡角为α,则tanα的值为 ( )
A. B. C. D.
2.[2021·启东期末] 如图拦水坝的横断面,堤高BC为6米,斜面坡度为1∶2,则斜坡AB的长为 ( )
A.4米 B.6米 C.12米 D.24米
3.如图长4 m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为 ( )
A.2 m B.2 m C.(2-2)m D.(2-2)m
4.[2021·南京江宁区月考] 如图一斜坡的横截面,某人沿斜坡从点M出发,走了13米到达点N处,此时在铅垂方向上升了5米,那么该斜坡的坡度是 .
5.[2021·南通崇川区月考] 如图AB是一垂直于水平面的建筑物,BC是建筑物底端的一个平台,斜坡CD的坡度i为1∶0.75,坡长CD为10米,DE为地平面(点A,B,C,D,E均在同一平面内),则平台BC距地面DE的高度为 .
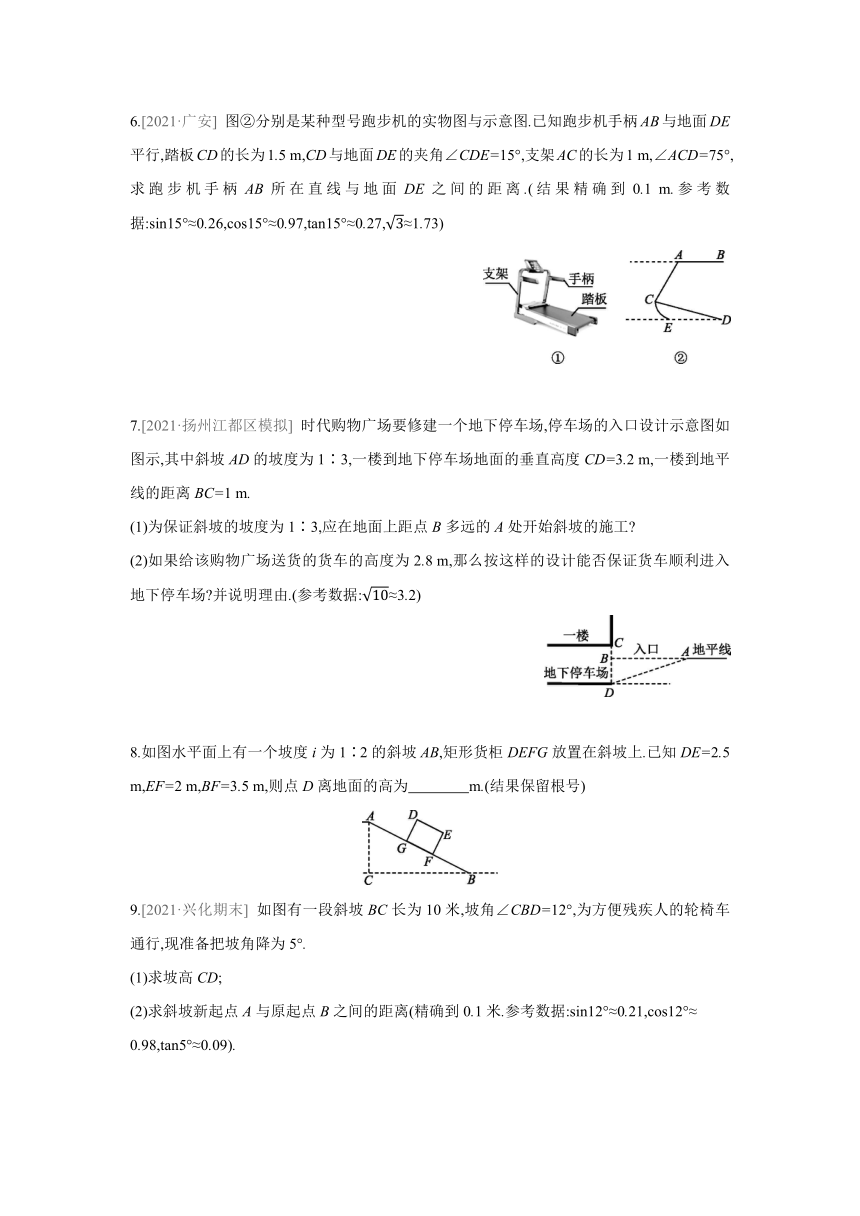
6.[2021·广安] 图②分别是某种型号跑步机的实物图与示意图.已知跑步机手柄AB与地面DE平行,踏板CD的长为1.5 m,CD与地面DE的夹角∠CDE=15°,支架AC的长为1 m,∠ACD=75°,求跑步机手柄AB所在直线与地面DE之间的距离.(结果精确到0.1 m.参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,≈1.73)
7.[2021·扬州江都区模拟] 时代购物广场要修建一个地下停车场,停车场的入口设计示意图如图示,其中斜坡AD的坡度为1∶3,一楼到地下停车场地面的垂直高度CD=3.2 m,一楼到地平线的距离BC=1 m.
(1)为保证斜坡的坡度为1∶3,应在地面上距点B多远的A处开始斜坡的施工
(2)如果给该购物广场送货的货车的高度为2.8 m,那么按这样的设计能否保证货车顺利进入地下停车场 并说明理由.(参考数据:≈3.2)
8.如图水平面上有一个坡度i为1∶2的斜坡AB,矩形货柜DEFG放置在斜坡上.已知DE=2.5 m,EF=2 m,BF=3.5 m,则点D离地面的高为 m.(结果保留根号)
9.[2021·兴化期末] 如图有一段斜坡BC长为10米,坡角∠CBD=12°,为方便残疾人的轮椅车通行,现准备把坡角降为5°.
(1)求坡高CD;
(2)求斜坡新起点A与原起点B之间的距离(精确到0.1米.参考数据:sin12°≈0.21,cos12°≈
0.98,tan5°≈0.09).
10.[2020·株洲] 某高速公路管理部门工作人员在对某段高速公路进行安全巡检过程中,发现该高速公路旁的一斜坡存在落石隐患.该斜坡横断面示意图如图②所示,水平线l1∥l2,点A,B分别在l1,l2上,斜坡AB的长为18米,过点B作BC⊥l1于点C,且线段AC的长为2米.
(1)求该斜坡的坡高BC(结果用最简根式表示);
(2)为降低落石风险,该管理部门计划对该斜坡进行改造,改造后的斜坡坡角α为60°,过点M作MN⊥l1于点N,求改造后的斜坡长度比改造前的斜坡长度增加了多少米.
11.如图,已知斜坡AB的长为60米,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示),修建一个平行于水平线CA的平台DE和一条新的斜坡BE.解答下面的问题:(下面两个小题的结果都精确到0.1米,参考数据:≈1.732)
(1)若修建的斜坡BE的坡角(即∠BEF)不大于45°,则平台DE的长最多为多少米
(2)一座建筑物GH距离坡脚点A 27米远(即AG=27米),小明在点D测得∠HDM为30°.点B,C,A,G,H在同一个平面上,点C,A,G在同一条直线上,且GH⊥CG,则建筑物GH的高为多少米
答案
7.6 第1课时 与坡度和坡角有关的问题
1.D
2.B ∵斜面坡度为1∶2,BC=6米,
∴AC=12米,则AB===6(米).
故选B.
3.B 在Rt△ABD中,
∵sin∠ABD=,
∴AD=AB·sin∠ABD=4sin60°=2(m).
在Rt△ACD中,∵sin∠ACD=,
∴AC===2(m).
故选B.
4.5∶12 如图,过点N作NG⊥AB于点G,再过点M作MH⊥NG于点H.
由题意,得MN=13,NH=5,
在Rt△MNH中,由勾股定理,得MH===12,
∴该斜坡的坡度为5∶12.
5.8米 如图,延长AB交ED的延长线于点F,过点C作CG⊥EF于点G,则BF=CG.在Rt△CDG中,i==1∶0.75=,CD=10米,∴设CG=4x米,则DG=3x米,由勾股定理得(4x)2+(3x)2=102,解得x=2(负值已舍去),∴CG=8米,∴BF=CG=8米,
即平台BC距地面DE的高度为8米.
6.解:如图,过点C作FG⊥AB交BA的延长线于点F,交DE的延长线于点G,
∴∠CFA=90°,∠CGD=90°.
∵CD与地面DE的夹角∠CDE=15°,∠ACD=75°,
∴∠ACF=∠FCD-∠ACD=∠CGD+∠CDE-∠ACD=90°+15°-75°=30°,
∴∠CAF=60°.
在Rt△ACF中,CF=AC·sin∠CAF=1×=(m).在Rt△CDG中,CG=CD·sin∠CDE=
1.5·sin15°≈1.5×0.26=0.39(m),∴FG=CF+CG≈+0.39≈1.3(m).故跑步机手柄AB所在直线与地面DE之间的距离约为1.3 m.
7.解:(1)∵CD=3.2 m,BC=1 m,
∴BD=2.2 m.
∵斜坡AD的坡度为1∶3,
∴=,即=,
解得AB=6.6(m).
答:应在地面上距点B 6.6 m的A处开始斜坡的施工.
(2)按这样的设计能保证货车顺利进入地下停车场.
理由:过点C作CH⊥AD于点H,如图.
则∠CDH+∠DCH=90°.
∵∠CDH+∠DAB=90°,
∴∠DCH=∠DAB,
∴tan∠DCH=tan∠DAB==.
设DH=x,则CH=3x.
在Rt△DCH中,由勾股定理,得CD==x,
由题意,得x=3.2,
解得x≈1,则CH≈3 m.
∵2.8<3,
∴按这样的设计能保证货车顺利进入地下停车场.
8.2 如图,过点D作DH⊥BC,垂足为H,且与AB相交于点S.
∵∠DGS=∠BHS,
∠DSG=∠BSH,
∴∠GDS=∠SBH,
∴tan∠GDS=tan∠SBH,即=.∵GD=EF=2 m,∴GS=1 m,∴DS==
m,BS=BF+FS=3.5+(2.5-1)=5(m).设HS=x m,则BH=2x m,∴x2+(2x)2=52,
解得x=(负值已舍去),则HS=m,∴DH=DS+HS=+=2(m).
9.解:(1)在Rt△CBD中,sin∠CBD=,
则CD=BC·sin∠CBD≈10×0.21=2.1.
答:坡高CD约为2.1米.
(2)在Rt△CBD中,cos∠CBD=,
则BD=BC·cos∠CBD≈10×0.98=9.8.
在Rt△CAD中,tan∠CAD=,
则AD=≈≈23.33,
则AB=AD-BD≈23.33-9.8≈13.5.
答:斜坡新起点A与原起点B之间的距离约为13.5米.
10.解:(1)在Rt△ABC中,BC===10(米).
答:该斜坡的坡高BC为10米.
(2)∵MN⊥l1,BC⊥l1,l1∥l2,
∴四边形BMNC为矩形,
∴MN=BC=10米.
在Rt△AMN中,sinα==,
∴AM==20米,
∴AM-AB=20-18=2(米).
答:改造后的斜坡长度比改造前的斜坡长度增加了2米.
11. (1)依题意,当∠BEF=45°时,可求得EF=BF,而BF=BD=AB=15米,所以DF=15米,所以DE=15-15≈10.98≈11.0(米);(2)要求建筑物GH的高,可过点D作DP⊥AC,垂足为P,进而利用锐角三角函数求解.
解:(1)当∠BEF=45°时,平台DE的长最大,此时EF=BF,而BF=BD=AB=15米,
所以DF=15米,
所以DE=DF-EF=15-15≈10.98≈11.0(米).
答:平台DE的长最多约为11.0米.
(2)过点D作DP⊥AC,垂足为P.
在Rt△DPA中,DP=AD=AB=×60=15(米),PA=AD·cos30°=×60×=15(米).
在矩形DPGM中,MG=DP=15米,DM=PG=PA+AG=(15+27)米.
在Rt△DMH中,HM=DM·tan30°=(15+27)×=(15+9)米,
所以GH=MG+HM=15+15+9≈45.6(米).
答:建筑物GH的高约为45.6米.
知识点 坡度与坡角的概念
1.图一水库大坝横断面的一部分,坝高h=6 m,迎水坡AB=10 m,斜坡AB的坡角为α,则tanα的值为 ( )
A. B. C. D.
2.[2021·启东期末] 如图拦水坝的横断面,堤高BC为6米,斜面坡度为1∶2,则斜坡AB的长为 ( )
A.4米 B.6米 C.12米 D.24米
3.如图长4 m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为 ( )
A.2 m B.2 m C.(2-2)m D.(2-2)m
4.[2021·南京江宁区月考] 如图一斜坡的横截面,某人沿斜坡从点M出发,走了13米到达点N处,此时在铅垂方向上升了5米,那么该斜坡的坡度是 .
5.[2021·南通崇川区月考] 如图AB是一垂直于水平面的建筑物,BC是建筑物底端的一个平台,斜坡CD的坡度i为1∶0.75,坡长CD为10米,DE为地平面(点A,B,C,D,E均在同一平面内),则平台BC距地面DE的高度为 .
6.[2021·广安] 图②分别是某种型号跑步机的实物图与示意图.已知跑步机手柄AB与地面DE平行,踏板CD的长为1.5 m,CD与地面DE的夹角∠CDE=15°,支架AC的长为1 m,∠ACD=75°,求跑步机手柄AB所在直线与地面DE之间的距离.(结果精确到0.1 m.参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,≈1.73)
7.[2021·扬州江都区模拟] 时代购物广场要修建一个地下停车场,停车场的入口设计示意图如图示,其中斜坡AD的坡度为1∶3,一楼到地下停车场地面的垂直高度CD=3.2 m,一楼到地平线的距离BC=1 m.
(1)为保证斜坡的坡度为1∶3,应在地面上距点B多远的A处开始斜坡的施工
(2)如果给该购物广场送货的货车的高度为2.8 m,那么按这样的设计能否保证货车顺利进入地下停车场 并说明理由.(参考数据:≈3.2)
8.如图水平面上有一个坡度i为1∶2的斜坡AB,矩形货柜DEFG放置在斜坡上.已知DE=2.5 m,EF=2 m,BF=3.5 m,则点D离地面的高为 m.(结果保留根号)
9.[2021·兴化期末] 如图有一段斜坡BC长为10米,坡角∠CBD=12°,为方便残疾人的轮椅车通行,现准备把坡角降为5°.
(1)求坡高CD;
(2)求斜坡新起点A与原起点B之间的距离(精确到0.1米.参考数据:sin12°≈0.21,cos12°≈
0.98,tan5°≈0.09).
10.[2020·株洲] 某高速公路管理部门工作人员在对某段高速公路进行安全巡检过程中,发现该高速公路旁的一斜坡存在落石隐患.该斜坡横断面示意图如图②所示,水平线l1∥l2,点A,B分别在l1,l2上,斜坡AB的长为18米,过点B作BC⊥l1于点C,且线段AC的长为2米.
(1)求该斜坡的坡高BC(结果用最简根式表示);
(2)为降低落石风险,该管理部门计划对该斜坡进行改造,改造后的斜坡坡角α为60°,过点M作MN⊥l1于点N,求改造后的斜坡长度比改造前的斜坡长度增加了多少米.
11.如图,已知斜坡AB的长为60米,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示),修建一个平行于水平线CA的平台DE和一条新的斜坡BE.解答下面的问题:(下面两个小题的结果都精确到0.1米,参考数据:≈1.732)
(1)若修建的斜坡BE的坡角(即∠BEF)不大于45°,则平台DE的长最多为多少米
(2)一座建筑物GH距离坡脚点A 27米远(即AG=27米),小明在点D测得∠HDM为30°.点B,C,A,G,H在同一个平面上,点C,A,G在同一条直线上,且GH⊥CG,则建筑物GH的高为多少米
答案
7.6 第1课时 与坡度和坡角有关的问题
1.D
2.B ∵斜面坡度为1∶2,BC=6米,
∴AC=12米,则AB===6(米).
故选B.
3.B 在Rt△ABD中,
∵sin∠ABD=,
∴AD=AB·sin∠ABD=4sin60°=2(m).
在Rt△ACD中,∵sin∠ACD=,
∴AC===2(m).
故选B.
4.5∶12 如图,过点N作NG⊥AB于点G,再过点M作MH⊥NG于点H.
由题意,得MN=13,NH=5,
在Rt△MNH中,由勾股定理,得MH===12,
∴该斜坡的坡度为5∶12.
5.8米 如图,延长AB交ED的延长线于点F,过点C作CG⊥EF于点G,则BF=CG.在Rt△CDG中,i==1∶0.75=,CD=10米,∴设CG=4x米,则DG=3x米,由勾股定理得(4x)2+(3x)2=102,解得x=2(负值已舍去),∴CG=8米,∴BF=CG=8米,
即平台BC距地面DE的高度为8米.
6.解:如图,过点C作FG⊥AB交BA的延长线于点F,交DE的延长线于点G,
∴∠CFA=90°,∠CGD=90°.
∵CD与地面DE的夹角∠CDE=15°,∠ACD=75°,
∴∠ACF=∠FCD-∠ACD=∠CGD+∠CDE-∠ACD=90°+15°-75°=30°,
∴∠CAF=60°.
在Rt△ACF中,CF=AC·sin∠CAF=1×=(m).在Rt△CDG中,CG=CD·sin∠CDE=
1.5·sin15°≈1.5×0.26=0.39(m),∴FG=CF+CG≈+0.39≈1.3(m).故跑步机手柄AB所在直线与地面DE之间的距离约为1.3 m.
7.解:(1)∵CD=3.2 m,BC=1 m,
∴BD=2.2 m.
∵斜坡AD的坡度为1∶3,
∴=,即=,
解得AB=6.6(m).
答:应在地面上距点B 6.6 m的A处开始斜坡的施工.
(2)按这样的设计能保证货车顺利进入地下停车场.
理由:过点C作CH⊥AD于点H,如图.
则∠CDH+∠DCH=90°.
∵∠CDH+∠DAB=90°,
∴∠DCH=∠DAB,
∴tan∠DCH=tan∠DAB==.
设DH=x,则CH=3x.
在Rt△DCH中,由勾股定理,得CD==x,
由题意,得x=3.2,
解得x≈1,则CH≈3 m.
∵2.8<3,
∴按这样的设计能保证货车顺利进入地下停车场.
8.2 如图,过点D作DH⊥BC,垂足为H,且与AB相交于点S.
∵∠DGS=∠BHS,
∠DSG=∠BSH,
∴∠GDS=∠SBH,
∴tan∠GDS=tan∠SBH,即=.∵GD=EF=2 m,∴GS=1 m,∴DS==
m,BS=BF+FS=3.5+(2.5-1)=5(m).设HS=x m,则BH=2x m,∴x2+(2x)2=52,
解得x=(负值已舍去),则HS=m,∴DH=DS+HS=+=2(m).
9.解:(1)在Rt△CBD中,sin∠CBD=,
则CD=BC·sin∠CBD≈10×0.21=2.1.
答:坡高CD约为2.1米.
(2)在Rt△CBD中,cos∠CBD=,
则BD=BC·cos∠CBD≈10×0.98=9.8.
在Rt△CAD中,tan∠CAD=,
则AD=≈≈23.33,
则AB=AD-BD≈23.33-9.8≈13.5.
答:斜坡新起点A与原起点B之间的距离约为13.5米.
10.解:(1)在Rt△ABC中,BC===10(米).
答:该斜坡的坡高BC为10米.
(2)∵MN⊥l1,BC⊥l1,l1∥l2,
∴四边形BMNC为矩形,
∴MN=BC=10米.
在Rt△AMN中,sinα==,
∴AM==20米,
∴AM-AB=20-18=2(米).
答:改造后的斜坡长度比改造前的斜坡长度增加了2米.
11. (1)依题意,当∠BEF=45°时,可求得EF=BF,而BF=BD=AB=15米,所以DF=15米,所以DE=15-15≈10.98≈11.0(米);(2)要求建筑物GH的高,可过点D作DP⊥AC,垂足为P,进而利用锐角三角函数求解.
解:(1)当∠BEF=45°时,平台DE的长最大,此时EF=BF,而BF=BD=AB=15米,
所以DF=15米,
所以DE=DF-EF=15-15≈10.98≈11.0(米).
答:平台DE的长最多约为11.0米.
(2)过点D作DP⊥AC,垂足为P.
在Rt△DPA中,DP=AD=AB=×60=15(米),PA=AD·cos30°=×60×=15(米).
在矩形DPGM中,MG=DP=15米,DM=PG=PA+AG=(15+27)米.
在Rt△DMH中,HM=DM·tan30°=(15+27)×=(15+9)米,
所以GH=MG+HM=15+15+9≈45.6(米).
答:建筑物GH的高约为45.6米.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
