苏科版数学九年级下册同步课时练习:第7章 锐角三角函数 自我综合评价 (word版含答案)
文档属性
| 名称 | 苏科版数学九年级下册同步课时练习:第7章 锐角三角函数 自我综合评价 (word版含答案) | 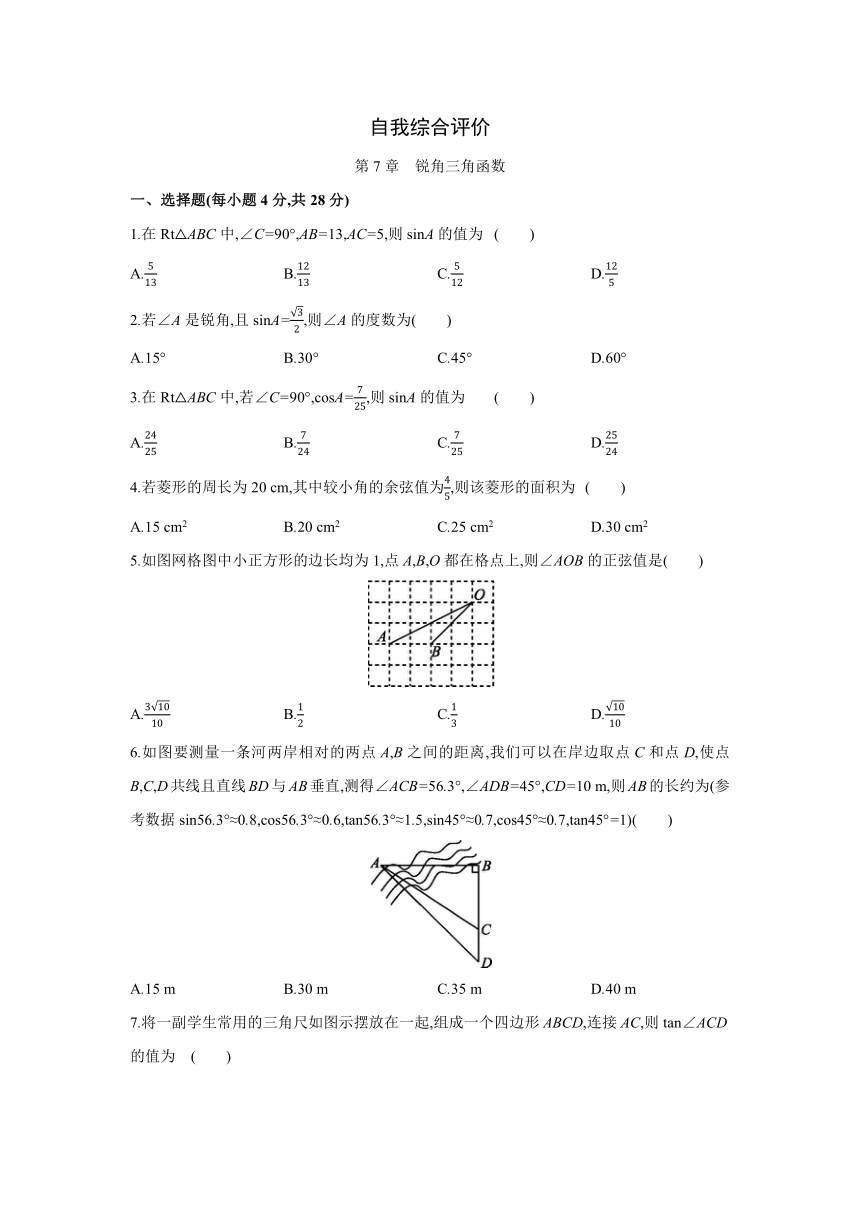 | |
| 格式 | docx | ||
| 文件大小 | 237.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-15 07:34:07 | ||
图片预览



文档简介
自我综合评价
第7章 锐角三角函数
一、选择题(每小题4分,共28分)
1.在Rt△ABC中,∠C=90°,AB=13,AC=5,则sinA的值为 ( )
A. B. C. D.
2.若∠A是锐角,且sinA=,则∠A的度数为( )
A.15° B.30° C.45° D.60°
3.在Rt△ABC中,若∠C=90°,cosA=,则sinA的值为 ( )
A. B. C. D.
4.若菱形的周长为20 cm,其中较小角的余弦值为,则该菱形的面积为 ( )
A.15 cm2 B.20 cm2 C.25 cm2 D.30 cm2
5.如图网格图中小正方形的边长均为1,点A,B,O都在格点上,则∠AOB的正弦值是( )
A. B. C. D.
6.如图要测量一条河两岸相对的两点A,B之间的距离,我们可以在岸边取点C和点D,使点B,C,D共线且直线BD与AB垂直,测得∠ACB=56.3°,∠ADB=45°,CD=10 m,则AB的长约为(参考数据sin56.3°≈0.8,cos56.3°≈0.6,tan56.3°≈1.5,sin45°≈0.7,cos45°≈0.7,tan45°=1)( )
A.15 m B.30 m C.35 m D.40 m
7.将一副学生常用的三角尺如图示摆放在一起,组成一个四边形ABCD,连接AC,则tan∠ACD的值为 ( )
A. B.+1 C.-1 D.2
二、填空题(每小题5分,共30分)
8.若锐角α满足9.已知锐角α,且sinα=cos35°,则α= 度.
10.在Rt△ABC中,∠C=90°,sinA=,BC=8,则AB= .
11.2022年在北京将举办第24届冬季奥运会,很多学校都开展了冰雪项目学习.如图滑雪轨道由AB,BC两部分组成,AB,BC的长度都为200米,一位同学乘滑雪板沿此轨道由点A滑到了点C,若AB与水平面的夹角α为30°,BC与水平面的夹角β为45°,则他下降的高度为
米(结果保留根号).
图 12.如图示,将矩形ABCD沿CE折叠,点B恰好落在边AD上的点F处,如果=,那么tan∠DCF的值是 .
13.如图在Rt△ABC中,∠ACB=90°,sinA=,点C关于直线AB的对称点为D,E为边AC上不与点A,C重合的动点,过点D作BE的垂线交BC于点F,则的值为 .
三、解答题(共42分)
14.(8分)计算:
tan230°+2sin60°+tan45°-tan60°+cos230°.
15.(10分)如图已知在△ABC中,AB=BC=5,tan∠ABC=.
(1)求边AC的长;
(2)设边BC的垂直平分线与边AB的交点为D,求的值.
16.(10分)如图在港口A处的正东方向有两个相距6 km的观测点B,C.一艘轮船从A处出发,沿北偏东26°方向航行至D处,在B,C处分别测得∠ABD=45°,∠C=37°.求轮船航行的距离AD.(参考数据:sin26°≈0.44,cos26°≈0.90,tan26°≈0.49,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
17.(14分)问题呈现
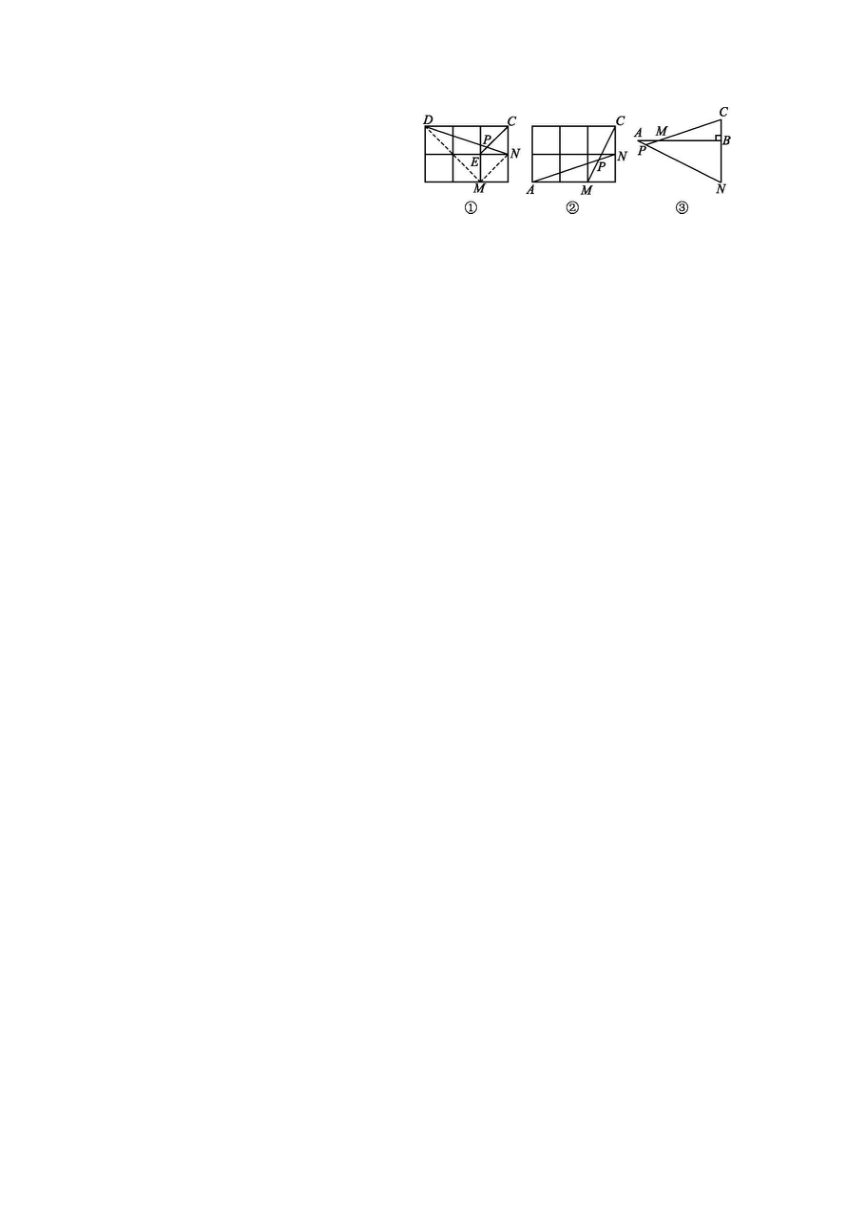
如图,在边长为1的正方形网格中,连接格点D,N和E,C,DN和EC相交于点P,求
tan∠CPN的值.
方法归纳
求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.通过观察我们发现问题中的∠CPN不在直角三角形中,则常常利用网格画平行线等方法解决此类问题,比如连接格点M,N,可得MN∥EC,则∠DNM=∠CPN,连接DM,那么∠CPN就变换到Rt△DMN中.
问题解决
(1)直接写出图①中tan∠CPN的值为 ;
(2)如图②,在边长为1的正方形网格中,AN与CM相交于点P,求cos∠CPN的值;
思维拓展
(3)如图③,AB⊥BC,AB=4BC,点M在AB上,且AM=BC,延长CB到点N,使BN=2BC,连接AN交CM的延长线于点P,用上述方法构造网格求∠CPN的度数.
答案
1.B 在Rt△ABC中,由勾股定理,得BC==12,∴sinA==.故选B.
2.D
3.A ∵在Rt△ABC中,∠C=90°,
∴∠A是锐角.
∵cosA==,
∴设AB=25x,则AC=7x,
由勾股定理得BC=24x,
∴sinA==.故选A.
4.A 如图,过点A作AE⊥BC于点E.
根据题意,得cosB=,
AB=BC=20×=5(cm).
在Rt△ABE中,BE=AB·cosB=5×=4(cm),
∴AE==3 cm,
∴该菱形的面积为5×3=15(cm2).
5.D 取格点C,连接AC,BC,观察图形可知,
点O,B,C共线,∠ACO=90°.
由勾股定理,得AC=,AO===2,
∴sin∠AOB===.故选D.
6.B 设AB=x m.
在Rt△ABD中,∵∠ADB=45°,∴AB=BD=x m.
在Rt△ABC中,∵∠ACB=56.3°,且tan∠ACB=,
∴BC==≈x.
由BC+CD=BD,得x+10=x,解得x=30,
∴AB的长约为30 m.故选B.
7.B 如图,过点A作AH⊥CB交CB的延长线于点H.
∵∠ABD=90°,∠DBC=45°,∴∠ABH=45°.
∵∠AHB=90°,
∴△ABH是等腰直角三角形,
∴AH=BH.设AH=BH=a,
则AB=a,BD=a,BC=CD=a,CH=a+a.
∵∠AHB=∠DCB=90°,∴AH∥DC,
∴∠ACD=∠CAH,
∴tan∠ACD=tan∠CAH==+1.
故选B.
8.45°<α<60° 9.55
10.10 在Rt△ABC中,∠C=90°,sinA=,BC=8,
∴sinA===,
∴AB=10.
11.(100+100) 过点A作AE⊥BM于点E,过点B作BF⊥CN于点F,如图.
∵α为30°,β为45°,AB=BC=200米,
∴sin30°=,sin45°=,
∴AE=AB·sin30°=100(米),
BF=BC·sin45°=100(米),
∴他下降的高度为AE+BF=(100+100)米.
12. 用特殊值法,设AB=2,BC=3,由折叠知CF=CB=3,由四边形ABCD是矩形知CD=AB=2.在Rt△CDF中,由勾股定理,得DF==,所以tan∠DCF==.
13. 如图,设DF交AB于点M,CD交AB于点N,BE交DF于点J.
∵∠ACB=90°,
∴sinA==,
∴可以假设BC=4k,则AB=5k,AC=3k.
∵点C,D关于AB对称,
∴CD⊥AB,CN=DN.
∵S△ABC=BC·AC=AB·CN,
∴CN=DN==k,
∴CD=k.
∵∠FCD+∠DCA=90°,∠DCA+∠A=90°,
∴∠DCF=∠A.
∵DF⊥BE,CD⊥AB,
∴∠BJM=∠DNM=90°.
∵∠BMJ=∠DMN,∴∠D=∠ABE,
∴△DCF∽△BAE,
∴===.
14.解:原式=2+2×+1-+2
=++1-+
=.
15.解:(1)过点A作AE⊥BC于点E.
在Rt△ABE中,tan∠ABC==,AB=5,
∴AE=3,BE=4,
∴CE=BC-BE=5-4=1.
在Rt△AEC中,根据勾股定理,得AC==.
(2)连接CD,设BC的垂直平分线与BC的交点为F.
∵DF垂直平分BC,
∴BD=CD,BF=CF=.
∵tan∠DBF==,
∴DF=.
在Rt△BFD中,根据勾股定理,得BD==,
∴AD=5-=,
∴=.
16.解:如图,过点D作DH⊥AC于点H.
在Rt△DCH中,∠C=37°,
∴CH=.
在Rt△DBH中,∠DBH=45°,
∴BH=.
∵BC=CH-BH,
∴-=6,
解得DH=18(km).
在Rt△DAH中,∠ADH=26°,
∴AD=≈20(km).
答:轮船航行的距离AD约为20 km.
17.解:(1)2
(2)如图①,取格点D,连接CD,DM.
∵CD∥AN,∴∠CPN=∠DCM.
∵DM=CM=,CD=,
∴DM2+CM2=CD2,
∴△DCM是等腰直角三角形,
∴∠DCM=45°,
∴cos∠CPN=cos∠DCM=.
(3)如图②,取格点Q,连接AQ,QN.
设小正方形的边长为1.
∵PC∥AQ,∴∠CPN=∠QAN.
∵AQ=QN=,AN=,
∴AQ2+QN2=AN2,
∴△AQN是等腰直角三角形,
∴∠QAN=45°,∴∠CPN=45°.
也可以这样做:如图③,取格点Q,连接AQ,QN.
设小正方形的边长为1.
∵PC∥QN,∴∠CPN=∠ANQ.
∵AQ=QN=,AN=,
∴AQ2+QN2=AN2,
∴△AQN是等腰直角三角形,
∴∠ANQ=45°,
∴∠CPN=45°.
第7章 锐角三角函数
一、选择题(每小题4分,共28分)
1.在Rt△ABC中,∠C=90°,AB=13,AC=5,则sinA的值为 ( )
A. B. C. D.
2.若∠A是锐角,且sinA=,则∠A的度数为( )
A.15° B.30° C.45° D.60°
3.在Rt△ABC中,若∠C=90°,cosA=,则sinA的值为 ( )
A. B. C. D.
4.若菱形的周长为20 cm,其中较小角的余弦值为,则该菱形的面积为 ( )
A.15 cm2 B.20 cm2 C.25 cm2 D.30 cm2
5.如图网格图中小正方形的边长均为1,点A,B,O都在格点上,则∠AOB的正弦值是( )
A. B. C. D.
6.如图要测量一条河两岸相对的两点A,B之间的距离,我们可以在岸边取点C和点D,使点B,C,D共线且直线BD与AB垂直,测得∠ACB=56.3°,∠ADB=45°,CD=10 m,则AB的长约为(参考数据sin56.3°≈0.8,cos56.3°≈0.6,tan56.3°≈1.5,sin45°≈0.7,cos45°≈0.7,tan45°=1)( )
A.15 m B.30 m C.35 m D.40 m
7.将一副学生常用的三角尺如图示摆放在一起,组成一个四边形ABCD,连接AC,则tan∠ACD的值为 ( )
A. B.+1 C.-1 D.2
二、填空题(每小题5分,共30分)
8.若锐角α满足
10.在Rt△ABC中,∠C=90°,sinA=,BC=8,则AB= .
11.2022年在北京将举办第24届冬季奥运会,很多学校都开展了冰雪项目学习.如图滑雪轨道由AB,BC两部分组成,AB,BC的长度都为200米,一位同学乘滑雪板沿此轨道由点A滑到了点C,若AB与水平面的夹角α为30°,BC与水平面的夹角β为45°,则他下降的高度为
米(结果保留根号).
图 12.如图示,将矩形ABCD沿CE折叠,点B恰好落在边AD上的点F处,如果=,那么tan∠DCF的值是 .
13.如图在Rt△ABC中,∠ACB=90°,sinA=,点C关于直线AB的对称点为D,E为边AC上不与点A,C重合的动点,过点D作BE的垂线交BC于点F,则的值为 .
三、解答题(共42分)
14.(8分)计算:
tan230°+2sin60°+tan45°-tan60°+cos230°.
15.(10分)如图已知在△ABC中,AB=BC=5,tan∠ABC=.
(1)求边AC的长;
(2)设边BC的垂直平分线与边AB的交点为D,求的值.
16.(10分)如图在港口A处的正东方向有两个相距6 km的观测点B,C.一艘轮船从A处出发,沿北偏东26°方向航行至D处,在B,C处分别测得∠ABD=45°,∠C=37°.求轮船航行的距离AD.(参考数据:sin26°≈0.44,cos26°≈0.90,tan26°≈0.49,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
17.(14分)问题呈现
如图,在边长为1的正方形网格中,连接格点D,N和E,C,DN和EC相交于点P,求
tan∠CPN的值.
方法归纳
求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.通过观察我们发现问题中的∠CPN不在直角三角形中,则常常利用网格画平行线等方法解决此类问题,比如连接格点M,N,可得MN∥EC,则∠DNM=∠CPN,连接DM,那么∠CPN就变换到Rt△DMN中.
问题解决
(1)直接写出图①中tan∠CPN的值为 ;
(2)如图②,在边长为1的正方形网格中,AN与CM相交于点P,求cos∠CPN的值;
思维拓展
(3)如图③,AB⊥BC,AB=4BC,点M在AB上,且AM=BC,延长CB到点N,使BN=2BC,连接AN交CM的延长线于点P,用上述方法构造网格求∠CPN的度数.
答案
1.B 在Rt△ABC中,由勾股定理,得BC==12,∴sinA==.故选B.
2.D
3.A ∵在Rt△ABC中,∠C=90°,
∴∠A是锐角.
∵cosA==,
∴设AB=25x,则AC=7x,
由勾股定理得BC=24x,
∴sinA==.故选A.
4.A 如图,过点A作AE⊥BC于点E.
根据题意,得cosB=,
AB=BC=20×=5(cm).
在Rt△ABE中,BE=AB·cosB=5×=4(cm),
∴AE==3 cm,
∴该菱形的面积为5×3=15(cm2).
5.D 取格点C,连接AC,BC,观察图形可知,
点O,B,C共线,∠ACO=90°.
由勾股定理,得AC=,AO===2,
∴sin∠AOB===.故选D.
6.B 设AB=x m.
在Rt△ABD中,∵∠ADB=45°,∴AB=BD=x m.
在Rt△ABC中,∵∠ACB=56.3°,且tan∠ACB=,
∴BC==≈x.
由BC+CD=BD,得x+10=x,解得x=30,
∴AB的长约为30 m.故选B.
7.B 如图,过点A作AH⊥CB交CB的延长线于点H.
∵∠ABD=90°,∠DBC=45°,∴∠ABH=45°.
∵∠AHB=90°,
∴△ABH是等腰直角三角形,
∴AH=BH.设AH=BH=a,
则AB=a,BD=a,BC=CD=a,CH=a+a.
∵∠AHB=∠DCB=90°,∴AH∥DC,
∴∠ACD=∠CAH,
∴tan∠ACD=tan∠CAH==+1.
故选B.
8.45°<α<60° 9.55
10.10 在Rt△ABC中,∠C=90°,sinA=,BC=8,
∴sinA===,
∴AB=10.
11.(100+100) 过点A作AE⊥BM于点E,过点B作BF⊥CN于点F,如图.
∵α为30°,β为45°,AB=BC=200米,
∴sin30°=,sin45°=,
∴AE=AB·sin30°=100(米),
BF=BC·sin45°=100(米),
∴他下降的高度为AE+BF=(100+100)米.
12. 用特殊值法,设AB=2,BC=3,由折叠知CF=CB=3,由四边形ABCD是矩形知CD=AB=2.在Rt△CDF中,由勾股定理,得DF==,所以tan∠DCF==.
13. 如图,设DF交AB于点M,CD交AB于点N,BE交DF于点J.
∵∠ACB=90°,
∴sinA==,
∴可以假设BC=4k,则AB=5k,AC=3k.
∵点C,D关于AB对称,
∴CD⊥AB,CN=DN.
∵S△ABC=BC·AC=AB·CN,
∴CN=DN==k,
∴CD=k.
∵∠FCD+∠DCA=90°,∠DCA+∠A=90°,
∴∠DCF=∠A.
∵DF⊥BE,CD⊥AB,
∴∠BJM=∠DNM=90°.
∵∠BMJ=∠DMN,∴∠D=∠ABE,
∴△DCF∽△BAE,
∴===.
14.解:原式=2+2×+1-+2
=++1-+
=.
15.解:(1)过点A作AE⊥BC于点E.
在Rt△ABE中,tan∠ABC==,AB=5,
∴AE=3,BE=4,
∴CE=BC-BE=5-4=1.
在Rt△AEC中,根据勾股定理,得AC==.
(2)连接CD,设BC的垂直平分线与BC的交点为F.
∵DF垂直平分BC,
∴BD=CD,BF=CF=.
∵tan∠DBF==,
∴DF=.
在Rt△BFD中,根据勾股定理,得BD==,
∴AD=5-=,
∴=.
16.解:如图,过点D作DH⊥AC于点H.
在Rt△DCH中,∠C=37°,
∴CH=.
在Rt△DBH中,∠DBH=45°,
∴BH=.
∵BC=CH-BH,
∴-=6,
解得DH=18(km).
在Rt△DAH中,∠ADH=26°,
∴AD=≈20(km).
答:轮船航行的距离AD约为20 km.
17.解:(1)2
(2)如图①,取格点D,连接CD,DM.
∵CD∥AN,∴∠CPN=∠DCM.
∵DM=CM=,CD=,
∴DM2+CM2=CD2,
∴△DCM是等腰直角三角形,
∴∠DCM=45°,
∴cos∠CPN=cos∠DCM=.
(3)如图②,取格点Q,连接AQ,QN.
设小正方形的边长为1.
∵PC∥AQ,∴∠CPN=∠QAN.
∵AQ=QN=,AN=,
∴AQ2+QN2=AN2,
∴△AQN是等腰直角三角形,
∴∠QAN=45°,∴∠CPN=45°.
也可以这样做:如图③,取格点Q,连接AQ,QN.
设小正方形的边长为1.
∵PC∥QN,∴∠CPN=∠ANQ.
∵AQ=QN=,AN=,
∴AQ2+QN2=AN2,
∴△AQN是等腰直角三角形,
∴∠ANQ=45°,
∴∠CPN=45°.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
