苏科版数学九年级下册期末综合复习专题训练 利用抛物线上点的特征解决问题 (word版含答案)
文档属性
| 名称 | 苏科版数学九年级下册期末综合复习专题训练 利用抛物线上点的特征解决问题 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 88.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-15 00:00:00 | ||
图片预览


文档简介
专题训练 利用抛物线上点的特征解决问题
运用一 求字母的值
1.[2020·徐州泉山区期末] 已知二次函数y=mx2+x+m(m-2)的图像经过原点,则m的值为( )
A.0或2 B.0 C.2 D.无法确定
2.[2020·泰州海陵区期末] 已知抛物线y=-x2+mx+4经过(-2,n)和(4,n)两点,则n的值为 .
3.[2020·如皋月考] 已知抛物线y=ax2+bx+c经过点(1,0),(3,0),且顶点为M,交y轴于点N,试用含a的代数式表示点M,N的坐标,若点M在直线y=3x+2上,求a的值.
运用二 求字母的取值范围
4.[2020·盐城亭湖区期末] 如图已知M(a,b)是函数y=-x2+x+2图像上的一个动点.若|a|<1,则b的取值范围是 .
5.[2020·扬州广陵区模拟] 如图抛物线y=ax2+bx+c过点(-1,0),(0,2),且顶点在第一象限,设M=4a+2b+c,则M的取值范围是 .
6.[2020·海门模拟] 如图已知二次函数y=x2+ax+3的图像经过点P(-2,3).
(1)求a的值和图像的顶点坐标.
(2)点Q(m,n)在该二次函数图像上.
①当m=2时,求n的值;
②若点Q到y轴的距离小于2,请根据图像直接写出n的取值范围.
运用三 求代数式的值或范围
7.[2020·宿迁一模改编] 若二次函数y=ax图像经过点(2,1),则2022-2a+b= .
8.[2020·连云港海州区期末] 已知抛物线y=-x2+bx+c经过(-1,a)和(3,a)两点,则a-c= .
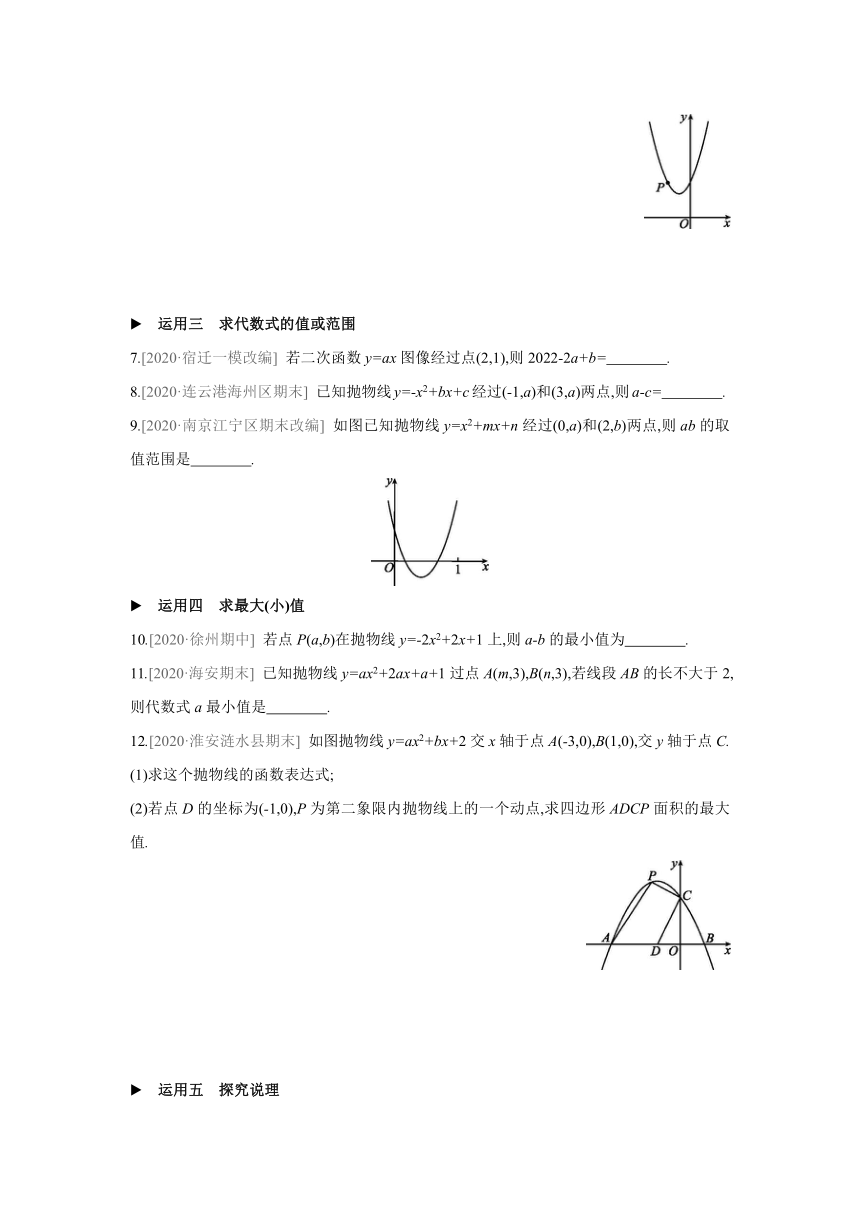
9.[2020·南京江宁区期末改编] 如图已知抛物线y=x2+mx+n经过(0,a)和(2,b)两点,则ab的取值范围是 .
运用四 求最大(小)值
10.[2020·徐州期中] 若点P(a,b)在抛物线y=-2x2+2x+1上,则a-b的最小值为 .
11.[2020·海安期末] 已知抛物线y=ax2+2ax+a+1过点A(m,3),B(n,3),若线段AB的长不大于2,则代数式a最小值是 .
12.[2020·淮安涟水县期末] 如图抛物线y=ax2+bx+2交x轴于点A(-3,0),B(1,0),交y轴于点C.
(1)求这个抛物线的函数表达式;
(2)若点D的坐标为(-1,0),P为第二象限内抛物线上的一个动点,求四边形ADCP面积的最大值.
运用五 探究说理
13.[2020·常州天宁区模拟] 已知抛物线y=2x2-4x+c与x轴有两个不同的交点.
(1)求c的取值范围;
(2)若抛物线y=2x2-4x+c经过点A(2,m)和点B(3,n),试比较m与n的大小,并说明理由.
14.[2020·兴化二模] 已知二次函数y=-2x2+bx+c(b,c为常数)的图像经过点(2,-1),其对称轴为直线x=1.
(1)求该二次函数的表达式.
(2)点P(0,n)在y轴上,若n<1,过点P作x轴的平行线与该二次函数的图像交于E,F两点,当n取某一范围内的任意实数时,|FP-EP|的值始终是一个定值d,求此时n的取值范围及定值d.
(3)是否存在两个不等实数s,t(s答案
1.C 根据题意,得m(m-2)=0,解得m1=0,m2=2.∵二次函数的二次项系数不为0,∴m=2.故选C.
2.-4 由抛物线y=-x2+mx+4经过(-2,n)和(4,n)两点,可知抛物线的对称轴为直线x=1,
∴=1,∴m=2,
∴y=-x2+2x+4.
将(-2,n)代入函数表达式,可得n=-4.
3.解:把点(1,0),(3,0)的坐标代入y=ax2+bx+c,
得解得
∴抛物线的表达式为y=ax2-4ax+3a,
∴对称轴为直线x=2.
把x=2代入,得y=4a-8a+3a=-a,
∴M(2,-a).
当x=0时,y=3a,∴N(0,3a).
当点M在直线y=3x+2上时,
把M(2,-a)代入y=3x+2,得3×2+2=-a,
∴a=-8.
4.0∵y=-x2+x+2=-x-2+,∴当x=时,y取得最大值,当x=-1时,y取得最小2-1+2=0.
结合图像可得b的取值范围是05.-60,a<0,
∴b>0,∴a>-2,∴-26.解:(1)把点P(-2,3)的坐标代入y=x2+ax+3,得(-2)2-2a+3=3,解得a=2,∴y=x2+2x+3=(x+1)2+2,
∴图像的顶点坐标为(-1,2).
(2)①当m=2时,n=11.
②∵点Q到y轴的距离小于2,
∴|m|<2,∴-27.2021 ∵二次函数y=ax图像经过点(2,1),∴41,∴2a-b=1,
∴2022-2a+b=2022-(2a-b)=2022-1=2021.故答案为2021.
8.-3 易知点(-1,a)和(3,a)关于抛物线的对称轴直线x=对称,∴3-=+1,解得b=2,即y=-x2+2x+c,把(-1,a)代入,得ac,∴
9.0令x=2,得b=(2-x1)(2-x2),
∴ab=x1x2(2-x1)(2-x2)=(2x1-)(2x2-)=[1-(x1-1)2][1-(x2-1)2].
∵0∴010.- ∵点P(a,b)在抛物线y=-2x2+2x+1上,∴b=-2a2+2a+1,
∴a-b=2+2a+1)=2a∵a-b=2a2a-2-,∴a-b的最小值为-.
11.0 ∵抛物线y=ax2+2ax+a+1=a(x+1)2+1,∴抛物线的顶点坐标为(-1,1).∵抛物线过点A(m,3),B(n,3),∴a>0.∵对称轴为直线x=-1,线段AB的长不大于2,∴a+1≥3,
∴a≥2,∴a最小值为20.
12.解:(1)把A(-3,0),B(1,0)代入y=ax2+bx+2,得
解得
∴抛物线的函数表达式为y=-x2-x+2.
(2)如图,连接OP.
当x=0时,y=2,∴C(0,2).
设点Px,-x2-x+2,
则S四边形ADCP=S△APO+S△CPO-S△ODC
=OA×yP+OC×|xP|-CO·OD
=×3×-x2-x+2+×2××2×1+2(-3∵-1<0,∴S四边形ADCP有最大值,∴当x=-时,S四边形ADCP取得最大值,为.
故四边形ADCP面积的最大值为.
13.解:(1)∵抛物线y=2x2-4x+c与x轴有两个不同的交点,
∴b2-4ac=16-8c>0,∴c<2.
(2)m∴点A(2,m)和点B(3,n)都在对称轴的右侧.
∵a=2>0,∴在对称轴右侧,y随x的增大而增大.
又∵2<3,∴m14.解:(1)由题意,得
解得∴y=-2x2+4x-1.
(2)n的取值范围为n≤-1,定值d=2.
(3)存在.令y'=11-6x.
∵-6<0,∴y'随x的增大而减小.
∴当s≤x≤t时,11-6t≤y'≤11-6s.
∵11-6t≤y≤11-6s,
∴若x=s,x=t在对称轴的同一侧,易知x=s,x=t时,y=y',即-2x2+4x-1=11-6x.
解得x1=2,x2=3.
∵抛物线y=-2x2+4x-1的对称轴为直线x=-=1,1<2<3,
∴s=2,t=3.
若x=s,x=t在对称轴的两侧,
∵y=-2x2+4x-1)2+1,
∴y≤1.
又∵11-6t≤y≤11-6s,
∴11-6s=1,∴s=.
∵s≤1,∴不成立.综上s=2,t=3.
运用一 求字母的值
1.[2020·徐州泉山区期末] 已知二次函数y=mx2+x+m(m-2)的图像经过原点,则m的值为( )
A.0或2 B.0 C.2 D.无法确定
2.[2020·泰州海陵区期末] 已知抛物线y=-x2+mx+4经过(-2,n)和(4,n)两点,则n的值为 .
3.[2020·如皋月考] 已知抛物线y=ax2+bx+c经过点(1,0),(3,0),且顶点为M,交y轴于点N,试用含a的代数式表示点M,N的坐标,若点M在直线y=3x+2上,求a的值.
运用二 求字母的取值范围
4.[2020·盐城亭湖区期末] 如图已知M(a,b)是函数y=-x2+x+2图像上的一个动点.若|a|<1,则b的取值范围是 .
5.[2020·扬州广陵区模拟] 如图抛物线y=ax2+bx+c过点(-1,0),(0,2),且顶点在第一象限,设M=4a+2b+c,则M的取值范围是 .
6.[2020·海门模拟] 如图已知二次函数y=x2+ax+3的图像经过点P(-2,3).
(1)求a的值和图像的顶点坐标.
(2)点Q(m,n)在该二次函数图像上.
①当m=2时,求n的值;
②若点Q到y轴的距离小于2,请根据图像直接写出n的取值范围.
运用三 求代数式的值或范围
7.[2020·宿迁一模改编] 若二次函数y=ax图像经过点(2,1),则2022-2a+b= .
8.[2020·连云港海州区期末] 已知抛物线y=-x2+bx+c经过(-1,a)和(3,a)两点,则a-c= .
9.[2020·南京江宁区期末改编] 如图已知抛物线y=x2+mx+n经过(0,a)和(2,b)两点,则ab的取值范围是 .
运用四 求最大(小)值
10.[2020·徐州期中] 若点P(a,b)在抛物线y=-2x2+2x+1上,则a-b的最小值为 .
11.[2020·海安期末] 已知抛物线y=ax2+2ax+a+1过点A(m,3),B(n,3),若线段AB的长不大于2,则代数式a最小值是 .
12.[2020·淮安涟水县期末] 如图抛物线y=ax2+bx+2交x轴于点A(-3,0),B(1,0),交y轴于点C.
(1)求这个抛物线的函数表达式;
(2)若点D的坐标为(-1,0),P为第二象限内抛物线上的一个动点,求四边形ADCP面积的最大值.
运用五 探究说理
13.[2020·常州天宁区模拟] 已知抛物线y=2x2-4x+c与x轴有两个不同的交点.
(1)求c的取值范围;
(2)若抛物线y=2x2-4x+c经过点A(2,m)和点B(3,n),试比较m与n的大小,并说明理由.
14.[2020·兴化二模] 已知二次函数y=-2x2+bx+c(b,c为常数)的图像经过点(2,-1),其对称轴为直线x=1.
(1)求该二次函数的表达式.
(2)点P(0,n)在y轴上,若n<1,过点P作x轴的平行线与该二次函数的图像交于E,F两点,当n取某一范围内的任意实数时,|FP-EP|的值始终是一个定值d,求此时n的取值范围及定值d.
(3)是否存在两个不等实数s,t(s
1.C 根据题意,得m(m-2)=0,解得m1=0,m2=2.∵二次函数的二次项系数不为0,∴m=2.故选C.
2.-4 由抛物线y=-x2+mx+4经过(-2,n)和(4,n)两点,可知抛物线的对称轴为直线x=1,
∴=1,∴m=2,
∴y=-x2+2x+4.
将(-2,n)代入函数表达式,可得n=-4.
3.解:把点(1,0),(3,0)的坐标代入y=ax2+bx+c,
得解得
∴抛物线的表达式为y=ax2-4ax+3a,
∴对称轴为直线x=2.
把x=2代入,得y=4a-8a+3a=-a,
∴M(2,-a).
当x=0时,y=3a,∴N(0,3a).
当点M在直线y=3x+2上时,
把M(2,-a)代入y=3x+2,得3×2+2=-a,
∴a=-8.
4.0
结合图像可得b的取值范围是0
∴b>0,∴a>-2,∴-2
∴图像的顶点坐标为(-1,2).
(2)①当m=2时,n=11.
②∵点Q到y轴的距离小于2,
∴|m|<2,∴-2
∴2022-2a+b=2022-(2a-b)=2022-1=2021.故答案为2021.
8.-3 易知点(-1,a)和(3,a)关于抛物线的对称轴直线x=对称,∴3-=+1,解得b=2,即y=-x2+2x+c,把(-1,a)代入,得ac,∴
9.0
∴ab=x1x2(2-x1)(2-x2)=(2x1-)(2x2-)=[1-(x1-1)2][1-(x2-1)2].
∵0
∴a-b=2+2a+1)=2a∵a-b=2a2a-2-,∴a-b的最小值为-.
11.0 ∵抛物线y=ax2+2ax+a+1=a(x+1)2+1,∴抛物线的顶点坐标为(-1,1).∵抛物线过点A(m,3),B(n,3),∴a>0.∵对称轴为直线x=-1,线段AB的长不大于2,∴a+1≥3,
∴a≥2,∴a最小值为20.
12.解:(1)把A(-3,0),B(1,0)代入y=ax2+bx+2,得
解得
∴抛物线的函数表达式为y=-x2-x+2.
(2)如图,连接OP.
当x=0时,y=2,∴C(0,2).
设点Px,-x2-x+2,
则S四边形ADCP=S△APO+S△CPO-S△ODC
=OA×yP+OC×|xP|-CO·OD
=×3×-x2-x+2+×2××2×1+2(-3
故四边形ADCP面积的最大值为.
13.解:(1)∵抛物线y=2x2-4x+c与x轴有两个不同的交点,
∴b2-4ac=16-8c>0,∴c<2.
(2)m
∵a=2>0,∴在对称轴右侧,y随x的增大而增大.
又∵2<3,∴m
解得∴y=-2x2+4x-1.
(2)n的取值范围为n≤-1,定值d=2.
(3)存在.令y'=11-6x.
∵-6<0,∴y'随x的增大而减小.
∴当s≤x≤t时,11-6t≤y'≤11-6s.
∵11-6t≤y≤11-6s,
∴若x=s,x=t在对称轴的同一侧,易知x=s,x=t时,y=y',即-2x2+4x-1=11-6x.
解得x1=2,x2=3.
∵抛物线y=-2x2+4x-1的对称轴为直线x=-=1,1<2<3,
∴s=2,t=3.
若x=s,x=t在对称轴的两侧,
∵y=-2x2+4x-1)2+1,
∴y≤1.
又∵11-6t≤y≤11-6s,
∴11-6s=1,∴s=.
∵s≤1,∴不成立.综上s=2,t=3.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
