苏科版数学九年级下册期末综合复习专题训练 相似形中的综合性问题 (word版含答案)
文档属性
| 名称 | 苏科版数学九年级下册期末综合复习专题训练 相似形中的综合性问题 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 181.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-15 07:43:42 | ||
图片预览



文档简介
专题训练 相似形中的综合性问题
类型一 三角形中的分类讨论
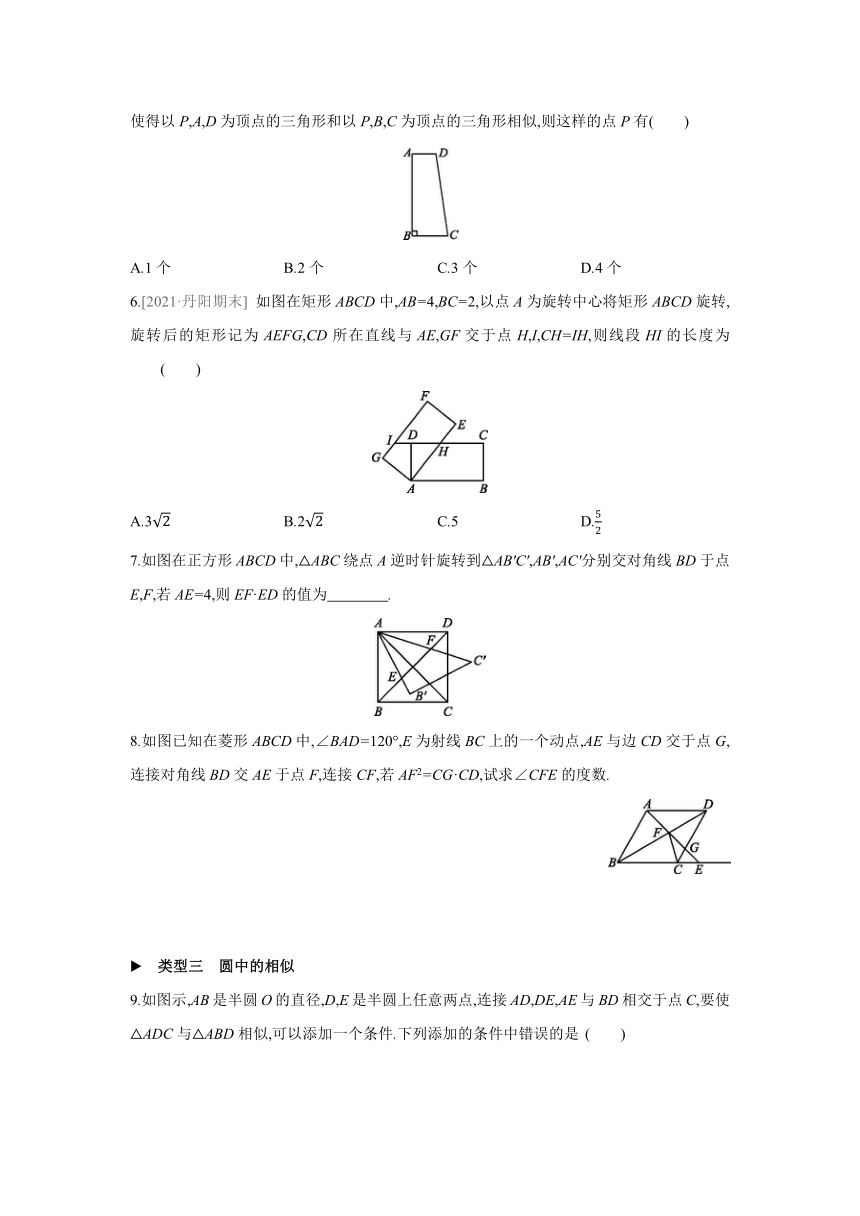
1.[2021·丹阳期末改编] 如图在Rt△ABC中,∠C=90°,AC=20,BC=15,点P在△ABC的斜边上,且AP=16,过点P画直线截△ABC,使截得的一个三角形与△ABC相似,则满足条件的截线共有 ( )
A.2条 B.3条 C.3条或4条 D.4条
2.将三角形纸片ABC按图示的方式折叠,使点B落在边AC上,记为点B',折痕为EF.已知AB=AC=8,BC=10.若以B',F,C为顶点的三角形与△ABC相似,则BF的长度是( )
A.5 B. C.或4 D.5或
3.如图在△ABC中,∠ACB=90°,AC=3,BC=2,以AC为斜边向外作Rt△ACD,当AD为何值时,这两个直角三角形相似
类型二 四边形中的相似
4.[2021·无锡新吴区期末] 如图在平行四边形ABCD中,E为BC的中点,DE,AC交于点F,则的值为 ( )
A. B. C. D.3
5.如图在直角梯形ABCD中,AD∥BC,∠B=90°,AB=7,AD=2,BC=3.若在线段AB上取一点P,使得以P,A,D为顶点的三角形和以P,B,C为顶点的三角形相似,则这样的点P有( )
A.1个 B.2个 C.3个 D.4个
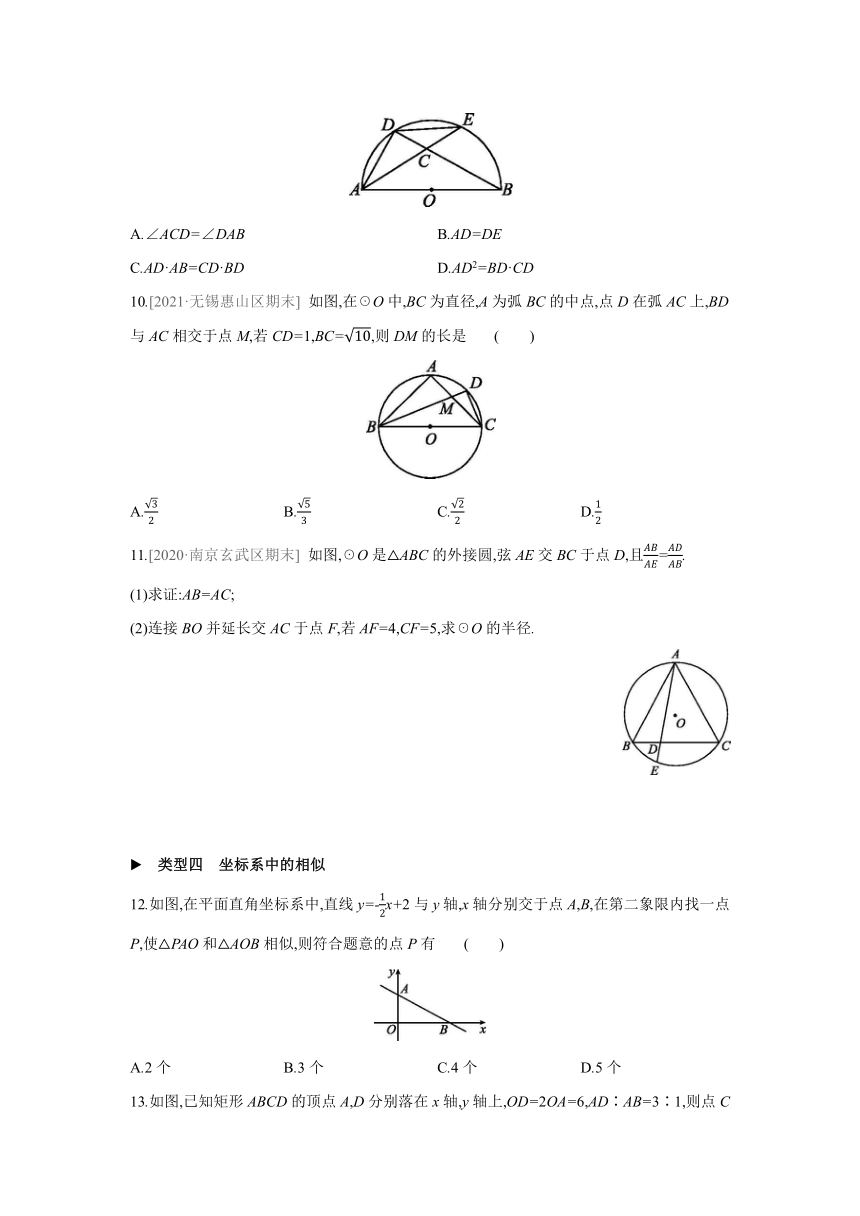
6.[2021·丹阳期末] 如图在矩形ABCD中,AB=4,BC=2,以点A为旋转中心将矩形ABCD旋转,旋转后的矩形记为AEFG,CD所在直线与AE,GF交于点H,I,CH=IH,则线段HI的长度为 ( )
A.3 B.2 C.5 D.
7.如图在正方形ABCD中,△ABC绕点A逆时针旋转到△AB'C',AB',AC'分别交对角线BD于点E,F,若AE=4,则EF·ED的值为 .
8.如图已知在菱形ABCD中,∠BAD=120°,E为射线BC上的一个动点,AE与边CD交于点G,连接对角线BD交AE于点F,连接CF,若AF2=CG·CD,试求∠CFE的度数.
类型三 圆中的相似
9.如图示,AB是半圆O的直径,D,E是半圆上任意两点,连接AD,DE,AE与BD相交于点C,要使△ADC与△ABD相似,可以添加一个条件.下列添加的条件中错误的是 ( )
A.∠ACD=∠DAB B.AD=DE
C.AD·AB=CD·BD D.AD2=BD·CD
10.[2021·无锡惠山区期末] 如图,在☉O中,BC为直径,A为弧BC的中点,点D在弧AC上,BD与AC相交于点M,若CD=1,BC=,则DM的长是 ( )
A. B. C. D.
11.[2020·南京玄武区期末] 如图,☉O是△ABC的外接圆,弦AE交BC于点D,且=.
(1)求证:AB=AC;
(2)连接BO并延长交AC于点F,若AF=4,CF=5,求☉O的半径.
类型四 坐标系中的相似
12.如图,在平面直角坐标系中,直线y=-x+2与y轴,x轴分别交于点A,B,在第二象限内找一点P,使△PAO和△AOB相似,则符合题意的点P有 ( )
A.2个 B.3个 C.4个 D.5个
13.如图,已知矩形ABCD的顶点A,D分别落在x轴,y轴上,OD=2OA=6,AD∶AB=3∶1,则点C的坐标是 ( )
A.(2,7) B.(3,7) C.(3,8) D.(4,8)
14.[2021·江阴期末] 如图,二次函数y=x2-x-2的图像与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,连接BC,在线段BC上有一动点P,过点P作y轴的平行线交二次函数的图像于点N,交x轴于点M,若△CPN与△BPM相似,则点P的坐标为 .
15.如图所示,在平面直角坐标系中,CB∥OA,OE=2EB,CB=3,OA=6,BA=3,OD=5.求证:△ODE∽△OBC.
答案
1.B
2.D 根据折叠的性质得到BF=B'F,根据相似三角形的性质得到B'F∶AB=FC∶BC或B'F∶AB=FC∶AC.设BF=x,则FC=10-x,即可求出x=或x=5.
3.解:在Rt△ABC中,由勾股定理可得AB==.
当△ABC∽△ACD时,=,
∴=,
∴AD=;
当△ABC∽△CAD时,=,
∴=,
∴AD=.
综上所述,当AD=或AD=时,这两个直角三角形相似.
4.A ∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴△ECF∽△DAF.
∵E为BC的中点,∴EC=BC=AD,
∴EF∶DF=EC∶AD=1∶2.
故选A.
5.C ①当△DAP∽△CBP时,AD∶BC=AP∶BP,将已知数据代入可得AP=;
②当△DAP∽△PBC时,AD∶BP=AP∶BC,将已知数据代入可得AP=1或AP=6.
所以这样的点P有3个.
故选C.
6.D 连接AI,AC.
∵以点A为旋转中心将矩形ABCD旋转,旋转后的矩形记为AEFG,
∴AG=AD,∠GAE=∠DAB=90°.
在Rt△AGI和Rt△ADI中,
∴Rt△AGI≌Rt△ADI(HL),
∴∠GAI=∠DAI,
∴90°-∠GAI=90°-∠DAI,
∴∠IAH=∠AID,∴IH=AH.
又∵IH=HC,∴IH=HC=AH,
∴∠IAC=90°,
∴∠DAI+∠DAC=90°.
又∵∠DAC+∠DCA=90°,
∴∠DAI=∠DCA.
又∵∠ADI=∠ADC=90°,
∴△ADI∽△CDA,
∴=,∴=,
∴DI=1,∴CI=ID+CD=5,
∴IH=CI=.故选D.
7.16 ∵四边形ABCD是正方形,
∴∠BAC=∠ADB=45°.
∵把△ABC绕点A逆时针旋转到△AB'C',
∴∠EAF=45°=∠ADB.
∵∠AEF=∠DEA,∴△AEF∽△DEA,
∴=,
∴EF·ED=AE2.
∵AE=4,∴EF·ED的值为16.
8.解:∵AF2=CG·CD,∴=.
∵四边形ABCD是菱形,
∴AB=BC,∠ABD=∠CBD,AB∥CD.
∵BF=BF,∴△ABF≌△CBF(SAS),
∴AF=CF,∴=,∴=.
又∵∠FCG=∠DCF,∴△FCG∽△DCF,
∴∠CFE=∠FDC.
∵AB∥CD,∴∠BAD+∠ADC=180°.
∵∠BAD=120°,∴∠ADC=60°.
∵四边形ABCD是菱形,
∴∠FDC=∠ADC=30°,
∴∠CFE=30°.
9.C
10.D ∵BC为☉O的直径,A为弧BC的中点,
∴∠BAC=∠BDC=90°,=,
∴AB=AC.
在Rt△BDC中,BD===3.
在Rt△BAC中,AB2+AC2=BC2,
∴AB=.
∵∠A=∠D,∠AMB=∠DMC,
∴△ABM∽△DCM,∴=,
∴=,∴AM=DM.
∵AB2+AM2=BM2,
∴5+5DM2=(3-DM)2,
解得DM=或DM=-2(不合题意,舍去).
故选D.
11.解:(1)证明:连接BE.
∵=,∠BAD=∠EAB,
∴△ABD∽△AEB,∴∠ABD=∠AEB.
又∠C=∠AEB,∴∠ABD=∠C,
∴AB=AC.
(2)如图,连接BO并延长交AC于点F,连接OC,连接AO并延长交BC于点H.
设☉O的半径为r.
∵AF=4,CF=5,
∴AB=AC=AF+CF=4+5=9.
∵AB=AC,OB=OC,
∴点A,O在BC的垂直平分线上,
∴AH⊥BC.
又AB=AC,∴AH平分∠BAC,
∴∠BAH=∠CAH.
∵OA=OB,∴∠BAH=∠ABF.
∴∠CAH=∠ABF.
又∵∠AFB=∠OFA,
∴△AFB∽△OFA,
∴==,
即==,
∴OF=r.
∴=,
∴r=.
12.C
13.A 如图,过点C作CE⊥y轴,垂足为E.
∵OD=2OA=6,
∴OA=3.
∵∠CED=∠CDA=90°,
∴∠ECD+∠CDE=90°,∠CDE+∠ODA=90°,
∴∠ECD=∠ODA.
又∵∠CED=∠DOA=90°,
∴△CED∽△DOA,∴==.
∵四边形ABCD是矩形,∴CD=AB,
∴==,
∴CE=2,DE=1,∴OE=7,
∴点C的坐标为(2,7).
14.,-或,- 对于抛物线y=x2-x-2,令x=0,得到y=-2,可得C(0,-2);
令y=0,可得0=x2-x-2,解得x=3或x=-,∴A-,0,B(3,0),
∴直线BC的函数表达式为y=x-2.
设Pm,m-2.
∵∠BPM=∠CPN,当CN∥AB时,∠PBM=∠PCN,此时△PCN∽△PBM,
∴把y=-2代入y=x2-x-2得x=或x=0(舍去),
∴N,-2,∴P,-;
当NC⊥BC时,∠PCN=∠PMB=90°,此时△PCN∽△PMB,过点N作NH⊥y轴于点H,
∴∠BOC=∠CHN=90°,∠OCB+∠NCH=90°.
又∵∠OCB+∠OBC=90°,
∴∠OBC=∠NCH,∴△OBC∽△HCN,
∴=,∴==.
又∵Nm,m2-m-2.
∴=,
∴m=(m=0已舍去),
∴P,-.
综上所述,满足条件的点P的坐标为,-或,-.
15.证明:过点B作BG⊥x轴于点G.
∵CB∥OA,∠COA=90°,
∴∠OCB=90°.
又∵BG⊥x 轴,
∴四边形BCOG为矩形,
∴BG=OC,BC=OG.
∵CB=3,∴OG=3,
∴GA=OA-OG=6-3=3.
在Rt△AGB中,BG2=AB2-GA2=(3)2-32=36,
∴BG=6,∴OC=6.
在Rt△OBG中,OB==3.
由OE=2BE,得OE=2,BE=,
∴==.
又∵∠DOE=∠BOC,
∴△ODE∽△OBC.
类型一 三角形中的分类讨论
1.[2021·丹阳期末改编] 如图在Rt△ABC中,∠C=90°,AC=20,BC=15,点P在△ABC的斜边上,且AP=16,过点P画直线截△ABC,使截得的一个三角形与△ABC相似,则满足条件的截线共有 ( )
A.2条 B.3条 C.3条或4条 D.4条
2.将三角形纸片ABC按图示的方式折叠,使点B落在边AC上,记为点B',折痕为EF.已知AB=AC=8,BC=10.若以B',F,C为顶点的三角形与△ABC相似,则BF的长度是( )
A.5 B. C.或4 D.5或
3.如图在△ABC中,∠ACB=90°,AC=3,BC=2,以AC为斜边向外作Rt△ACD,当AD为何值时,这两个直角三角形相似
类型二 四边形中的相似
4.[2021·无锡新吴区期末] 如图在平行四边形ABCD中,E为BC的中点,DE,AC交于点F,则的值为 ( )
A. B. C. D.3
5.如图在直角梯形ABCD中,AD∥BC,∠B=90°,AB=7,AD=2,BC=3.若在线段AB上取一点P,使得以P,A,D为顶点的三角形和以P,B,C为顶点的三角形相似,则这样的点P有( )
A.1个 B.2个 C.3个 D.4个
6.[2021·丹阳期末] 如图在矩形ABCD中,AB=4,BC=2,以点A为旋转中心将矩形ABCD旋转,旋转后的矩形记为AEFG,CD所在直线与AE,GF交于点H,I,CH=IH,则线段HI的长度为 ( )
A.3 B.2 C.5 D.
7.如图在正方形ABCD中,△ABC绕点A逆时针旋转到△AB'C',AB',AC'分别交对角线BD于点E,F,若AE=4,则EF·ED的值为 .
8.如图已知在菱形ABCD中,∠BAD=120°,E为射线BC上的一个动点,AE与边CD交于点G,连接对角线BD交AE于点F,连接CF,若AF2=CG·CD,试求∠CFE的度数.
类型三 圆中的相似
9.如图示,AB是半圆O的直径,D,E是半圆上任意两点,连接AD,DE,AE与BD相交于点C,要使△ADC与△ABD相似,可以添加一个条件.下列添加的条件中错误的是 ( )
A.∠ACD=∠DAB B.AD=DE
C.AD·AB=CD·BD D.AD2=BD·CD
10.[2021·无锡惠山区期末] 如图,在☉O中,BC为直径,A为弧BC的中点,点D在弧AC上,BD与AC相交于点M,若CD=1,BC=,则DM的长是 ( )
A. B. C. D.
11.[2020·南京玄武区期末] 如图,☉O是△ABC的外接圆,弦AE交BC于点D,且=.
(1)求证:AB=AC;
(2)连接BO并延长交AC于点F,若AF=4,CF=5,求☉O的半径.
类型四 坐标系中的相似
12.如图,在平面直角坐标系中,直线y=-x+2与y轴,x轴分别交于点A,B,在第二象限内找一点P,使△PAO和△AOB相似,则符合题意的点P有 ( )
A.2个 B.3个 C.4个 D.5个
13.如图,已知矩形ABCD的顶点A,D分别落在x轴,y轴上,OD=2OA=6,AD∶AB=3∶1,则点C的坐标是 ( )
A.(2,7) B.(3,7) C.(3,8) D.(4,8)
14.[2021·江阴期末] 如图,二次函数y=x2-x-2的图像与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,连接BC,在线段BC上有一动点P,过点P作y轴的平行线交二次函数的图像于点N,交x轴于点M,若△CPN与△BPM相似,则点P的坐标为 .
15.如图所示,在平面直角坐标系中,CB∥OA,OE=2EB,CB=3,OA=6,BA=3,OD=5.求证:△ODE∽△OBC.
答案
1.B
2.D 根据折叠的性质得到BF=B'F,根据相似三角形的性质得到B'F∶AB=FC∶BC或B'F∶AB=FC∶AC.设BF=x,则FC=10-x,即可求出x=或x=5.
3.解:在Rt△ABC中,由勾股定理可得AB==.
当△ABC∽△ACD时,=,
∴=,
∴AD=;
当△ABC∽△CAD时,=,
∴=,
∴AD=.
综上所述,当AD=或AD=时,这两个直角三角形相似.
4.A ∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴△ECF∽△DAF.
∵E为BC的中点,∴EC=BC=AD,
∴EF∶DF=EC∶AD=1∶2.
故选A.
5.C ①当△DAP∽△CBP时,AD∶BC=AP∶BP,将已知数据代入可得AP=;
②当△DAP∽△PBC时,AD∶BP=AP∶BC,将已知数据代入可得AP=1或AP=6.
所以这样的点P有3个.
故选C.
6.D 连接AI,AC.
∵以点A为旋转中心将矩形ABCD旋转,旋转后的矩形记为AEFG,
∴AG=AD,∠GAE=∠DAB=90°.
在Rt△AGI和Rt△ADI中,
∴Rt△AGI≌Rt△ADI(HL),
∴∠GAI=∠DAI,
∴90°-∠GAI=90°-∠DAI,
∴∠IAH=∠AID,∴IH=AH.
又∵IH=HC,∴IH=HC=AH,
∴∠IAC=90°,
∴∠DAI+∠DAC=90°.
又∵∠DAC+∠DCA=90°,
∴∠DAI=∠DCA.
又∵∠ADI=∠ADC=90°,
∴△ADI∽△CDA,
∴=,∴=,
∴DI=1,∴CI=ID+CD=5,
∴IH=CI=.故选D.
7.16 ∵四边形ABCD是正方形,
∴∠BAC=∠ADB=45°.
∵把△ABC绕点A逆时针旋转到△AB'C',
∴∠EAF=45°=∠ADB.
∵∠AEF=∠DEA,∴△AEF∽△DEA,
∴=,
∴EF·ED=AE2.
∵AE=4,∴EF·ED的值为16.
8.解:∵AF2=CG·CD,∴=.
∵四边形ABCD是菱形,
∴AB=BC,∠ABD=∠CBD,AB∥CD.
∵BF=BF,∴△ABF≌△CBF(SAS),
∴AF=CF,∴=,∴=.
又∵∠FCG=∠DCF,∴△FCG∽△DCF,
∴∠CFE=∠FDC.
∵AB∥CD,∴∠BAD+∠ADC=180°.
∵∠BAD=120°,∴∠ADC=60°.
∵四边形ABCD是菱形,
∴∠FDC=∠ADC=30°,
∴∠CFE=30°.
9.C
10.D ∵BC为☉O的直径,A为弧BC的中点,
∴∠BAC=∠BDC=90°,=,
∴AB=AC.
在Rt△BDC中,BD===3.
在Rt△BAC中,AB2+AC2=BC2,
∴AB=.
∵∠A=∠D,∠AMB=∠DMC,
∴△ABM∽△DCM,∴=,
∴=,∴AM=DM.
∵AB2+AM2=BM2,
∴5+5DM2=(3-DM)2,
解得DM=或DM=-2(不合题意,舍去).
故选D.
11.解:(1)证明:连接BE.
∵=,∠BAD=∠EAB,
∴△ABD∽△AEB,∴∠ABD=∠AEB.
又∠C=∠AEB,∴∠ABD=∠C,
∴AB=AC.
(2)如图,连接BO并延长交AC于点F,连接OC,连接AO并延长交BC于点H.
设☉O的半径为r.
∵AF=4,CF=5,
∴AB=AC=AF+CF=4+5=9.
∵AB=AC,OB=OC,
∴点A,O在BC的垂直平分线上,
∴AH⊥BC.
又AB=AC,∴AH平分∠BAC,
∴∠BAH=∠CAH.
∵OA=OB,∴∠BAH=∠ABF.
∴∠CAH=∠ABF.
又∵∠AFB=∠OFA,
∴△AFB∽△OFA,
∴==,
即==,
∴OF=r.
∴=,
∴r=.
12.C
13.A 如图,过点C作CE⊥y轴,垂足为E.
∵OD=2OA=6,
∴OA=3.
∵∠CED=∠CDA=90°,
∴∠ECD+∠CDE=90°,∠CDE+∠ODA=90°,
∴∠ECD=∠ODA.
又∵∠CED=∠DOA=90°,
∴△CED∽△DOA,∴==.
∵四边形ABCD是矩形,∴CD=AB,
∴==,
∴CE=2,DE=1,∴OE=7,
∴点C的坐标为(2,7).
14.,-或,- 对于抛物线y=x2-x-2,令x=0,得到y=-2,可得C(0,-2);
令y=0,可得0=x2-x-2,解得x=3或x=-,∴A-,0,B(3,0),
∴直线BC的函数表达式为y=x-2.
设Pm,m-2.
∵∠BPM=∠CPN,当CN∥AB时,∠PBM=∠PCN,此时△PCN∽△PBM,
∴把y=-2代入y=x2-x-2得x=或x=0(舍去),
∴N,-2,∴P,-;
当NC⊥BC时,∠PCN=∠PMB=90°,此时△PCN∽△PMB,过点N作NH⊥y轴于点H,
∴∠BOC=∠CHN=90°,∠OCB+∠NCH=90°.
又∵∠OCB+∠OBC=90°,
∴∠OBC=∠NCH,∴△OBC∽△HCN,
∴=,∴==.
又∵Nm,m2-m-2.
∴=,
∴m=(m=0已舍去),
∴P,-.
综上所述,满足条件的点P的坐标为,-或,-.
15.证明:过点B作BG⊥x轴于点G.
∵CB∥OA,∠COA=90°,
∴∠OCB=90°.
又∵BG⊥x 轴,
∴四边形BCOG为矩形,
∴BG=OC,BC=OG.
∵CB=3,∴OG=3,
∴GA=OA-OG=6-3=3.
在Rt△AGB中,BG2=AB2-GA2=(3)2-32=36,
∴BG=6,∴OC=6.
在Rt△OBG中,OB==3.
由OE=2BE,得OE=2,BE=,
∴==.
又∵∠DOE=∠BOC,
∴△ODE∽△OBC.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
