2.2.2反证法

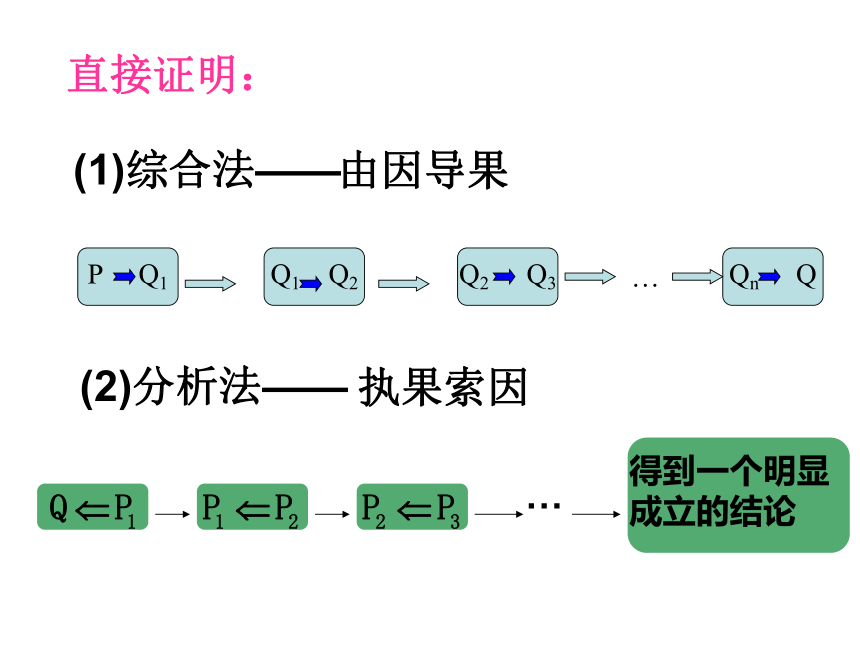
课件26张PPT。2.2.2 反证法直接证明：(1)综合法——(2)分析法——由因导果执果索因 将9个球分别染成红色或白色。那么无论怎样染，至少有5个球是同色的。你能证明这个结论吗？引例1：间接证明： 不是直接从原命题的条件逐步推得命题成立的证明方法。反证法是一种常用的间接证明的方法。 反证法：
假设命题结论的反面成立，经过正确的推理,引出矛盾，因此说明假设错误,从而证明原命题成立,这样的的证明方法叫反证法。反证法的思维方法：
正难则反 一般地，假设原命题不成立， 经过正确的推理，最后得出矛盾。 因此说明假设错误，从而证明了原命题成立， 这样的证明方法叫做反证法（归谬法）。其过程包括：反设——假设命题的结论不成立；存真——由矛盾结果，断定反设不真，从而肯定原结论成立。归谬——从假设出发，经过一系列正确的推理，得出矛盾；归缪矛盾：
（1）与已知条件矛盾；
（2）与已有公理、定理、定义矛盾；
（3）自相矛盾。例1 已知a≠0，证明x的方程ax=b
有且只有一个根。 应用反证法的情形：
(1)直接证明困难;
(2)需分成很多类进行讨论．
（3)结论为“至少”、“至多”、“有无穷多个” ---类命题；
（4）结论为 “唯一”类命题；正难则反!常见否定用语是－－－不是 有－－－没有
等－－－不等 成立－－不成立
都是－－不都是，即至少有一个不是
都有－－不都有，即至少有一个没有
都不是－部分或全部是，即至少有一个是
唯一－－至少有两个
至少有一个有（是）－－全部没有（不是）
至少有一个不－－－－－全部都例3：证明：圆的两条不全是直径的相交弦不能互相平分.已知：在⊙O中,弦AB、CD相交于P，且AB、CD不全是直径 求证：AB、CD不能互相平分。ABCD用反证法证明：圆的两条不是直径的相交弦不能互相平分。已知：如图，在⊙O中，弦AB、CD交于点P，且AB、CD不是直径.求证：弦AB、CD不被P平分.例 1证明：假设弦AB、CD被P平分，连结 AD、BD、BC、AC, 因为弦AB、CD被P点平分，所以四边形ACBD是平行四边形所以因为 ABCD为圆内接四边形所以因此所以，对角线AB、CD均为直径，这与已知条件矛盾，即假设不成立所以，弦AB、CD不被P平分。用反证法证明：圆的两条不是直径的相交弦不能互相平分。已知：如图，在⊙O中，弦AB、CD交于点P，且AB、CD不是直径.求证：弦AB、CD不被P平分.例 1由于P点一定不是圆心O，连结OP，根据垂径定理的推论，有所以，弦AB、CD不被P平分。证明：假设弦AB、CD被P平分，即过点P有两条直线与OP都垂直，这与垂线性质矛盾，即假设不成立证法二OP⊥AB，OP⊥CD，演练反馈2、平面内有四个点，没有三点共线，
证明：以任意三个点为顶点的三角形不可能都是锐角三角形这与一个周角为360°矛盾。 演练反馈2、平面内有四个点，没有三点共线，
证明：以任意三个点为顶点的三角形不可能都是锐角三角形都是锐角三角形，即这与四边形内角和矛盾。所以，综上所述，假设不成立，从而题目结论成立。即这些三角形不可能都为锐角三角形。总结提炼1.用反证法证明命题的一般步骤是什么? 用反证法在归谬中所导出的矛盾可以是与题设矛盾,与假设矛盾,与已知定义、公理、定理矛盾，自相矛盾等．①反设 ②归谬 ③结论2.用反证法证题,矛盾的主要类型有哪些?推理 合情推理 演绎推理
（归纳、类比） （三段论）证明 直接证明 间接证明
（分析法、综合法） （反证法）数学—公理化思想例1：用反证法证明：
如果a>b>0，那么 例4 求证： 是无理数。作业思考？ A、B、C三个人，A说B撒谎，B说C撒谎，C说A、B都撒谎。则C必定是在撒谎，为什么？分析:假设C没有撒谎, 则C真. - - -- -那么A假且B假;由A假, 知B真. 这与B假矛盾.那么假设C没有撒谎不成立;则C必定是在撒谎.思考题:甲、乙、丙三箱共有小球384个,先由甲箱取出若干放进乙、丙两箱内,所放个数分别为乙、丙箱内原有个数,继而由乙箱取出若干个球放进甲、丙两箱内,最后由丙箱取出若干个球放进甲、乙两箱内,方法同前.结果三箱内的小球数恰好相等.求甲、乙、丙三箱原有小球数甲:208个,乙:112个,丙:64个