数系的扩充和复数的概念学案

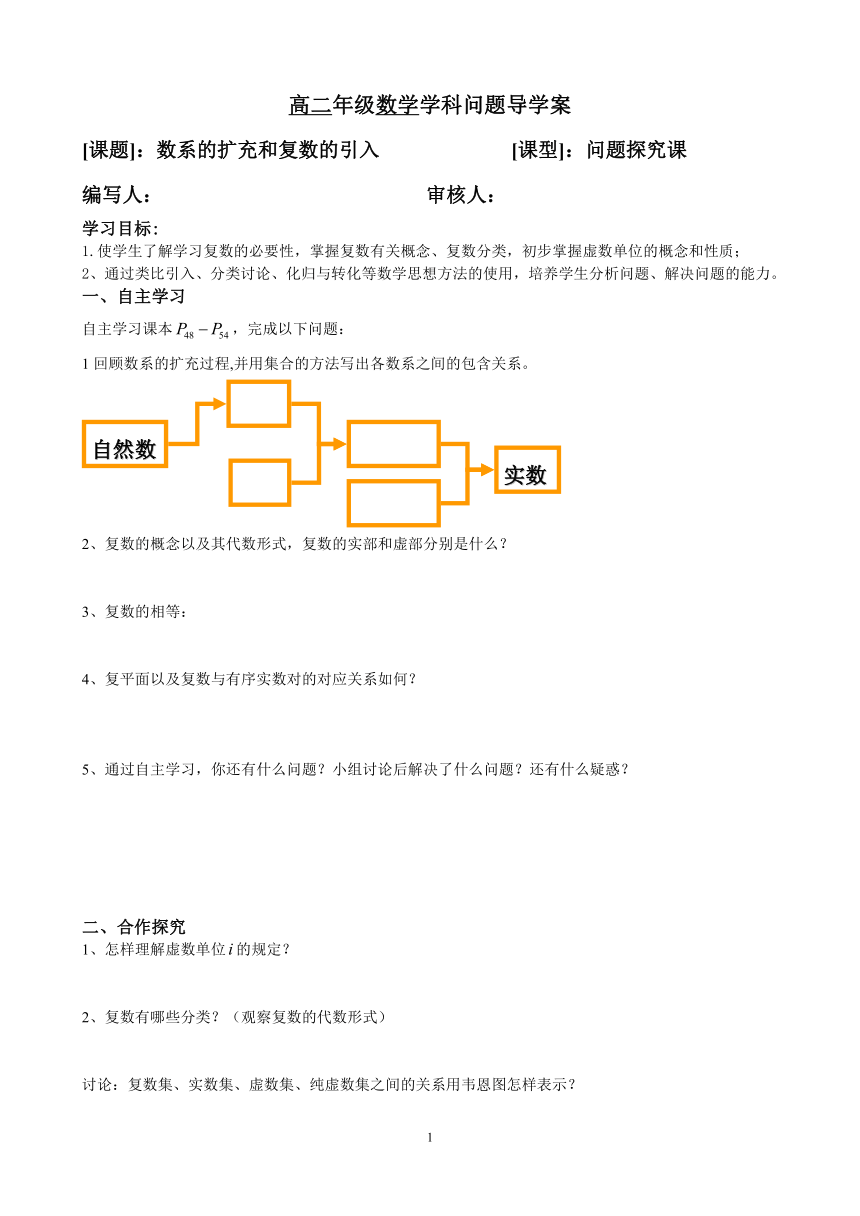
高二年级数学学科问题导学案
[课题]：数系的扩充和复数的引入 [课型]：问题探究课
编写人： 审核人：
学习目标:
1.使学生了解学习复数的必要性，掌握复数有关概念、复数分类，初步掌握虚数单位的概念和性质；
2、通过类比引入、分类讨论、化归与转化等数学思想方法的使用，培养学生分析问题、解决问题的能力。
一、自主学习
自主学习课本，完成以下问题：
1回顾数系的扩充过程,并用集合的方法写出各数系之间的包含关系。
2、复数的概念以及其代数形式，复数的实部和虚部分别是什么？
3、复数的相等：
4、复平面以及复数与有序实数对的对应关系如何？
5、通过自主学习，你还有什么问题？小组讨论后解决了什么问题？还有什么疑惑？
二、合作探究
1、怎样理解虚数单位的规定？
2、复数有哪些分类？（观察复数的代数形式）
讨论：复数集、实数集、虚数集、纯虚数集之间的关系用韦恩图怎样表示？
3、两个复数可以比较大小吗？
思考：两个复数相等的充要条件是什么？
4、类比实数的几何意义，复数的几何意义是什么？
三、典型例题
例1、实数m取什么值时，复数
（1）实数？ （2）虚数？（3）纯虚数？
[强化训练]当m为何实数时，复数是
（1）实数 （2）虚数 （3）纯虚数（4）零
反思：复数成为实数、虚数、纯虚数、零的充要条件是什么？
例2：已知求x与y？
反思：复数相等的充要条件；该题采用什么思想方法？
例3：设
若z是虚数，求m的取值范围
若以复数z的实部、虚部为横、纵坐标的点在第三象限，求m的取值范围
（3）若z〉0，求m的取值范围
反思：虚数和纯虚数的关系？什么条件下，复数可以比较大小？该题采用什么思想方法？
例4：已知集合若求实数m的值？
反思：集合元素的特征？该题采用什么思想方法？
四、反思总结
本节课你有什么收获？小组交流一下。
五、当堂检测
1． m∈R，复数z=（m-2）(m+5)+(m-2)（m-5）i，则z为纯虚数的充要条件是m的值为 ( )
A.2或5 B.5 C.2或-5 D.-5
2．实数，满足，则的值是（　　）
Ａ．1 Ｂ．2 Ｃ． Ｄ．
3. 实数m分别取什么值时，复数z＝m2+m-2＋(m2-1)i是
(1)实数？ (2)虚数？ (3)纯虚数？
4. 设则的关系是( )
A． B． C． D．无法确定
自然数
实数
PAGE
1