人教版数学七年级上册同步课时练习:4.3.3 余角和补角 (word版含答案)
文档属性
| 名称 | 人教版数学七年级上册同步课时练习:4.3.3 余角和补角 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 219.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-15 11:50:37 | ||
图片预览


文档简介
4.3.3 余角和补角
知识点 1 余角和补角的概念
1.若∠α与∠β互为余角,则( )
A.∠α+∠β=180° B.∠α-∠β=180°
C.∠α-∠β=90° D.∠α+∠β=90°
2.下列角的图示中,可能与30°角互补的是( )
3.[2020·陕西] 若∠A=23°,则∠A余角的大小是( )
A.57° B.67° C .77° D.157°
4.下列叙述正确的是( )
A.180°的角是补角
B.110°的角和90°的角互为补角
C.10°的角,20°的角,60°的角互为余角
D.120°的角和60°的角互为补角
5.互为余角且相等的角的度数都是 ,互为补角且相等的角的度数都是 .
6.[教材练习第3题变式] 一个角的补角比它的余角的3倍小20°,求这个角的度数.
知识点 2 余角和补角的性质
7.若∠1与∠2互补,∠2与∠3互补,∠1=50°,则∠3等于( )
A.50° B.130° C.40° D.140°
8.已知∠1+∠2=90°,∠3+∠4=90°,如果∠1=∠3,那么∠2=∠4,依据是( )
A.同角的余角相等 B.同角的补角相等
C.等角的余角相等 D.等角的补角相等
9.将两个能完全重合的三角板如图放置(即两个直角顶点重合),我们可得∠α=∠β,其中的道理是 .
10.如图,O是直线AB上一点,OC平分∠BOD,OE平分∠AOD,则与∠COD互余的角是 .
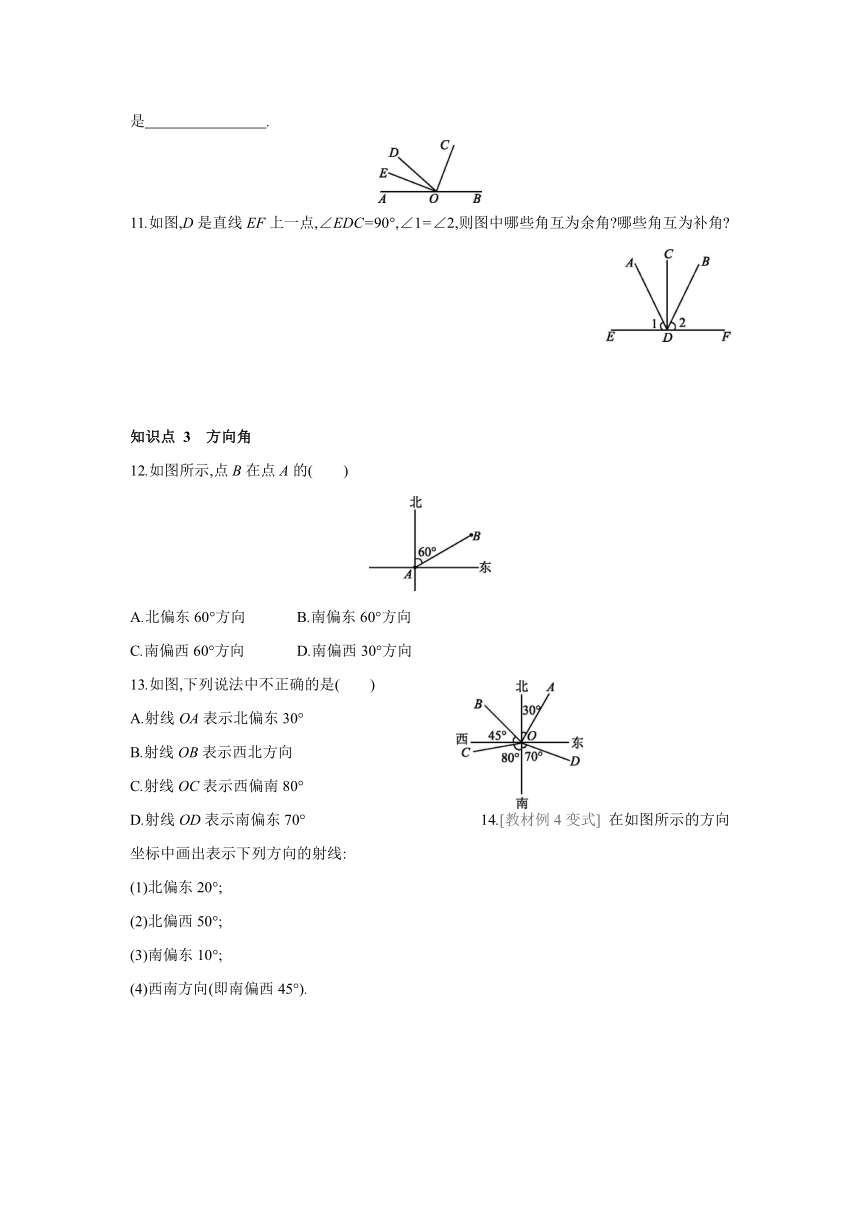
11.如图,D是直线EF上一点,∠EDC=90°,∠1=∠2,则图中哪些角互为余角 哪些角互为补角
知识点 3 方向角
12.如图所示,点B在点A的( )
A.北偏东60°方向 B.南偏东60°方向
C.南偏西60°方向 D.南偏西30°方向
13.如图,下列说法中不正确的是( )
A.射线OA表示北偏东30°
B.射线OB表示西北方向
C.射线OC表示西偏南80°
D.射线OD表示南偏东70° 14.[教材例4变式] 在如图所示的方向坐标中画出表示下列方向的射线:
(1)北偏东20°;
(2)北偏西50°;
(3)南偏东10°;
(4)西南方向(即南偏西45°).
15.一个锐角的余角比它的补角( )
A.相等 B.小90°
C.大90° D.不能确定大小
16.点A,B,C,D,E的位置如图所示,则下列结论中正确的是( )
A.∠AOB=130°
B.∠AOB=∠DOE
C.∠COD与∠BOE互补
D.∠AOB与∠COD互余
17.如图所示,A地和B地都是海上观测站,B地在A地的正东方向,从A地发现它的北偏东60°方向有一不明物体,同时,从B地发现这个不明物体在它的北偏东30°方向,试在图中确定这个不明物体的位置.
18.如图,OD平分∠BOC,OE平分∠AOC.若∠BOC=70°,∠AOC=50°,请求出∠AOB与∠DOE的度数,并判断它们是否互补.
19.如图,直线AB,CD相交于点O,OF平分∠AOE,∠DOF=90°.
(1)写出图中所有与∠AOD互补的角;
(2)若∠AOE=120°,求∠BOD的度数.
20.如图,先找到长方形纸片ABCD的宽DC的中点E,将∠C过点E折起任意一个角,折痕是EF,点C落在点C'处,再将∠D过点E折起,使DE和C'E重合,折痕是GE,请探索下列问题:
(1)∠FEC'和∠GEC'互为余角吗 为什么
(2)在上述图形中,还有哪些角互为余角(至少再写出五组)
答案
1.D 2.D
3.B 因为∠A=23°,所以∠A的余角是90°-23°=67°.故选B.
4.D A不正确,互补是指两个角的和为180°;B不正确,110°+90°=200°>180°;C不正确,这里有三个角.
5.45° 90°
6.解:设这个角的度数为x°.
由题意,得180-x=3(9,
解得x=35.
答:这个角的度数为35°.
7.A 因为∠1+∠2=180°,∠2+∠3=180°,所以∠3=∠1=50°.故选A.
8.C
9.同角的余角相等
10.∠DOE,∠AOE 因为∠AOD+∠BOD=180°,OC平分∠BOD,OE平分∠AOD,
所以∠DOE+∠COD=90°,∠DOE=∠AOE.所以与∠COD互余的角是∠DOE和∠AOE.
11.解:∠1与∠ADC,∠1与∠BDC,∠2与∠BDC,∠2与∠ADC互为余角;
∠1与∠ADF,∠2与∠ADF,∠2与∠BDE,∠1与∠BDE,∠EDC与∠FDC互为补角.
12.A
13.C
14.解:(1)(2)(3)(4)如图所示.
15.B
16.C 因为∠AOB=50°,∠DOE=40°,所以选项A,B错误.
因为∠COE=90°,所以∠COD=∠COE-∠DOE=90°-40°=50°.所以∠AOB=∠COD,所以选项D错误.
因为∠BOE=130°,∠COD=50°,所以∠COD+∠BOE=50°+130°=180°.所以选项C正确.
17.解:如图所示,图中点C即为不明物体的位置.
18.解:因为OD平分∠BOC,∠BOC=70°,
所以∠COD=∠BOC=×70°=35°.
因为OE平分∠AOC,∠AOC=50°,
所以∠COE=∠AOC=×50°=25°.
所以∠DOE=∠COD+∠COE=35°+25°=60°.
因为∠BOC=70°,∠AOC=50°,
所以∠AOB=∠BOC+∠AOC=70°+50°=120°.
所以∠AOB+∠DOE=120°+60°=180°.所以∠AOB与∠DOE互补.
19.解:(1)因为直线AB,CD相交于点O,
所以∠AOC和∠BOD均与∠AOD互补.
因为OF平分∠AOE,
所以∠AOF=∠EOF.
因为∠DOF=90°,
所以∠COF=∠DOF=90°.
所以∠DOE=∠AOC.
所以∠DOE也是∠AOD的补角.
所以与∠AOD互补的角有∠AOC,∠BOD,∠DOE.
(2)因为OF平分∠AOE,∠AOE=120°,
所以∠EOF=∠AOE=60°.
因为∠DOF=90°,
所以∠DOE=∠DOF-∠EOF=90°-60°=30°.
所以∠BOD=180°-∠AOE-∠DOE=30°.
20.解:(1)∠FEC'和∠GEC'互为余角.
理由:由折纸过程,知∠CEF=∠FEC',∠DEG=∠GEC'.
因为∠FEC'+∠GEC'+∠CEF+∠DEG=180°,
所以∠FEC'+∠GEC'=90°.
故∠FEC'和∠GEC'互为余角.
(2)答案不唯一,如∠FEC'与∠DEG,∠CEF与∠GEC',∠CEF与∠DEG,∠FEC'与∠EFC',∠CEF与∠EFC',∠FEC'与∠EFC,∠CEF与∠EFC,∠GEC'与∠EGC',∠DEG与∠EGC',∠DEG与∠EGD,∠GEC'与∠EGD等互为余角.
知识点 1 余角和补角的概念
1.若∠α与∠β互为余角,则( )
A.∠α+∠β=180° B.∠α-∠β=180°
C.∠α-∠β=90° D.∠α+∠β=90°
2.下列角的图示中,可能与30°角互补的是( )
3.[2020·陕西] 若∠A=23°,则∠A余角的大小是( )
A.57° B.67° C .77° D.157°
4.下列叙述正确的是( )
A.180°的角是补角
B.110°的角和90°的角互为补角
C.10°的角,20°的角,60°的角互为余角
D.120°的角和60°的角互为补角
5.互为余角且相等的角的度数都是 ,互为补角且相等的角的度数都是 .
6.[教材练习第3题变式] 一个角的补角比它的余角的3倍小20°,求这个角的度数.
知识点 2 余角和补角的性质
7.若∠1与∠2互补,∠2与∠3互补,∠1=50°,则∠3等于( )
A.50° B.130° C.40° D.140°
8.已知∠1+∠2=90°,∠3+∠4=90°,如果∠1=∠3,那么∠2=∠4,依据是( )
A.同角的余角相等 B.同角的补角相等
C.等角的余角相等 D.等角的补角相等
9.将两个能完全重合的三角板如图放置(即两个直角顶点重合),我们可得∠α=∠β,其中的道理是 .
10.如图,O是直线AB上一点,OC平分∠BOD,OE平分∠AOD,则与∠COD互余的角是 .
11.如图,D是直线EF上一点,∠EDC=90°,∠1=∠2,则图中哪些角互为余角 哪些角互为补角
知识点 3 方向角
12.如图所示,点B在点A的( )
A.北偏东60°方向 B.南偏东60°方向
C.南偏西60°方向 D.南偏西30°方向
13.如图,下列说法中不正确的是( )
A.射线OA表示北偏东30°
B.射线OB表示西北方向
C.射线OC表示西偏南80°
D.射线OD表示南偏东70° 14.[教材例4变式] 在如图所示的方向坐标中画出表示下列方向的射线:
(1)北偏东20°;
(2)北偏西50°;
(3)南偏东10°;
(4)西南方向(即南偏西45°).
15.一个锐角的余角比它的补角( )
A.相等 B.小90°
C.大90° D.不能确定大小
16.点A,B,C,D,E的位置如图所示,则下列结论中正确的是( )
A.∠AOB=130°
B.∠AOB=∠DOE
C.∠COD与∠BOE互补
D.∠AOB与∠COD互余
17.如图所示,A地和B地都是海上观测站,B地在A地的正东方向,从A地发现它的北偏东60°方向有一不明物体,同时,从B地发现这个不明物体在它的北偏东30°方向,试在图中确定这个不明物体的位置.
18.如图,OD平分∠BOC,OE平分∠AOC.若∠BOC=70°,∠AOC=50°,请求出∠AOB与∠DOE的度数,并判断它们是否互补.
19.如图,直线AB,CD相交于点O,OF平分∠AOE,∠DOF=90°.
(1)写出图中所有与∠AOD互补的角;
(2)若∠AOE=120°,求∠BOD的度数.
20.如图,先找到长方形纸片ABCD的宽DC的中点E,将∠C过点E折起任意一个角,折痕是EF,点C落在点C'处,再将∠D过点E折起,使DE和C'E重合,折痕是GE,请探索下列问题:
(1)∠FEC'和∠GEC'互为余角吗 为什么
(2)在上述图形中,还有哪些角互为余角(至少再写出五组)
答案
1.D 2.D
3.B 因为∠A=23°,所以∠A的余角是90°-23°=67°.故选B.
4.D A不正确,互补是指两个角的和为180°;B不正确,110°+90°=200°>180°;C不正确,这里有三个角.
5.45° 90°
6.解:设这个角的度数为x°.
由题意,得180-x=3(9,
解得x=35.
答:这个角的度数为35°.
7.A 因为∠1+∠2=180°,∠2+∠3=180°,所以∠3=∠1=50°.故选A.
8.C
9.同角的余角相等
10.∠DOE,∠AOE 因为∠AOD+∠BOD=180°,OC平分∠BOD,OE平分∠AOD,
所以∠DOE+∠COD=90°,∠DOE=∠AOE.所以与∠COD互余的角是∠DOE和∠AOE.
11.解:∠1与∠ADC,∠1与∠BDC,∠2与∠BDC,∠2与∠ADC互为余角;
∠1与∠ADF,∠2与∠ADF,∠2与∠BDE,∠1与∠BDE,∠EDC与∠FDC互为补角.
12.A
13.C
14.解:(1)(2)(3)(4)如图所示.
15.B
16.C 因为∠AOB=50°,∠DOE=40°,所以选项A,B错误.
因为∠COE=90°,所以∠COD=∠COE-∠DOE=90°-40°=50°.所以∠AOB=∠COD,所以选项D错误.
因为∠BOE=130°,∠COD=50°,所以∠COD+∠BOE=50°+130°=180°.所以选项C正确.
17.解:如图所示,图中点C即为不明物体的位置.
18.解:因为OD平分∠BOC,∠BOC=70°,
所以∠COD=∠BOC=×70°=35°.
因为OE平分∠AOC,∠AOC=50°,
所以∠COE=∠AOC=×50°=25°.
所以∠DOE=∠COD+∠COE=35°+25°=60°.
因为∠BOC=70°,∠AOC=50°,
所以∠AOB=∠BOC+∠AOC=70°+50°=120°.
所以∠AOB+∠DOE=120°+60°=180°.所以∠AOB与∠DOE互补.
19.解:(1)因为直线AB,CD相交于点O,
所以∠AOC和∠BOD均与∠AOD互补.
因为OF平分∠AOE,
所以∠AOF=∠EOF.
因为∠DOF=90°,
所以∠COF=∠DOF=90°.
所以∠DOE=∠AOC.
所以∠DOE也是∠AOD的补角.
所以与∠AOD互补的角有∠AOC,∠BOD,∠DOE.
(2)因为OF平分∠AOE,∠AOE=120°,
所以∠EOF=∠AOE=60°.
因为∠DOF=90°,
所以∠DOE=∠DOF-∠EOF=90°-60°=30°.
所以∠BOD=180°-∠AOE-∠DOE=30°.
20.解:(1)∠FEC'和∠GEC'互为余角.
理由:由折纸过程,知∠CEF=∠FEC',∠DEG=∠GEC'.
因为∠FEC'+∠GEC'+∠CEF+∠DEG=180°,
所以∠FEC'+∠GEC'=90°.
故∠FEC'和∠GEC'互为余角.
(2)答案不唯一,如∠FEC'与∠DEG,∠CEF与∠GEC',∠CEF与∠DEG,∠FEC'与∠EFC',∠CEF与∠EFC',∠FEC'与∠EFC,∠CEF与∠EFC,∠GEC'与∠EGC',∠DEG与∠EGC',∠DEG与∠EGD,∠GEC'与∠EGD等互为余角.
