必修第二册9.2用样本估计总体 同步练习(Word版含解析)
文档属性
| 名称 | 必修第二册9.2用样本估计总体 同步练习(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 788.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-14 00:00:00 | ||
图片预览


文档简介
人教A版(2019)必修第二册 9.2 用样本估计总体 同步练习
一、单选题
1.我们正处于一个大数据飞速发展的时代,对于大数据人才的需求也越来越大,大数据的相关岗位大致可分为四类:数据开发、数据分析、数据挖掘、数据产品.某市2019年这几类工作岗位的薪资(单位:万元/月)情况如下表所示:
数据开发 8% 25% 32% 35%
数据分析 15% 36% 32% 17%
数据挖掘 9% 12% 28% 51%
数据产品 7% 17% 41% 35%
由表中数据可得该市大数据相关的各类岗位的薪资水平高低情况为( )A.数据挖掘>数据开发>数据产品>数据分析 B.数据挖掘>数据产品>数据开发>数据分析
C.数据挖掘>数据开发>数据分析>数据产品 D.数据挖掘>数据产品>数据分析>数据开发
2.已知某7个数的平均数为4,方差为2,现加入一个新数据4,此时这8个数的平均数为,方差为,则( )
A., B.,
C., D.,
3.某赛季甲乙两名篮球运动员在若干场比赛中的得分情况如下:
甲:21、22、23、25、28、29、30、30;
乙:14、16、23、26、28、30、33、38.
则下列描述合理的是( )
A.甲队员每场比赛得分的平均值大 B.乙队员每场比赛得分的平均值大
C.甲队员比赛成绩比较稳定 D.乙队员比赛成绩比较稳定
4.已知甲 乙 丙 丁 戊五位同学高一入学时年龄的平均数 中位数均为16,方差为0.8,则三年后,下列判断错误的是( )
A.这五位同学年龄的平均数变为19 B.这五位同学年龄的中位数变为19
C.这五位同学年龄的方差仍为0.8 D.这五位同学年龄的方差变为3.8
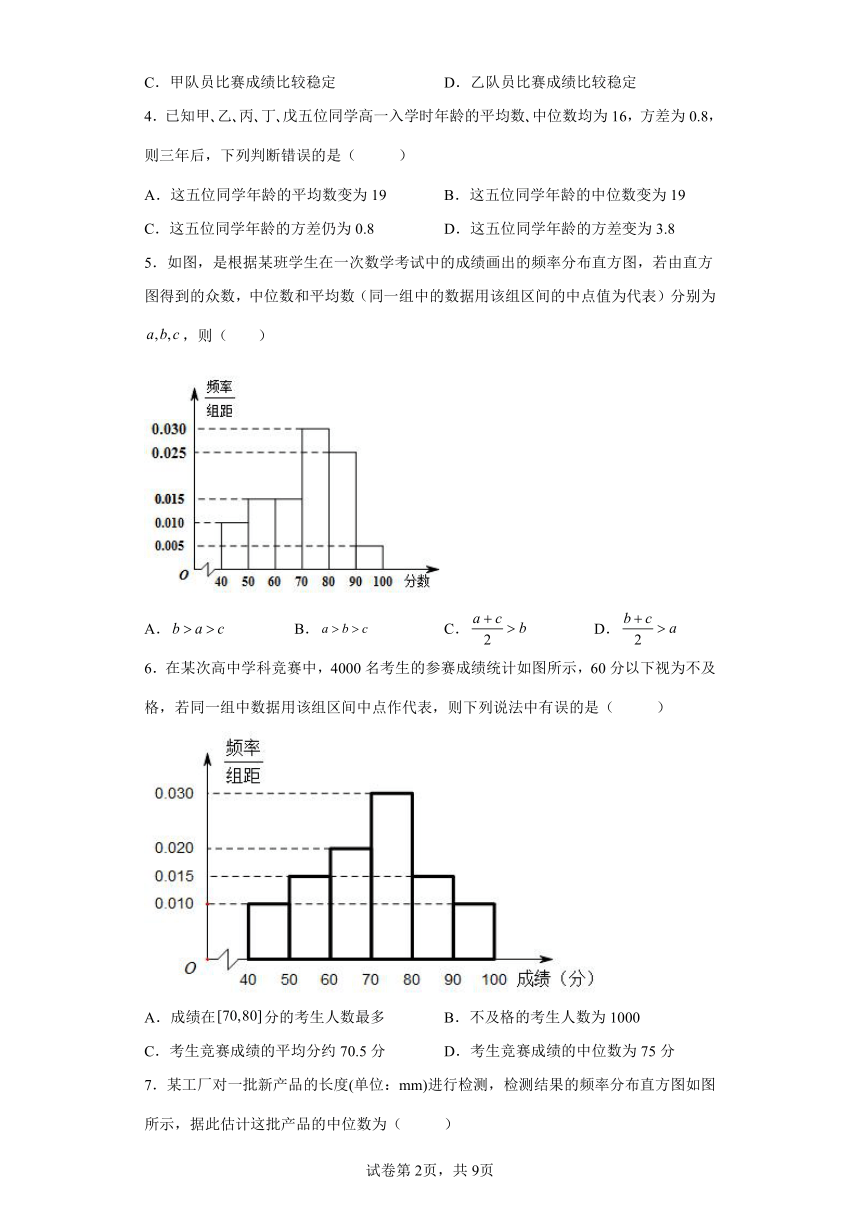
5.如图,是根据某班学生在一次数学考试中的成绩画出的频率分布直方图,若由直方图得到的众数,中位数和平均数(同一组中的数据用该组区间的中点值为代表)分别为,则( )
A. B. C. D.
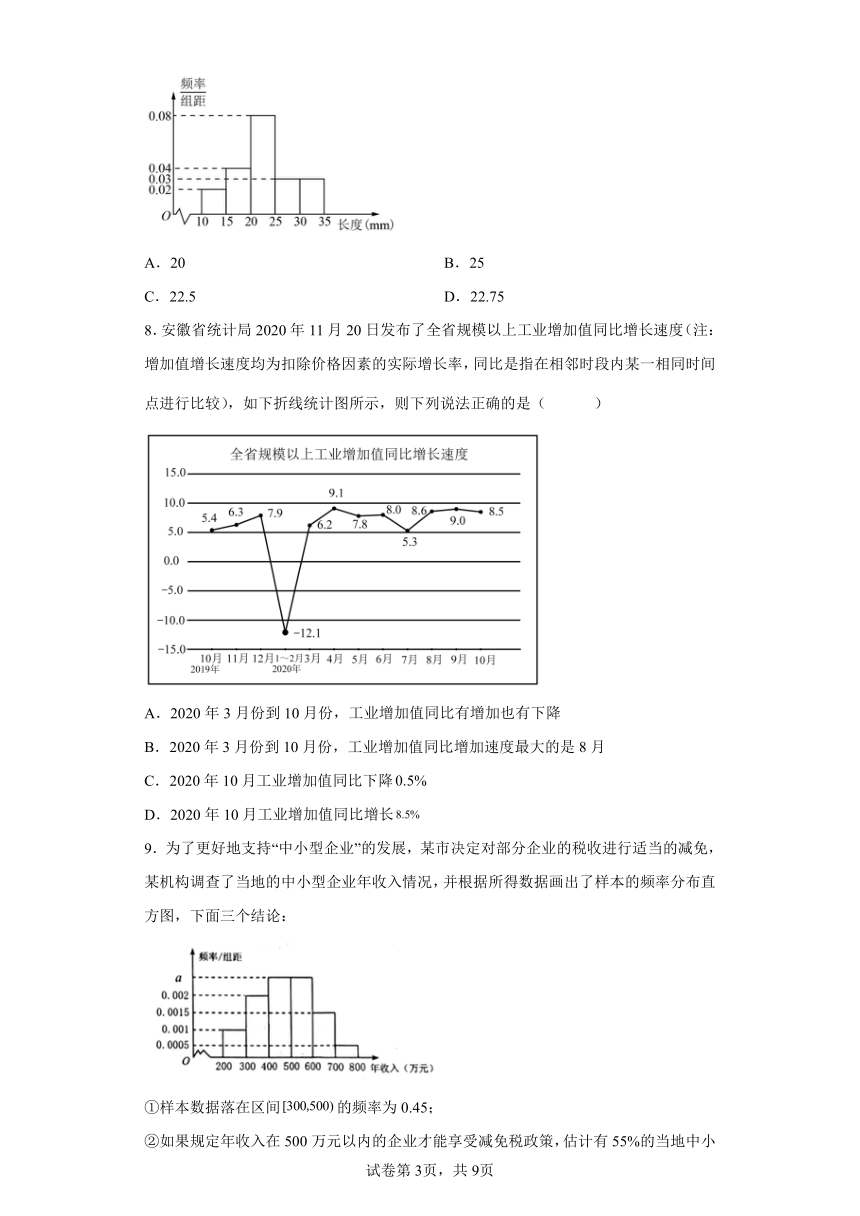
6.在某次高中学科竞赛中,4000名考生的参赛成绩统计如图所示,60分以下视为不及格,若同一组中数据用该组区间中点作代表,则下列说法中有误的是( )
A.成绩在分的考生人数最多 B.不及格的考生人数为1000
C.考生竞赛成绩的平均分约70.5分 D.考生竞赛成绩的中位数为75分
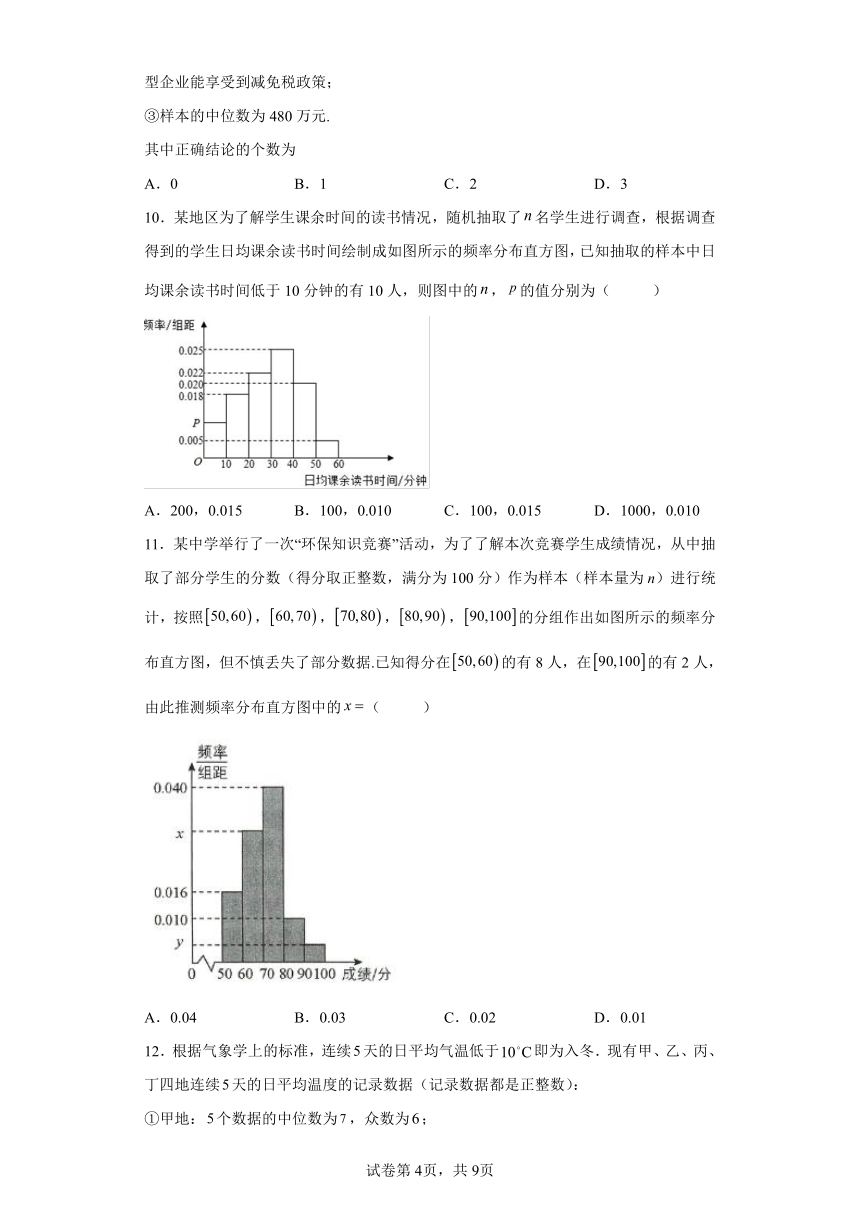
7.某工厂对一批新产品的长度(单位:mm)进行检测,检测结果的频率分布直方图如图所示,据此估计这批产品的中位数为( )
A.20 B.25
C.22.5 D.22.75
8.安徽省统计局2020年11月20日发布了全省规模以上工业增加值同比增长速度(注:增加值增长速度均为扣除价格因素的实际增长率,同比是指在相邻时段内某一相同时间点进行比较),如下折线统计图所示,则下列说法正确的是( )
A.2020年3月份到10月份,工业增加值同比有增加也有下降
B.2020年3月份到10月份,工业增加值同比增加速度最大的是8月
C.2020年10月工业增加值同比下降
D.2020年10月工业增加值同比增长
9.为了更好地支持“中小型企业”的发展,某市决定对部分企业的税收进行适当的减免,某机构调查了当地的中小型企业年收入情况,并根据所得数据画出了样本的频率分布直方图,下面三个结论:
①样本数据落在区间的频率为0.45;
②如果规定年收入在500万元以内的企业才能享受减免税政策,估计有55%的当地中小型企业能享受到减免税政策;
③样本的中位数为480万元.
其中正确结论的个数为
A.0 B.1 C.2 D.3
10.某地区为了解学生课余时间的读书情况,随机抽取了名学生进行调查,根据调查得到的学生日均课余读书时间绘制成如图所示的频率分布直方图,已知抽取的样本中日均课余读书时间低于10分钟的有10人,则图中的,的值分别为( )
A.200,0.015 B.100,0.010 C.100,0.015 D.1000,0.010
11.某中学举行了一次“环保知识竞赛”活动,为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本量为n)进行统计,按照,,,,的分组作出如图所示的频率分布直方图,但不慎丢失了部分数据.已知得分在的有8人,在的有2人,由此推测频率分布直方图中的( )
A.0.04 B.0.03 C.0.02 D.0.01
12.根据气象学上的标准,连续天的日平均气温低于即为入冬.现有甲、乙、丙、丁四地连续天的日平均温度的记录数据(记录数据都是正整数):
①甲地:个数据的中位数为,众数为;
②乙地:个数据的平均数为,极差为;
③丙地:个数据的平均数为,中位数为;
④丁地:个数据的平均数为,方差小于.
则肯定进入冬季的地区是( )
A.甲地 B.乙地 C.丙地 D.丁地
13.甲、乙、丙三名射箭运动员在某次测试中各射箭20次,三人的测试成绩如下表:分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则有( )
甲的成绩
环数 7 8 9 10
频数 5 5 5 5
乙的成绩
环数 7 8 9 10
频数 6 4 4 6
丙的成绩
环数 7 8 9 10
频数 4 6 6 4
A. B. C. D.
14.如图是某地某月1日至15日的日平均温度变化的折线图,根据该折线图,下列结论正确的是( )
A.由折线图能预测16日温度要低于19℃
B.这15天日平均温度的极差为18℃
C.连续三天日平均温度的方差最大的是7日,8日,9日三天
D.由折线图能预测本月温度小于25℃的天数少于温度大于25℃的天数
15.抽样统计甲射击运动员10次的训练成绩分别为86,85,88,86,90,89,88,87,85,92,则这10次成绩的80%分位数为( )
A.88.5 B.89 C.91 D.89.5
二、填空题
16.若一组数据为82,81,79,78,95,88,92,84,则该组数据的75%分位数是___________.
17.下图是国家统计局发布的2020年2月至2021年2月全国居民消费价格涨跌幅折线图;则给出下列三个结论:①2020年11月居民消费价格低于2019年同期;②2020年3月至7月居民的消费价格持续增长;③2020年7月的消费价格低于2020年3月的消费价格.其中所有正确结论的序号是________.
说明:1.在统计学中,同比是指本期统计数据与上一年同期统计数据相比较,例如年2月与2020年2月相比较;环比是指本期统计数据与上期统计数据相比较,例如2020年4月与年3月相比较.
2.同比增长率=,环比增长率=.
18.下图是国家统计局发布的2020年2月至2021年2月全国居民消费价格涨跌幅折线图.
说明:(1)在统计学中,同比是指本期统计数据与上一年同期统计数据相比较,例如2021年2月与2020年2月相比较:环比是指本期统计数据与上期统计数据相比较,例如2020年4月与2020年3月相比较.
(2)同比增长率环比增长率.
给出下列四个结论:
①2020年11月居民消费价格低于2019年同期;
②2020年3月至7月居民的消费价格持续增长;
③2020年3月的消费价格低于2020年4月的消费价格;
④2020年7月的消费价格低于2020年3月的消费价格.
其中所正确结论的序号是____________.
三、解答题
19.有20种不同的零食,每100g可食部分包含的能量(单位:kJ)如下:
110 120 123 165 432 190 174 235 428 318
249 280 162 146 210 120 123 120 150 140
(1)以上述20个数据组成总体,求总体平均数与总体标准差
(2)设计恰当的随机抽样方法,从总体中抽取一个容量为7的样本.
(3)利用上面的抽样方法,再抽取容量为7的样本,这个样本的平均数和标准差与(2)中的结果一样吗?为什么?
(4)利用(2)中的随机抽样方法,分别从总体中抽取一个容量为10,13,16,19的样本,分析样本容量与样本的平均数和标准差对总体的估计效果之间有什么关系.
20.在技术人员的指导下,某棉花种植基地的棉花产量和质量均有大幅度地提升,已知该棉花种植基地今年产量为,技术人员随机抽取了棉花,测量其马克隆值(棉花的马克隆值是反映棉花纤维细度与成熟度的综合指标,是棉纤维重要的内在质量指标之一,与棉花价格关系密切),得到如下统计表及不完整的频率分布直方图.
马克隆值
质量/ t 0.04 0.06 0.12 0.16 b a 0.06 0.03 0.01
(1)求表中的值,并补全频率分布直方图;
(2)根据频率分布直方图,估计样本的马克隆值的众数及中位数;
(3)根据马克隆值可将棉花分为三个等级,不同等级的棉花价格如下表所示:
马克隆值 或
级别
价格(万元/t) 1.6 1.52 1.44
用样本估计总体,估计该棉花种植基地今年的总产值.
21.为研究某植物园中某类植物的高度,随机抽取了高度在(单位:)的50株植物,得到其高度的频率分布直方图(如图所示).
(1)求的值;
(2)若园内有该植物1000株,试根据直方图信息估计高度在的植物数量.
22.某地区拟举办汉字听写大赛,某校为了选拔优秀的学生参加比赛,在本校举行了次汉字听写大赛,其中甲、乙两位同学的成绩最优异,由甲、乙两位同学的成绩绘制的茎叶图如图所示.已知甲成绩的中位数小于乙成绩的中位数.
(1)求的值;
(2)若要从甲、乙中选择一名同学参加该地区举办的汉字听写大赛,试从统计学的角度分析,选哪位同学比较合适.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
根据题意和表格的数据分别计算数据开发、数据分析、数据产品的平均薪资,进而比较大小即可.
【详解】
由题中选项知数据挖掘的平均薪资最高,故只需计算并比较其他三类工作岗位的平均薪资.估计数据开发的平均薪资为;
估计数据分析的平均薪资为;
估计数据产品的平均薪资为.
故数据挖掘>数据产品>数据开发>数据分析.
故选:B.
2.A
由题设条件,利用平均数和方差的计算公式计算即可求解.
【详解】
设7个数为,
则,
,
所以,
所以,
则这个数的平均数为,
方差为.
故选:A.
3.C
计算均值,再根据数据的集中度判断.
【详解】
甲的均值为,
乙的均值为,
两者均值相同,甲的方差为
乙的方差为
,
甲的方差小于乙的方差,甲稳定.
故选:C.
4.D
利用平均数、中位数、方差的定义直接求解.
【详解】
甲、乙、丙、丁、戊五位同学高一入学时年龄的平均数、中位数均为16,方差位0.8,
三年后,
这五位同学年龄的平均数变为16+3=19,故A正确;
这五位同学年龄的中位数变为16+3=19,故B正确;
这五位同学的方差不变,仍为0.8,故C正确,D错误.
故选:D.
5.B
根据频率分布直方图读出众数a,计算中位数b,平均数c,再比较大小.
【详解】
由频率分布直方图可知:众数;
中位数应落在70-80区间内,则有:,解得:;
平均数
=4.5+8.25+9.75+22.5+21.25+4.75=71
所以
故选:B
从频率分布直方图可以估计出的几个数据:
(1)众数:频率分布直方图中最高矩形的底边中点的横坐标;
(2)平均数:频率分布直方图每组数值的中间值乘以频率后相加;
(3)中位数:把频率分布直方图分成两个面积相等部分的平行于y轴的直线横坐标.
6.D
用频率分布直方图的相关知识和公式逐一计算验证选项.
【详解】
由频率分布直方图可得,成绩在的频率最高,因此考生人数最多,故A正确;
由频率分布直方图可得,成绩在的频率为,因此,不及格的人数为,故B正确;
由频率分布直方图可得:平均分等于,故C正确;
因为成绩在的频率为,由的频率为,所以中位数为,故D错误.
故选D.
本题考查频率分布直方图的众数、中位数、平均数以及样本容量的求法,考查学生的计算能力,熟记公式是解题的关键,属于中档题.
7.C
根据频率分布直方图,计算出频率为0.5时落在的组,0.5减去前几组的频率的差,再根据小长方形的面积可得出答案.
【详解】
由频率分布直方图得,第一组、第二组的频率为,
第三组的频率为,所以中位数落在第三组并设为,
则有,解得.
故选:C.
8.D
A.增长速度都是正值,工业增加值都在增加
B.可看到,最高点是在四月
C. 2020年10月工业增加值同比增长
【详解】
由题意可知该折线统计图是工业增加值同比增长率,2020年3月份到10月份,工业增加值同比都在增加,故A错误;
2020年3月份到10月份,工业增加值同比增加速度最大的是4月,增速为,故B错误;
2020年10月工业增加值同比增长,故C错误,D正确.
故选:D
9.D
根据直方图求出,求出的频率,可判断①;求出的频率,可判断②;根据中位数是从左到右频率为的分界点,先确定在哪个区间,再求出占该区间的比例,求出中位数,判断③.
【详解】
由,,
的频率为,①正确;
的频率为,②正确;
的频率为,的频率为,
中位数在且占该组的,
故中位数为,③正确.
故选:D.
本题考查补全直方图,由直方图求频率和平均数,属于基础题
10.B
根据频率分布直方图,由频率之和为1,列出方程即可求出;根据日均课余读书时间低于10分钟的人数,及其对应的频率,即可求出.
【详解】
利用频率之和为1可得,,解得,
根据频率、频数、样本容量之间关系可得,,解得.
故选:B.
11.B
根据频率分布直方图,先求得抽取学生的人数.
【详解】
得分在的有8人, 得分在的频率为
所以抽取中的人数为人
在的有2人,所以在的频率为,所以
∴由频率分布直方图各小矩形面积和为1,得.
解得.
故选:B.
本题考查了频率分布直方图的意义,补全频率分布直方图,属于基础题.
12.D
根据各地连续天的日平均温度的记录数据,通过特殊值法,可排除ABC选项;根据方差的计算公式,结合丁地的气温数据,可判断D正确.
【详解】
①甲地:个数据的中位数为,众数为;则这个数据可能为,,,,;即连续天的日平均气温不是都低于,所以甲地不一定入冬,故A错;
②乙地:个数据的平均数为,极差为;则这个数据可能为,,,,;即连续天的日平均气温不是都低于,所以乙地不一定入冬,故B错;
③丙地:个数据的平均数为,中位数为;则这个数据可能为,,,,;即连续天的日平均气温不是都低于,所以丙地不一定入冬,故C错;
④丁地:个数据的平均数为,方差小于.如有数据大于等于,则方差必大于等于,不满足题意,因此丁地这续天的日平均气温都低于,所以丁地一定入冬,故D正确;
故选:D.
13.B
分别根据平均数和方差公式,计算结果.
【详解】
,
,
,
,
,
,
由,得.
故选:B
结论点睛:本题考查平均数和方差的计算,
1.平均数
2.方差,
3.标准差,
4.平均数大说明样本的平均水平高,方差和标准差大说明样本比较分散,与平均水平差距较大,不稳定.
14.C
根据图象中的信息,逐个选项分析处理即可.
【详解】
A选项,由折线图无法预测16日温度要是否低于19℃,故A错误;
B选项,这15天日平均温度的极差为19℃,B错误;
C选项,日平均温度的方差的大小取决于日平均温度的波动的大小,7,8,9三日的日平均温度的波动最大,故日平均温度的方差最大,C正确;
D选项,由折线图无法预测本月温度小于19℃的天数是否少于温度大于25℃的天数,故D错误.
故选:C.
15.D
将数据从小到大排列,计算,得到答案.
【详解】
甲射击运动员10次的训练成绩从小到大分别为:85,85,86,86,87,88,88,89,90,92.
,这10次成绩的80%分位数为:.
故选:D.
16.90
可得该组数据的75%分位数在第6位和第7位之间,求出平均值即可.
【详解】
由题可得一共有8个数据,则该组数据的75%分位数在第6位和第7位之间,为.
故答案为:90.
17.①③
根据题中数据,根据环比、同比增长率的概念,即可判断①②的正误;设2020年3月居民消费价格为,4月消费价格为,5月消费价格为,6月消费价格为,7月消费价格为,根据环比增长率的公式,即可求得与的关系,同理可求得与的关系,即可判断③的正误,即可得答案.
【详解】
对于①:由图可知2020年11月同比增长率为-0.5,由同比增长率的计算公式可得,2020年11月居民消费价格低于2019年同期,故①正确;
对于②:由图可知,2020年3月至6月的环比增长率为负,由环比增长率的计算公式可得消费价格下降,故②错误;
对于③:设2020年3月居民消费价格为,4月消费价格为,5月消费价格为,6月消费价格为,7月消费价格为,
由题意得:,解得,
,解得,
,解得,
,解得,
所以,
所以2020年7月消费价格低于2020年3月消费价格,故③正确.
故答案为:①③
18.①④
根据国居民消费价格涨跌幅折线图,结合题中说明和计算公式逐一判断即可.
【详解】
①:由国居民消费价格涨跌幅折线图可知:同比增长率为,由题中说明所给同比增长率定义可知:2020年11月居民消费价格低于2019年同期,故本结论正确;
②:由国居民消费价格涨跌幅折线图可知:2020年3月至6月环比增长率为负值,由题中所给的环比增长率定义可知:2020年3月至6月居民的消费价格持续下降,所以本结论不正确;
③:设2020年3月的消费价格为,2020年4月的消费价格为,
根据题中所给的环比增长率公式可得:,
所以,因此本结论不正确;
④:设2020年5月的消费价格为,2020年6月的消费价格为,2020年7月的消费价格为,
根据题中所给的环比增长率公式可得:
,,
,所以,因此本结论正确;
故答案为:①④
关键点睛:理解同比增长率、环比增长率的定义,运用同比增长率、环比增长率的公式进行解题是关键.
19.(1)平均数为199.75,总体标准差为95.26;(2)抓阄法;(3)(2)和(3)的计算结果不相同的概率相当大,而相同的概率很小;(4)由于样本的随机性,也有极个别(小概率)的例外情况.
(1)由平均数和方差公式计算;
(2)用抓阄法进行抽样;
(3)由于抽样的随机性,两种结果相同的概率很小,不同概率很大.
(4)由于样本容量增大,估计总体的精确程度会提高,效果更好(也有个别现象效果不好).
【详解】
(1)总体平均数为199.75.
总体标准差为95.26.
(2)可以使用抓阄法进行抽样.
(3)由样本的随机性,知(2)和(3)的计算结果不相同的概率相当大,而相同的概率很小.
(4)随着样本容量的增加,分别用样本平均数和样本标准差估计总体平均数和总体标准差的效果会越来越好(即精度会越来越高).但是由于样本的随机性,也有极个别(小概率)的例外情况.
本题考查用样本估计总体,样本容量越大时,估计效果可能会更好些.
20.(1),,频率分布直方图见解析;
(2)众数为,中位数为;
(3)万元.
(1)由频率分布直方图和统计表可计算求得,由此可补全频率分布直方图;
(2)由频率分布直方图估计众数和中位数的方法直接求解即可;
(3)计算求得样本的产值,进而可得今年的总产值.
(1)
由题中频率分布直方图知:;
由统计表得:,
解得:.
补全的频率分布直方图如图所示:
(2)
由频率分布直方图知:马克隆值落在区间内的频率最大,故众数为.
,,中位数在区间内,
中位数为.
(3)
样本的产值为(万元),
估计该棉花种植基地今年的总产值为(万元).
21.(1);(2)280.
频率分布直方图中矩形面积和为1可得的值;
算出高度落在的植物的频率可得.
【详解】
(1),
解得;
(2)高度落在的植物的频率为,
高度在的植物数量为株
此题为统计基础题,考查频率分布直方图的含义.
22.(1)0;(2)乙同学比较合适.
(1)由乙的中位数为91,甲的中位数(90+x)小于91得解;
(2)计算甲乙二人三次成绩的平均数、方差等特征数据,再分析选择.
【详解】
(1)由茎叶图可知,乙同学成绩的中位数为.
又由茎叶图可得甲同学成绩的中位数大于或等于,
且甲成绩的中位数小于乙成绩的中位数,所以甲同学成绩的中位数只能为,
故.
(2)甲同学成绩的平均数为,
乙同学成绩的平均数为,
所以甲、乙成绩的平均数相等.
甲同学成绩的方差,
乙同学成绩的方差,
,所以乙同学的成绩更稳定,选乙同学比较合适.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.我们正处于一个大数据飞速发展的时代,对于大数据人才的需求也越来越大,大数据的相关岗位大致可分为四类:数据开发、数据分析、数据挖掘、数据产品.某市2019年这几类工作岗位的薪资(单位:万元/月)情况如下表所示:
数据开发 8% 25% 32% 35%
数据分析 15% 36% 32% 17%
数据挖掘 9% 12% 28% 51%
数据产品 7% 17% 41% 35%
由表中数据可得该市大数据相关的各类岗位的薪资水平高低情况为( )A.数据挖掘>数据开发>数据产品>数据分析 B.数据挖掘>数据产品>数据开发>数据分析
C.数据挖掘>数据开发>数据分析>数据产品 D.数据挖掘>数据产品>数据分析>数据开发
2.已知某7个数的平均数为4,方差为2,现加入一个新数据4,此时这8个数的平均数为,方差为,则( )
A., B.,
C., D.,
3.某赛季甲乙两名篮球运动员在若干场比赛中的得分情况如下:
甲:21、22、23、25、28、29、30、30;
乙:14、16、23、26、28、30、33、38.
则下列描述合理的是( )
A.甲队员每场比赛得分的平均值大 B.乙队员每场比赛得分的平均值大
C.甲队员比赛成绩比较稳定 D.乙队员比赛成绩比较稳定
4.已知甲 乙 丙 丁 戊五位同学高一入学时年龄的平均数 中位数均为16,方差为0.8,则三年后,下列判断错误的是( )
A.这五位同学年龄的平均数变为19 B.这五位同学年龄的中位数变为19
C.这五位同学年龄的方差仍为0.8 D.这五位同学年龄的方差变为3.8
5.如图,是根据某班学生在一次数学考试中的成绩画出的频率分布直方图,若由直方图得到的众数,中位数和平均数(同一组中的数据用该组区间的中点值为代表)分别为,则( )
A. B. C. D.
6.在某次高中学科竞赛中,4000名考生的参赛成绩统计如图所示,60分以下视为不及格,若同一组中数据用该组区间中点作代表,则下列说法中有误的是( )
A.成绩在分的考生人数最多 B.不及格的考生人数为1000
C.考生竞赛成绩的平均分约70.5分 D.考生竞赛成绩的中位数为75分
7.某工厂对一批新产品的长度(单位:mm)进行检测,检测结果的频率分布直方图如图所示,据此估计这批产品的中位数为( )
A.20 B.25
C.22.5 D.22.75
8.安徽省统计局2020年11月20日发布了全省规模以上工业增加值同比增长速度(注:增加值增长速度均为扣除价格因素的实际增长率,同比是指在相邻时段内某一相同时间点进行比较),如下折线统计图所示,则下列说法正确的是( )
A.2020年3月份到10月份,工业增加值同比有增加也有下降
B.2020年3月份到10月份,工业增加值同比增加速度最大的是8月
C.2020年10月工业增加值同比下降
D.2020年10月工业增加值同比增长
9.为了更好地支持“中小型企业”的发展,某市决定对部分企业的税收进行适当的减免,某机构调查了当地的中小型企业年收入情况,并根据所得数据画出了样本的频率分布直方图,下面三个结论:
①样本数据落在区间的频率为0.45;
②如果规定年收入在500万元以内的企业才能享受减免税政策,估计有55%的当地中小型企业能享受到减免税政策;
③样本的中位数为480万元.
其中正确结论的个数为
A.0 B.1 C.2 D.3
10.某地区为了解学生课余时间的读书情况,随机抽取了名学生进行调查,根据调查得到的学生日均课余读书时间绘制成如图所示的频率分布直方图,已知抽取的样本中日均课余读书时间低于10分钟的有10人,则图中的,的值分别为( )
A.200,0.015 B.100,0.010 C.100,0.015 D.1000,0.010
11.某中学举行了一次“环保知识竞赛”活动,为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本量为n)进行统计,按照,,,,的分组作出如图所示的频率分布直方图,但不慎丢失了部分数据.已知得分在的有8人,在的有2人,由此推测频率分布直方图中的( )
A.0.04 B.0.03 C.0.02 D.0.01
12.根据气象学上的标准,连续天的日平均气温低于即为入冬.现有甲、乙、丙、丁四地连续天的日平均温度的记录数据(记录数据都是正整数):
①甲地:个数据的中位数为,众数为;
②乙地:个数据的平均数为,极差为;
③丙地:个数据的平均数为,中位数为;
④丁地:个数据的平均数为,方差小于.
则肯定进入冬季的地区是( )
A.甲地 B.乙地 C.丙地 D.丁地
13.甲、乙、丙三名射箭运动员在某次测试中各射箭20次,三人的测试成绩如下表:分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则有( )
甲的成绩
环数 7 8 9 10
频数 5 5 5 5
乙的成绩
环数 7 8 9 10
频数 6 4 4 6
丙的成绩
环数 7 8 9 10
频数 4 6 6 4
A. B. C. D.
14.如图是某地某月1日至15日的日平均温度变化的折线图,根据该折线图,下列结论正确的是( )
A.由折线图能预测16日温度要低于19℃
B.这15天日平均温度的极差为18℃
C.连续三天日平均温度的方差最大的是7日,8日,9日三天
D.由折线图能预测本月温度小于25℃的天数少于温度大于25℃的天数
15.抽样统计甲射击运动员10次的训练成绩分别为86,85,88,86,90,89,88,87,85,92,则这10次成绩的80%分位数为( )
A.88.5 B.89 C.91 D.89.5
二、填空题
16.若一组数据为82,81,79,78,95,88,92,84,则该组数据的75%分位数是___________.
17.下图是国家统计局发布的2020年2月至2021年2月全国居民消费价格涨跌幅折线图;则给出下列三个结论:①2020年11月居民消费价格低于2019年同期;②2020年3月至7月居民的消费价格持续增长;③2020年7月的消费价格低于2020年3月的消费价格.其中所有正确结论的序号是________.
说明:1.在统计学中,同比是指本期统计数据与上一年同期统计数据相比较,例如年2月与2020年2月相比较;环比是指本期统计数据与上期统计数据相比较,例如2020年4月与年3月相比较.
2.同比增长率=,环比增长率=.
18.下图是国家统计局发布的2020年2月至2021年2月全国居民消费价格涨跌幅折线图.
说明:(1)在统计学中,同比是指本期统计数据与上一年同期统计数据相比较,例如2021年2月与2020年2月相比较:环比是指本期统计数据与上期统计数据相比较,例如2020年4月与2020年3月相比较.
(2)同比增长率环比增长率.
给出下列四个结论:
①2020年11月居民消费价格低于2019年同期;
②2020年3月至7月居民的消费价格持续增长;
③2020年3月的消费价格低于2020年4月的消费价格;
④2020年7月的消费价格低于2020年3月的消费价格.
其中所正确结论的序号是____________.
三、解答题
19.有20种不同的零食,每100g可食部分包含的能量(单位:kJ)如下:
110 120 123 165 432 190 174 235 428 318
249 280 162 146 210 120 123 120 150 140
(1)以上述20个数据组成总体,求总体平均数与总体标准差
(2)设计恰当的随机抽样方法,从总体中抽取一个容量为7的样本.
(3)利用上面的抽样方法,再抽取容量为7的样本,这个样本的平均数和标准差与(2)中的结果一样吗?为什么?
(4)利用(2)中的随机抽样方法,分别从总体中抽取一个容量为10,13,16,19的样本,分析样本容量与样本的平均数和标准差对总体的估计效果之间有什么关系.
20.在技术人员的指导下,某棉花种植基地的棉花产量和质量均有大幅度地提升,已知该棉花种植基地今年产量为,技术人员随机抽取了棉花,测量其马克隆值(棉花的马克隆值是反映棉花纤维细度与成熟度的综合指标,是棉纤维重要的内在质量指标之一,与棉花价格关系密切),得到如下统计表及不完整的频率分布直方图.
马克隆值
质量/ t 0.04 0.06 0.12 0.16 b a 0.06 0.03 0.01
(1)求表中的值,并补全频率分布直方图;
(2)根据频率分布直方图,估计样本的马克隆值的众数及中位数;
(3)根据马克隆值可将棉花分为三个等级,不同等级的棉花价格如下表所示:
马克隆值 或
级别
价格(万元/t) 1.6 1.52 1.44
用样本估计总体,估计该棉花种植基地今年的总产值.
21.为研究某植物园中某类植物的高度,随机抽取了高度在(单位:)的50株植物,得到其高度的频率分布直方图(如图所示).
(1)求的值;
(2)若园内有该植物1000株,试根据直方图信息估计高度在的植物数量.
22.某地区拟举办汉字听写大赛,某校为了选拔优秀的学生参加比赛,在本校举行了次汉字听写大赛,其中甲、乙两位同学的成绩最优异,由甲、乙两位同学的成绩绘制的茎叶图如图所示.已知甲成绩的中位数小于乙成绩的中位数.
(1)求的值;
(2)若要从甲、乙中选择一名同学参加该地区举办的汉字听写大赛,试从统计学的角度分析,选哪位同学比较合适.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
根据题意和表格的数据分别计算数据开发、数据分析、数据产品的平均薪资,进而比较大小即可.
【详解】
由题中选项知数据挖掘的平均薪资最高,故只需计算并比较其他三类工作岗位的平均薪资.估计数据开发的平均薪资为;
估计数据分析的平均薪资为;
估计数据产品的平均薪资为.
故数据挖掘>数据产品>数据开发>数据分析.
故选:B.
2.A
由题设条件,利用平均数和方差的计算公式计算即可求解.
【详解】
设7个数为,
则,
,
所以,
所以,
则这个数的平均数为,
方差为.
故选:A.
3.C
计算均值,再根据数据的集中度判断.
【详解】
甲的均值为,
乙的均值为,
两者均值相同,甲的方差为
乙的方差为
,
甲的方差小于乙的方差,甲稳定.
故选:C.
4.D
利用平均数、中位数、方差的定义直接求解.
【详解】
甲、乙、丙、丁、戊五位同学高一入学时年龄的平均数、中位数均为16,方差位0.8,
三年后,
这五位同学年龄的平均数变为16+3=19,故A正确;
这五位同学年龄的中位数变为16+3=19,故B正确;
这五位同学的方差不变,仍为0.8,故C正确,D错误.
故选:D.
5.B
根据频率分布直方图读出众数a,计算中位数b,平均数c,再比较大小.
【详解】
由频率分布直方图可知:众数;
中位数应落在70-80区间内,则有:,解得:;
平均数
=4.5+8.25+9.75+22.5+21.25+4.75=71
所以
故选:B
从频率分布直方图可以估计出的几个数据:
(1)众数:频率分布直方图中最高矩形的底边中点的横坐标;
(2)平均数:频率分布直方图每组数值的中间值乘以频率后相加;
(3)中位数:把频率分布直方图分成两个面积相等部分的平行于y轴的直线横坐标.
6.D
用频率分布直方图的相关知识和公式逐一计算验证选项.
【详解】
由频率分布直方图可得,成绩在的频率最高,因此考生人数最多,故A正确;
由频率分布直方图可得,成绩在的频率为,因此,不及格的人数为,故B正确;
由频率分布直方图可得:平均分等于,故C正确;
因为成绩在的频率为,由的频率为,所以中位数为,故D错误.
故选D.
本题考查频率分布直方图的众数、中位数、平均数以及样本容量的求法,考查学生的计算能力,熟记公式是解题的关键,属于中档题.
7.C
根据频率分布直方图,计算出频率为0.5时落在的组,0.5减去前几组的频率的差,再根据小长方形的面积可得出答案.
【详解】
由频率分布直方图得,第一组、第二组的频率为,
第三组的频率为,所以中位数落在第三组并设为,
则有,解得.
故选:C.
8.D
A.增长速度都是正值,工业增加值都在增加
B.可看到,最高点是在四月
C. 2020年10月工业增加值同比增长
【详解】
由题意可知该折线统计图是工业增加值同比增长率,2020年3月份到10月份,工业增加值同比都在增加,故A错误;
2020年3月份到10月份,工业增加值同比增加速度最大的是4月,增速为,故B错误;
2020年10月工业增加值同比增长,故C错误,D正确.
故选:D
9.D
根据直方图求出,求出的频率,可判断①;求出的频率,可判断②;根据中位数是从左到右频率为的分界点,先确定在哪个区间,再求出占该区间的比例,求出中位数,判断③.
【详解】
由,,
的频率为,①正确;
的频率为,②正确;
的频率为,的频率为,
中位数在且占该组的,
故中位数为,③正确.
故选:D.
本题考查补全直方图,由直方图求频率和平均数,属于基础题
10.B
根据频率分布直方图,由频率之和为1,列出方程即可求出;根据日均课余读书时间低于10分钟的人数,及其对应的频率,即可求出.
【详解】
利用频率之和为1可得,,解得,
根据频率、频数、样本容量之间关系可得,,解得.
故选:B.
11.B
根据频率分布直方图,先求得抽取学生的人数.
【详解】
得分在的有8人, 得分在的频率为
所以抽取中的人数为人
在的有2人,所以在的频率为,所以
∴由频率分布直方图各小矩形面积和为1,得.
解得.
故选:B.
本题考查了频率分布直方图的意义,补全频率分布直方图,属于基础题.
12.D
根据各地连续天的日平均温度的记录数据,通过特殊值法,可排除ABC选项;根据方差的计算公式,结合丁地的气温数据,可判断D正确.
【详解】
①甲地:个数据的中位数为,众数为;则这个数据可能为,,,,;即连续天的日平均气温不是都低于,所以甲地不一定入冬,故A错;
②乙地:个数据的平均数为,极差为;则这个数据可能为,,,,;即连续天的日平均气温不是都低于,所以乙地不一定入冬,故B错;
③丙地:个数据的平均数为,中位数为;则这个数据可能为,,,,;即连续天的日平均气温不是都低于,所以丙地不一定入冬,故C错;
④丁地:个数据的平均数为,方差小于.如有数据大于等于,则方差必大于等于,不满足题意,因此丁地这续天的日平均气温都低于,所以丁地一定入冬,故D正确;
故选:D.
13.B
分别根据平均数和方差公式,计算结果.
【详解】
,
,
,
,
,
,
由,得.
故选:B
结论点睛:本题考查平均数和方差的计算,
1.平均数
2.方差,
3.标准差,
4.平均数大说明样本的平均水平高,方差和标准差大说明样本比较分散,与平均水平差距较大,不稳定.
14.C
根据图象中的信息,逐个选项分析处理即可.
【详解】
A选项,由折线图无法预测16日温度要是否低于19℃,故A错误;
B选项,这15天日平均温度的极差为19℃,B错误;
C选项,日平均温度的方差的大小取决于日平均温度的波动的大小,7,8,9三日的日平均温度的波动最大,故日平均温度的方差最大,C正确;
D选项,由折线图无法预测本月温度小于19℃的天数是否少于温度大于25℃的天数,故D错误.
故选:C.
15.D
将数据从小到大排列,计算,得到答案.
【详解】
甲射击运动员10次的训练成绩从小到大分别为:85,85,86,86,87,88,88,89,90,92.
,这10次成绩的80%分位数为:.
故选:D.
16.90
可得该组数据的75%分位数在第6位和第7位之间,求出平均值即可.
【详解】
由题可得一共有8个数据,则该组数据的75%分位数在第6位和第7位之间,为.
故答案为:90.
17.①③
根据题中数据,根据环比、同比增长率的概念,即可判断①②的正误;设2020年3月居民消费价格为,4月消费价格为,5月消费价格为,6月消费价格为,7月消费价格为,根据环比增长率的公式,即可求得与的关系,同理可求得与的关系,即可判断③的正误,即可得答案.
【详解】
对于①:由图可知2020年11月同比增长率为-0.5,由同比增长率的计算公式可得,2020年11月居民消费价格低于2019年同期,故①正确;
对于②:由图可知,2020年3月至6月的环比增长率为负,由环比增长率的计算公式可得消费价格下降,故②错误;
对于③:设2020年3月居民消费价格为,4月消费价格为,5月消费价格为,6月消费价格为,7月消费价格为,
由题意得:,解得,
,解得,
,解得,
,解得,
所以,
所以2020年7月消费价格低于2020年3月消费价格,故③正确.
故答案为:①③
18.①④
根据国居民消费价格涨跌幅折线图,结合题中说明和计算公式逐一判断即可.
【详解】
①:由国居民消费价格涨跌幅折线图可知:同比增长率为,由题中说明所给同比增长率定义可知:2020年11月居民消费价格低于2019年同期,故本结论正确;
②:由国居民消费价格涨跌幅折线图可知:2020年3月至6月环比增长率为负值,由题中所给的环比增长率定义可知:2020年3月至6月居民的消费价格持续下降,所以本结论不正确;
③:设2020年3月的消费价格为,2020年4月的消费价格为,
根据题中所给的环比增长率公式可得:,
所以,因此本结论不正确;
④:设2020年5月的消费价格为,2020年6月的消费价格为,2020年7月的消费价格为,
根据题中所给的环比增长率公式可得:
,,
,所以,因此本结论正确;
故答案为:①④
关键点睛:理解同比增长率、环比增长率的定义,运用同比增长率、环比增长率的公式进行解题是关键.
19.(1)平均数为199.75,总体标准差为95.26;(2)抓阄法;(3)(2)和(3)的计算结果不相同的概率相当大,而相同的概率很小;(4)由于样本的随机性,也有极个别(小概率)的例外情况.
(1)由平均数和方差公式计算;
(2)用抓阄法进行抽样;
(3)由于抽样的随机性,两种结果相同的概率很小,不同概率很大.
(4)由于样本容量增大,估计总体的精确程度会提高,效果更好(也有个别现象效果不好).
【详解】
(1)总体平均数为199.75.
总体标准差为95.26.
(2)可以使用抓阄法进行抽样.
(3)由样本的随机性,知(2)和(3)的计算结果不相同的概率相当大,而相同的概率很小.
(4)随着样本容量的增加,分别用样本平均数和样本标准差估计总体平均数和总体标准差的效果会越来越好(即精度会越来越高).但是由于样本的随机性,也有极个别(小概率)的例外情况.
本题考查用样本估计总体,样本容量越大时,估计效果可能会更好些.
20.(1),,频率分布直方图见解析;
(2)众数为,中位数为;
(3)万元.
(1)由频率分布直方图和统计表可计算求得,由此可补全频率分布直方图;
(2)由频率分布直方图估计众数和中位数的方法直接求解即可;
(3)计算求得样本的产值,进而可得今年的总产值.
(1)
由题中频率分布直方图知:;
由统计表得:,
解得:.
补全的频率分布直方图如图所示:
(2)
由频率分布直方图知:马克隆值落在区间内的频率最大,故众数为.
,,中位数在区间内,
中位数为.
(3)
样本的产值为(万元),
估计该棉花种植基地今年的总产值为(万元).
21.(1);(2)280.
频率分布直方图中矩形面积和为1可得的值;
算出高度落在的植物的频率可得.
【详解】
(1),
解得;
(2)高度落在的植物的频率为,
高度在的植物数量为株
此题为统计基础题,考查频率分布直方图的含义.
22.(1)0;(2)乙同学比较合适.
(1)由乙的中位数为91,甲的中位数(90+x)小于91得解;
(2)计算甲乙二人三次成绩的平均数、方差等特征数据,再分析选择.
【详解】
(1)由茎叶图可知,乙同学成绩的中位数为.
又由茎叶图可得甲同学成绩的中位数大于或等于,
且甲成绩的中位数小于乙成绩的中位数,所以甲同学成绩的中位数只能为,
故.
(2)甲同学成绩的平均数为,
乙同学成绩的平均数为,
所以甲、乙成绩的平均数相等.
甲同学成绩的方差,
乙同学成绩的方差,
,所以乙同学的成绩更稳定,选乙同学比较合适.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
