2021-2022学年下学期上海初中数学七年级期末典型试卷2(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年下学期上海初中数学七年级期末典型试卷2(Word版,附答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 185.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-14 23:53:35 | ||
图片预览




文档简介
2021-2022学年下学期上海初中数学七年级期末典型试卷2
一.选择题(共6小题,满分18分,每小题3分)
1.(3分)(2021秋 韶关期末)已知三角形的两边长分别为4和9,则下列数据中,能作为第三边长的是( )
A.2 B.3 C.4 D.9
2.(3分)(2021春 温江区校级期中)下列运算正确的是( )
A.(2m﹣3)(﹣2m+3)=﹣4m2﹣9 B.(2m+1)(2m﹣1)=2m2﹣1
C.(﹣2m﹣1)2=4m2+4m+1 D.(2m+3)2=4m2+6m+9
3.(3分)下列各数中,最小的是( )
A. B. C. D.
4.(3分)下列说法正确的是( )
A.有两边及一边的对角分别相等的两个三角形全等
B.有两边相等的两个直角三角形全等
C.有两个角及第三个角的对边分别相等的两个三角形全等
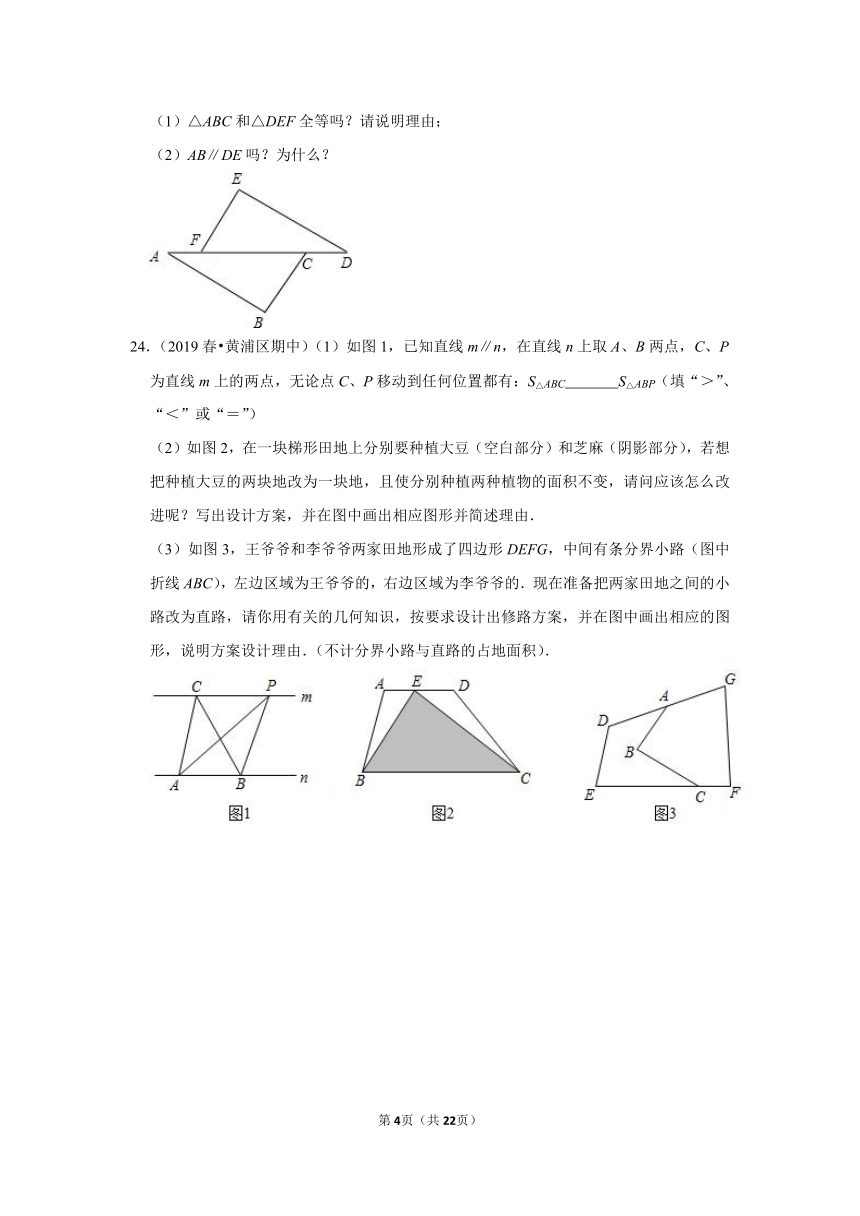
D.有两个角及一边相等的两个三角形全等
5.(3分)(2021春 静安区校级期末)如图,直线a、b被直线c所截,下列说法正确的是( )
A.当a∥b时,一定有∠1=∠2
B.当∠1=∠2时,一定有a∥b
C.当a∥b时,一定有∠1+∠2=90°
D.当∠1+∠2=180°时,一定有a∥b
6.(3分)(2021秋 射洪市期中)已知,则的算术平方根是( )
A. B. C.±2 D.2
二.填空题(共11小题,满分18分)
7.(3分)(2021春 普陀区期中)2021年1月份国家统计局发布数据显示,初步核算,2020年全年国内生产总值(GDP)为1015986亿元.请将数字“1015986”保留3个有效数字并用科学记数法表示为 .
8.(3分)(2020 雁塔区校级模拟)已知实数(3)0,,,0.101001,,,其中为无理数的是 .
9.(3分)(2021春 静安区校级期末)在数轴上,点A、点B对应的数分别是和,则AB= .
10.(3分)(2021 西城区校级开学)6 .
11.(2021春 闵行区校级期中)比较大小: .
12.(3分)(2020秋 铜官区期末)已知:2x+3y+3=0,计算:4x 8y的值= .
13.(2021春 嘉定区期末)在△ABC中,如果∠A:∠B:∠C=3:4:5,那么∠A= .
14.(2021春 嘉定区期末)如果将点M(m,3)向左平移2个单位到达点N,这时点N恰好在y轴上,那么m的值是 .
15.(2021春 嘉定区期末)如图,AD∥CE,△ACD的面积为a,那么△EAD的面积为 .
16.(2019春 连云港期末)如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.如图2,若∠MPN=75°,且射线PQ绕点P从PN位置开始,以每秒15°的速度逆时针旋转,射线PM同时绕点P以每秒5°的速度逆时针旋转,当PQ与PN成180°时,PQ与PM同时停止旋转,设旋转的时间为t秒.当射线PQ是∠MPN的“巧分线”时,t的值为 .
17.(3分)(2019春 丰城市期末)将一副三角板按如图放置,小明得到下列结论:①如果∠2=30°,则有AC∥DE;②∠BAE+∠CAD=180°;③如果BC∥AD,则有∠2=30°;④如果∠CAD=150°,则∠4=∠C;那么其中正确的结论有 .
三.解答题(共7小题,满分46分)
18.(2021春 嘉定区期末)计算:(2)2﹣(1).
19.(12分)(2018春 静安区期中)()0+(28)﹣()﹣2
20.(10分)(2021春 静安区校级期末)已知BC=4,根据下列条件,画图及填空:
(1)画△ABC,使∠B=30°,∠C=60°.
(2)在(1)的条件下,画△ABC的中线BD.
(3)在(1)、(2)的条件下,从∠A引出一条射线,将△ABC切割成两个等腰三角形,射线与边BC相交于点E,请画出射线AE,在图中标出∠CAE的大小,并写出CD= .
21.(8分)(2021春 虹口区校级期末)∠1与∠2互补,∠2比∠1的3倍的大20°,求∠1、∠2的大小.
22.(8分)(2020春 覃塘区期末)如图,D,E,G分别是AB,AC,BC边上的点,∠1+∠2=180°,∠3=∠B.
(1)请说明DE∥BC的理由;
(2)若DE平分∠ADC,∠2=2∠B,判断CD与EG的位置关系,并说明理由.
23.(8分)(2010春 吉安期末)如图,在△ABC和△DEF中,∠B=∠E=90°,BC=a,AC=b,EF=m,DF=n,且a、b、m、n满足下列条件:(a﹣m)2+|b﹣n|=0.
(1)△ABC和△DEF全等吗?请说明理由;
(2)AB∥DE吗?为什么?
24.(2019春 黄浦区期中)(1)如图1,已知直线m∥n,在直线n上取A、B两点,C、P为直线m上的两点,无论点C、P移动到任何位置都有:S△ABC S△ABP(填“>”、“<”或“=”)
(2)如图2,在一块梯形田地上分别要种植大豆(空白部分)和芝麻(阴影部分),若想把种植大豆的两块地改为一块地,且使分别种植两种植物的面积不变,请问应该怎么改进呢?写出设计方案,并在图中画出相应图形并简述理由.
(3)如图3,王爷爷和李爷爷两家田地形成了四边形DEFG,中间有条分界小路(图中折线ABC),左边区域为王爷爷的,右边区域为李爷爷的.现在准备把两家田地之间的小路改为直路,请你用有关的几何知识,按要求设计出修路方案,并在图中画出相应的图形,说明方案设计理由.(不计分界小路与直路的占地面积).
2021-2022学年下学期上海初中数学七年级期末典型试卷2
参考答案与试题解析
一.选择题(共6小题,满分18分,每小题3分)
1.(3分)(2021秋 韶关期末)已知三角形的两边长分别为4和9,则下列数据中,能作为第三边长的是( )
A.2 B.3 C.4 D.9
【考点】三角形三边关系.
【专题】三角形;推理能力.
【分析】首先根据三角形的三边关系定理,求得第三边的取值范围,再进一步找到符合条件的数值.
【解答】解:设这个三角形的第三边为x.
根据三角形的三边关系定理,得:9﹣4<x<9+4,
解得5<x<13.
故选:D.
【点评】本题考查了三角形的三边关系定理.掌握构成三角形的条件:两边之和>第三边,两边之差<第三边是解决问题的关键.
2.(3分)(2021春 温江区校级期中)下列运算正确的是( )
A.(2m﹣3)(﹣2m+3)=﹣4m2﹣9 B.(2m+1)(2m﹣1)=2m2﹣1
C.(﹣2m﹣1)2=4m2+4m+1 D.(2m+3)2=4m2+6m+9
【考点】平方差公式;完全平方公式.
【专题】整式;运算能力.
【分析】根据平方差公式、完全平方公式结构特征进行判断即可.
【解答】解:A.(2m﹣3)(﹣2m+3)=﹣4m2+12m﹣9,因此选项A不符合题意;
B.(2m+1)(2m﹣1)=4m2﹣1,因此选项B不符合题意;
C.(﹣2m﹣1)2=4m2+4m+1,因此选项C符合题意;
D.(2m+3)2=4m2+12m+9,因此选项D不符合题意;
故选:C.
【点评】本题考查平方差公式、完全平方公式,掌握完全平方公式、平方差公式的结构特征是正确解答的前提.
3.(3分)下列各数中,最小的是( )
A. B. C. D.
【考点】分数指数幂;实数大小比较.
【专题】计算题.
【分析】根据分数指数幂的运算即可求出答案.
【解答】解:(A)()6=23=8,
(B)原式=()6=32=9,
(C)原式=()623=8,
(D)原式=()6=6,
故选:D.
【点评】本题考查分数指数幂,解题的关键是熟练运用分数指数幂的运算,本题属于基础题型.
4.(3分)下列说法正确的是( )
A.有两边及一边的对角分别相等的两个三角形全等
B.有两边相等的两个直角三角形全等
C.有两个角及第三个角的对边分别相等的两个三角形全等
D.有两个角及一边相等的两个三角形全等
【考点】直角三角形全等的判定;等腰三角形的性质;勾股定理;全等三角形的判定.
【专题】图形的全等;推理能力.
【分析】根据全等三角形的判定判断即可.
【解答】解:A、有两边及一边的对角分别相等的两个三角形不一定全等,说法错误,不符合题意;
B、有两边相等的两个直角三角形不一定全等,说法错误,不符合题意;
C、有两个角及第三个角的对边分别相等的两个三角形全等,说法正确,符合题意;
D、有两个角及一边相等的两个三角形不一定全等,说法错误,不符合题意;
故选:C.
【点评】本题考查了全等三角形的判定定理的理解,能熟练地运用判定定理进行推理是解此题的关键.
5.(3分)(2021春 静安区校级期末)如图,直线a、b被直线c所截,下列说法正确的是( )
A.当a∥b时,一定有∠1=∠2
B.当∠1=∠2时,一定有a∥b
C.当a∥b时,一定有∠1+∠2=90°
D.当∠1+∠2=180°时,一定有a∥b
【考点】平行线的判定与性质.
【专题】线段、角、相交线与平行线;推理能力.
【分析】根据平行线的判定定理即性质定理求解判断即可.
【解答】解:如图,
A、当a∥b时,∠1=∠3,
∵∠2+∠3=180°,
∴∠2+∠1=180°,
故A错误,不符合题意;
B、当∠1=∠2时,且∠1=∠2=90°,才有a∥b,
故B错误,不符合题意;
C、当a∥b时,∠1=∠3,
∵∠3+∠2=180°,
∴∠1+∠2=180°,
故C错误,不符合题意;
D、当∠1+∠2=180°时,
∵∠3+∠2=180°,
∴∠1=∠3,
∴一定有a∥b,
故D正确,符合题意;
故选:D.
【点评】此题考查了平行线的判定与性质,熟练掌握平行线的判定定理与性质定理是解题的关键.
6.(3分)(2021秋 射洪市期中)已知,则的算术平方根是( )
A. B. C.±2 D.2
【考点】二次根式有意义的条件.
【专题】二次根式;运算能力.
【分析】根据二次根式有意义的条件求出b,进而求出a,根据算术平方根的概念计算即可.
【解答】解:由题意得:b﹣8≥0,8﹣b≥0,
解得:b=8,
则a=2,
∴4,
∵4的算术平方根是2,
∴的算术平方根是2,
故选:D.
【点评】本题考查的是二次根式有意义的条件,算术平方根,掌握二次根式的被开方数是非负数是解题的关键.
二.填空题(共11小题,满分18分)
7.(3分)(2021春 普陀区期中)2021年1月份国家统计局发布数据显示,初步核算,2020年全年国内生产总值(GDP)为1015986亿元.请将数字“1015986”保留3个有效数字并用科学记数法表示为 1.02×106 .
【考点】科学记数法与有效数字.
【专题】计算题;实数;运算能力.
【分析】用科学记数法保留有效数字,要在标准形式a×10n中a的部分保留,从左边第一个不为0的数字数起,需要保留几位就数几位,然后根据四舍五入的原理进行取舍.
【解答】解:1015986=1.015986×106≈1.02×106.
故答案是:1.02×106.
【点评】本题主要考查了科学记数法以及有效数字,从左边第一个不是0的数开始数起,到精确到的数位为止,所有的数字都叫做这个数的有效数字;注意后面的单位不算入有效数字.
8.(3分)(2020 雁塔区校级模拟)已知实数(3)0,,,0.101001,,,其中为无理数的是 , .
【考点】无理数;零指数幂;算术平方根;立方根.
【专题】实数;数感.
【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此进行解答即可.
【解答】解:(3)0=1,是整数,属于有理数;
0.101001是有限小数,属于有理数;
是分数,属于有理数;
,是整数,属于有理数;
无理数有:,.
故答案为:,.
【点评】此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.
9.(3分)(2021春 静安区校级期末)在数轴上,点A、点B对应的数分别是和,则AB= 3 .
【考点】实数与数轴.
【分析】本题依据绝对值的实际意义,任意两点间的距离等于这两个点所代表的数差的绝对值即得到答案.
【解答】解:∵点A、点B对应的数分别是和,∴.
故答案为:.
【点评】本题主要考查了数轴上两点之间距离的求法,关键需要灵活应用绝对值得实际意义.
10.(3分)(2021 西城区校级开学)6 3 .
【考点】二次根式的混合运算.
【专题】二次根式;运算能力.
【分析】直接化简二次根式,再利用二次根式的乘法运算法则化简,进而合并同类二次根式得出答案.
【解答】解:原式6
=22
=3.
故答案为:3.
【点评】此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.
11.(2021春 闵行区校级期中)比较大小: > .
【考点】实数大小比较.
【分析】分别计算出()2和()2的值,比较和的大小,变形即可得到答案.
【解答】解:∵()2=28+2,
()2=28+2,
∴),
∴.
故答案为:>.
【点评】本题考查的是实数的大小比较,掌握完全平方公式、正确进行不等式的变形是解题的关键.
12.(3分)(2020秋 铜官区期末)已知:2x+3y+3=0,计算:4x 8y的值= .
【考点】幂的乘方与积的乘方;同底数幂的乘法.
【专题】计算题;整式;数感;运算能力.
【分析】根据幂的乘方与积的乘方、同底数幂的乘法的计算公式即可得结果.
【解答】解:∵2x+3y+3=0,
∴2x+3y=﹣3,
4x 8y=22x 23y=2(2x+3y)=2﹣3.
故答案为:.
【点评】本题考查了幂的乘方与积的乘方、同底数幂的乘法,解决本题的关键是掌握幂的乘方与积的乘方、同底数幂的乘法.
13.(2021春 嘉定区期末)在△ABC中,如果∠A:∠B:∠C=3:4:5,那么∠A= 45° .
【考点】三角形内角和定理.
【专题】三角形;推理能力.
【分析】根据三个角的比可设设∠A=3x,∠B=4x,∠C=5x,再利用三角形的内角和定理列方程,解方程可求解x值,即可求解∠A的度数.
【解答】解:设∠A=3x,∠B=4x,∠C=5x,
∵∠A+∠B+∠C=180°,
∴3x+4x+5x=180°,
解得x=15°,
∴∠A=3x=45°,
故答案为:45°.
【点评】本题主要考查三角形的内角和定理,运用方程思想解决问题是解题的关键.
14.(2021春 嘉定区期末)如果将点M(m,3)向左平移2个单位到达点N,这时点N恰好在y轴上,那么m的值是 2 .
【考点】坐标与图形变化﹣平移.
【专题】平面直角坐标系;平移、旋转与对称;符号意识.
【分析】根据向右平移横坐标加,向上平移纵坐标加即可得解.
【解答】解:将点M(m,3)向左平移2个单位到达点N,这时点N恰好在y轴上,
∴m﹣2=0,
∴m=2.
故答案为:2.
【点评】本题考查了坐标与图形变化﹣平移,熟记平移中点的变化规律:横坐标右移加,左移减;纵坐标上移加,下移减是解题的关键.
15.(2021春 嘉定区期末)如图,AD∥CE,△ACD的面积为a,那么△EAD的面积为 a .
【考点】三角形的面积;平行线之间的距离.
【专题】三角形;推理能力.
【分析】利用平行线之间的距离处处相等得到C点和E点到AD的距离相等,然后利用三角形面积公式求解.
【解答】解:∵AD∥CE,
∴C点和E点到AD的距离相等,
∴S△EAD=S△CAD=a.
故答案为:a.
【点评】本题考查了三角形的面积:三角形的面积等于底边长与高线乘积的一半,即S△底×高.也考查了平行线之间的距离.
16.(2019春 连云港期末)如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.如图2,若∠MPN=75°,且射线PQ绕点P从PN位置开始,以每秒15°的速度逆时针旋转,射线PM同时绕点P以每秒5°的速度逆时针旋转,当PQ与PN成180°时,PQ与PM同时停止旋转,设旋转的时间为t秒.当射线PQ是∠MPN的“巧分线”时,t的值为 3或或 .
【考点】角的计算.
【专题】分类讨论;线段、角、相交线与平行线.
【分析】分3种情况,根据巧分线定义得到方程求解即可.
【解答】解:当∠NPQ∠MPN时,
15t(75+5t),
解得t=3;
当∠NPQ∠MPN时,
15t(75+5t),
解得t.
当∠NPQ∠MPN时,
15t(75+5t),
解得t.
故t的值为3或或.
故答案为:3或或.
【点评】本题考查了旋转的性质,巧分线定义,学生的阅读理解能力及知识的迁移能力.理解“巧分线”的定义是解题的关键.
17.(3分)(2019春 丰城市期末)将一副三角板按如图放置,小明得到下列结论:①如果∠2=30°,则有AC∥DE;②∠BAE+∠CAD=180°;③如果BC∥AD,则有∠2=30°;④如果∠CAD=150°,则∠4=∠C;那么其中正确的结论有 ①②④ .
【考点】平行线的判定与性质.
【专题】线段、角、相交线与平行线;三角形.
【分析】根据平行线的性质和判定和三角形内角和定理逐个判断即可.
【解答】解:∵∠2=30°,∠CAB=90°,
∴∠1=60°,
∵∠E=60°,
∴∠1=∠E,
∴AC∥DE,故①正确;
∵∠CAB=∠DAE=90°,
∴∠BAE+∠CAD=90°﹣∠1+90°+∠1=180°,故②正确;
∵BC∥AD,∠B=45°,
∴∠3=∠B=45°,
∵∠2+∠3=∠DAE=90°,
∴∠2=45°,故③错误;
∵∠CAD=150°,∠BAE+∠CAD=180°,
∴∠BAE=30°,
∵∠E=60°,
∴∠BOE=∠BAE+∠E=90°,
∴∠4+∠B=90°,
∵∠B=45°,
∴∠4=45°,
∵∠C=45°,
∴∠4=∠C,故④正确;
故答案为:①②④.
【点评】本题考查了三角形的内角和定理和平行线的性质和判定,能灵活运用定理进行推理是解此题的关键.
三.解答题(共7小题,满分46分)
18.(2021春 嘉定区期末)计算:(2)2﹣(1).
【考点】二次根式的混合运算.
【专题】二次根式;运算能力.
【分析】先利用完全平方公式、二次根式的乘法法则和二次根式的性质计算,然后合并即可.
【解答】解:原式=3﹣44﹣3
=3﹣44﹣34
=﹣3.
【点评】本题考查了二次根式的混合运算:熟练掌握二次根式的性质、二次根式的乘法法则是解决问题的关键.
19.(12分)(2018春 静安区期中)()0+(28)﹣()﹣2
【考点】实数的运算;分数指数幂;零指数幂;负整数指数幂.
【专题】计算题.
【分析】首先计算乘方、乘法,然后从左向右依次计算,求出算式的值是多少即可.
【解答】解:()0+(28)﹣()﹣2
=1+4﹣9
=﹣4
【点评】此题主要考查了实数的运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.
20.(10分)(2021春 静安区校级期末)已知BC=4,根据下列条件,画图及填空:
(1)画△ABC,使∠B=30°,∠C=60°.
(2)在(1)的条件下,画△ABC的中线BD.
(3)在(1)、(2)的条件下,从∠A引出一条射线,将△ABC切割成两个等腰三角形,射线与边BC相交于点E,请画出射线AE,在图中标出∠CAE的大小,并写出CD= 1 .
【考点】作图—复杂作图;线段垂直平分线的性质;等腰三角形的性质.
【专题】作图题;几何直观;应用意识.
【分析】(1)如图1所示,将量角器中心与点B对齐,0刻度线与BC对齐,内圈30°线条指向作射线BP;将量角器中心与点C对齐,0刻度线与BC对齐,外圈60°线条指向作射线CQ;射线BP与CQ交点为点A,则△ABC即为所求.
(2)如图2所示,取AC中点为点D,作线段BD,则BD为△ABC的中线,线段BD即为所求.
(3)在△ABC内部作∠CAE=∠C=60°,射线AE即为所求.
【解答】解:(1)如图1中,△ABC即为所求;
(2)如图2中,线段BD即为所求;
(3)如图3所示,射线AE即为所求.
∵∠ABC=30°,∠C=60°,
∴∠BAC=90°,
∴ACBC=2,
∴CD=AD=1,
故答案为:1.
【点评】本题考查作图﹣复杂作图,等腰三角形的性质,直角三角形30度角的性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
21.(8分)(2021春 虹口区校级期末)∠1与∠2互补,∠2比∠1的3倍的大20°,求∠1、∠2的大小.
【考点】余角和补角.
【专题】线段、角、相交线与平行线;推理能力.
【分析】直接利用补角的定义结合∠2比∠1的3倍的大20°,得出等式求出答案.
【解答】解:由题意得,
则有∠1+3∠1+20°=180°,4∠1=160°,∠1=40°,
则∠2=3∠1+20°=3×40°+20°=140°,
∴∠1=40°;∠2=140°.
【点评】本题考查了余角和补角,掌握余角和补角的性质是解题的关键.
22.(8分)(2020春 覃塘区期末)如图,D,E,G分别是AB,AC,BC边上的点,∠1+∠2=180°,∠3=∠B.
(1)请说明DE∥BC的理由;
(2)若DE平分∠ADC,∠2=2∠B,判断CD与EG的位置关系,并说明理由.
【考点】平行线的判定与性质.
【专题】线段、角、相交线与平行线;推理能力.
【分析】(1)根据已知条件和对顶角相等可证明AB∥EG,再根据平行线的性质得角相等,再等量代换可得∠3=∠EGC,进而可得DE∥BC;
(2)根据已知条件可得∠B=45°,可以证明CD⊥AB,再由AB∥EG,即可得CD⊥EG.
【解答】解:(1)∵∠1+∠2=180°,∠1=∠DFG,
∴∠1+∠DFG=180°,
∴AB∥EG,
∴∠B=∠EGC,
又∵∠B=∠3,
∴∠3=∠EGC,
∴DE∥BC;
(2)CD⊥EG.
理由如下:
∵DE平分∠ADC,
∴∠ADE=∠EDC,
∵DE∥BC,
∴∠B=∠ADE=∠EDC,
又∵∠2=2∠B,∠2+∠ADE+∠EDC=180°,
∴2∠B+∠B+∠B=180°,
∴∠B=45°,
∴∠2=2∠B=90°,
∴CD⊥AB
又∵AB∥EG,
∴CD⊥EG.
【点评】本题考查了平行线的判定与性质,解决本题的关键是区别平行线的判定与性质并熟练运用.
23.(8分)(2010春 吉安期末)如图,在△ABC和△DEF中,∠B=∠E=90°,BC=a,AC=b,EF=m,DF=n,且a、b、m、n满足下列条件:(a﹣m)2+|b﹣n|=0.
(1)△ABC和△DEF全等吗?请说明理由;
(2)AB∥DE吗?为什么?
【考点】全等三角形的判定与性质;非负数的性质:绝对值;非负数的性质:偶次方;平行线的判定.
【专题】证明题;探究型.
【分析】(1)首先解等式根据非负数性质,可判断a=m,b=n;则BC=EF,AC=DF;由∠B=∠E=90°,易得△ABC≌△DEF.
(2)利用第(1)问的全等可得到∠A=∠D,所以AB∥DE(内错角相等,两直线平行).
【解答】解:(1)△ABC≌△DEF;
理由:(a﹣m)2+|b﹣n|=0,
∵(a﹣m)2≥0,|b﹣n|≥0,
∴a﹣m=0,b﹣n=0,a=m,b=n;
∵BC=a,AC=b,EF=m,DF=n,
∴BC=EF,AC=DF;
在Rt△ABC和Rt△DEF中,
AC=DF,BC=EF,
∴Rt△ABC≌Rt△DEF(HL);
(2)AB∥DE;
理由:∵△ABC≌△DEF(已证),
∴∠A=∠D(全等三角形对应角相等),
∴AB∥DE(内错角相等,两直线平行).
【点评】本题考查了全等三角形的判定和性质;题目通过解等式考查了非负数的性质,而且得到了线段之间相等的关系,从而能判三角形全等;由三角形全等得到角相等,又确定了两直线的平行关系;考法新颖,是一道考查学生综合能力的好题.
24.(2019春 黄浦区期中)(1)如图1,已知直线m∥n,在直线n上取A、B两点,C、P为直线m上的两点,无论点C、P移动到任何位置都有:S△ABC = S△ABP(填“>”、“<”或“=”)
(2)如图2,在一块梯形田地上分别要种植大豆(空白部分)和芝麻(阴影部分),若想把种植大豆的两块地改为一块地,且使分别种植两种植物的面积不变,请问应该怎么改进呢?写出设计方案,并在图中画出相应图形并简述理由.
(3)如图3,王爷爷和李爷爷两家田地形成了四边形DEFG,中间有条分界小路(图中折线ABC),左边区域为王爷爷的,右边区域为李爷爷的.现在准备把两家田地之间的小路改为直路,请你用有关的几何知识,按要求设计出修路方案,并在图中画出相应的图形,说明方案设计理由.(不计分界小路与直路的占地面积).
【考点】作图—应用与设计作图;平行线之间的距离;三角形的面积;梯形.
【专题】作图题;几何直观;运算能力;推理能力.
【分析】(1)根据等底等高的三角形面积相等即可得结论;
(2)根据同底等高的三角形面积相等即可设计改进方案;
(3)根据同底等高的三角形面积相等即可设计修路方案.
【解答】解:(1)∵m∥n,
∴△ABC与△ABP等底等高,
∴S△ABC=S△ABP.
故答案为:=;
(2)方法一:
连接AC,将△ACD的区域用于种植大豆,
△ABC的区域用于种植芝麻,
理由:由于同底等高,
所以S△ACE=S△ABE,
所以S△ABE+S△ECD=S△ACE+S△ECD,
即S△ACD=S△ABE+S△ECD,
同理S△ACB=S△BCE,
方法二
连接BD,将△ABD的区域用于种植大豆,
△BCD的区域用于种植芝麻,
理由:由于同底等高,
所以S△BED=S△ECD,
所以S△ABE+S△ECD=S△ABE+S△BED,
即S△ABD=S△ABE+S△ECD,
同理S△BCD=S△BCE.
(3)方法一
连接AC,过B点作AC的平行线PQ,
连接AQ,AQ即为所修直路.
将四边形ADEQ的区域分给王爷爷,
四边形AGFQ的区域分给李爷爷,
理由:由于同底等高,
所以S△BCQ=S△ABQ,
所以S△ABP+S△BCQ=S△ABP+S△ABQ,
即S△APQ=S△ABP+S△BCQ,
同理S△ABC=S△ACQ.
方法二:
连接AC,过B点作AC的平行线PQ,
连接PC,PC即为所修直路.
将四边形CEDP的区域分给王爷爷,
四边形CPGF的区域分给李爷爷,
理由:由于同底等高,
所以S△ABP=S△PBC,
所以S△ABP+S△BCQ=S△PBC+S△BCQ.
即S△CPQ=S△APB+S△BCQ.
同理S△ABC=S△ACP.
【点评】本题考查了作图﹣应用与设计作图,解决本题的关键是掌握等底等高的两个三角形的面积相等
第1页(共1页)
一.选择题(共6小题,满分18分,每小题3分)
1.(3分)(2021秋 韶关期末)已知三角形的两边长分别为4和9,则下列数据中,能作为第三边长的是( )
A.2 B.3 C.4 D.9
2.(3分)(2021春 温江区校级期中)下列运算正确的是( )
A.(2m﹣3)(﹣2m+3)=﹣4m2﹣9 B.(2m+1)(2m﹣1)=2m2﹣1
C.(﹣2m﹣1)2=4m2+4m+1 D.(2m+3)2=4m2+6m+9
3.(3分)下列各数中,最小的是( )
A. B. C. D.
4.(3分)下列说法正确的是( )
A.有两边及一边的对角分别相等的两个三角形全等
B.有两边相等的两个直角三角形全等
C.有两个角及第三个角的对边分别相等的两个三角形全等
D.有两个角及一边相等的两个三角形全等
5.(3分)(2021春 静安区校级期末)如图,直线a、b被直线c所截,下列说法正确的是( )
A.当a∥b时,一定有∠1=∠2
B.当∠1=∠2时,一定有a∥b
C.当a∥b时,一定有∠1+∠2=90°
D.当∠1+∠2=180°时,一定有a∥b
6.(3分)(2021秋 射洪市期中)已知,则的算术平方根是( )
A. B. C.±2 D.2
二.填空题(共11小题,满分18分)
7.(3分)(2021春 普陀区期中)2021年1月份国家统计局发布数据显示,初步核算,2020年全年国内生产总值(GDP)为1015986亿元.请将数字“1015986”保留3个有效数字并用科学记数法表示为 .
8.(3分)(2020 雁塔区校级模拟)已知实数(3)0,,,0.101001,,,其中为无理数的是 .
9.(3分)(2021春 静安区校级期末)在数轴上,点A、点B对应的数分别是和,则AB= .
10.(3分)(2021 西城区校级开学)6 .
11.(2021春 闵行区校级期中)比较大小: .
12.(3分)(2020秋 铜官区期末)已知:2x+3y+3=0,计算:4x 8y的值= .
13.(2021春 嘉定区期末)在△ABC中,如果∠A:∠B:∠C=3:4:5,那么∠A= .
14.(2021春 嘉定区期末)如果将点M(m,3)向左平移2个单位到达点N,这时点N恰好在y轴上,那么m的值是 .
15.(2021春 嘉定区期末)如图,AD∥CE,△ACD的面积为a,那么△EAD的面积为 .
16.(2019春 连云港期末)如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.如图2,若∠MPN=75°,且射线PQ绕点P从PN位置开始,以每秒15°的速度逆时针旋转,射线PM同时绕点P以每秒5°的速度逆时针旋转,当PQ与PN成180°时,PQ与PM同时停止旋转,设旋转的时间为t秒.当射线PQ是∠MPN的“巧分线”时,t的值为 .
17.(3分)(2019春 丰城市期末)将一副三角板按如图放置,小明得到下列结论:①如果∠2=30°,则有AC∥DE;②∠BAE+∠CAD=180°;③如果BC∥AD,则有∠2=30°;④如果∠CAD=150°,则∠4=∠C;那么其中正确的结论有 .
三.解答题(共7小题,满分46分)
18.(2021春 嘉定区期末)计算:(2)2﹣(1).
19.(12分)(2018春 静安区期中)()0+(28)﹣()﹣2
20.(10分)(2021春 静安区校级期末)已知BC=4,根据下列条件,画图及填空:
(1)画△ABC,使∠B=30°,∠C=60°.
(2)在(1)的条件下,画△ABC的中线BD.
(3)在(1)、(2)的条件下,从∠A引出一条射线,将△ABC切割成两个等腰三角形,射线与边BC相交于点E,请画出射线AE,在图中标出∠CAE的大小,并写出CD= .
21.(8分)(2021春 虹口区校级期末)∠1与∠2互补,∠2比∠1的3倍的大20°,求∠1、∠2的大小.
22.(8分)(2020春 覃塘区期末)如图,D,E,G分别是AB,AC,BC边上的点,∠1+∠2=180°,∠3=∠B.
(1)请说明DE∥BC的理由;
(2)若DE平分∠ADC,∠2=2∠B,判断CD与EG的位置关系,并说明理由.
23.(8分)(2010春 吉安期末)如图,在△ABC和△DEF中,∠B=∠E=90°,BC=a,AC=b,EF=m,DF=n,且a、b、m、n满足下列条件:(a﹣m)2+|b﹣n|=0.
(1)△ABC和△DEF全等吗?请说明理由;
(2)AB∥DE吗?为什么?
24.(2019春 黄浦区期中)(1)如图1,已知直线m∥n,在直线n上取A、B两点,C、P为直线m上的两点,无论点C、P移动到任何位置都有:S△ABC S△ABP(填“>”、“<”或“=”)
(2)如图2,在一块梯形田地上分别要种植大豆(空白部分)和芝麻(阴影部分),若想把种植大豆的两块地改为一块地,且使分别种植两种植物的面积不变,请问应该怎么改进呢?写出设计方案,并在图中画出相应图形并简述理由.
(3)如图3,王爷爷和李爷爷两家田地形成了四边形DEFG,中间有条分界小路(图中折线ABC),左边区域为王爷爷的,右边区域为李爷爷的.现在准备把两家田地之间的小路改为直路,请你用有关的几何知识,按要求设计出修路方案,并在图中画出相应的图形,说明方案设计理由.(不计分界小路与直路的占地面积).
2021-2022学年下学期上海初中数学七年级期末典型试卷2
参考答案与试题解析
一.选择题(共6小题,满分18分,每小题3分)
1.(3分)(2021秋 韶关期末)已知三角形的两边长分别为4和9,则下列数据中,能作为第三边长的是( )
A.2 B.3 C.4 D.9
【考点】三角形三边关系.
【专题】三角形;推理能力.
【分析】首先根据三角形的三边关系定理,求得第三边的取值范围,再进一步找到符合条件的数值.
【解答】解:设这个三角形的第三边为x.
根据三角形的三边关系定理,得:9﹣4<x<9+4,
解得5<x<13.
故选:D.
【点评】本题考查了三角形的三边关系定理.掌握构成三角形的条件:两边之和>第三边,两边之差<第三边是解决问题的关键.
2.(3分)(2021春 温江区校级期中)下列运算正确的是( )
A.(2m﹣3)(﹣2m+3)=﹣4m2﹣9 B.(2m+1)(2m﹣1)=2m2﹣1
C.(﹣2m﹣1)2=4m2+4m+1 D.(2m+3)2=4m2+6m+9
【考点】平方差公式;完全平方公式.
【专题】整式;运算能力.
【分析】根据平方差公式、完全平方公式结构特征进行判断即可.
【解答】解:A.(2m﹣3)(﹣2m+3)=﹣4m2+12m﹣9,因此选项A不符合题意;
B.(2m+1)(2m﹣1)=4m2﹣1,因此选项B不符合题意;
C.(﹣2m﹣1)2=4m2+4m+1,因此选项C符合题意;
D.(2m+3)2=4m2+12m+9,因此选项D不符合题意;
故选:C.
【点评】本题考查平方差公式、完全平方公式,掌握完全平方公式、平方差公式的结构特征是正确解答的前提.
3.(3分)下列各数中,最小的是( )
A. B. C. D.
【考点】分数指数幂;实数大小比较.
【专题】计算题.
【分析】根据分数指数幂的运算即可求出答案.
【解答】解:(A)()6=23=8,
(B)原式=()6=32=9,
(C)原式=()623=8,
(D)原式=()6=6,
故选:D.
【点评】本题考查分数指数幂,解题的关键是熟练运用分数指数幂的运算,本题属于基础题型.
4.(3分)下列说法正确的是( )
A.有两边及一边的对角分别相等的两个三角形全等
B.有两边相等的两个直角三角形全等
C.有两个角及第三个角的对边分别相等的两个三角形全等
D.有两个角及一边相等的两个三角形全等
【考点】直角三角形全等的判定;等腰三角形的性质;勾股定理;全等三角形的判定.
【专题】图形的全等;推理能力.
【分析】根据全等三角形的判定判断即可.
【解答】解:A、有两边及一边的对角分别相等的两个三角形不一定全等,说法错误,不符合题意;
B、有两边相等的两个直角三角形不一定全等,说法错误,不符合题意;
C、有两个角及第三个角的对边分别相等的两个三角形全等,说法正确,符合题意;
D、有两个角及一边相等的两个三角形不一定全等,说法错误,不符合题意;
故选:C.
【点评】本题考查了全等三角形的判定定理的理解,能熟练地运用判定定理进行推理是解此题的关键.
5.(3分)(2021春 静安区校级期末)如图,直线a、b被直线c所截,下列说法正确的是( )
A.当a∥b时,一定有∠1=∠2
B.当∠1=∠2时,一定有a∥b
C.当a∥b时,一定有∠1+∠2=90°
D.当∠1+∠2=180°时,一定有a∥b
【考点】平行线的判定与性质.
【专题】线段、角、相交线与平行线;推理能力.
【分析】根据平行线的判定定理即性质定理求解判断即可.
【解答】解:如图,
A、当a∥b时,∠1=∠3,
∵∠2+∠3=180°,
∴∠2+∠1=180°,
故A错误,不符合题意;
B、当∠1=∠2时,且∠1=∠2=90°,才有a∥b,
故B错误,不符合题意;
C、当a∥b时,∠1=∠3,
∵∠3+∠2=180°,
∴∠1+∠2=180°,
故C错误,不符合题意;
D、当∠1+∠2=180°时,
∵∠3+∠2=180°,
∴∠1=∠3,
∴一定有a∥b,
故D正确,符合题意;
故选:D.
【点评】此题考查了平行线的判定与性质,熟练掌握平行线的判定定理与性质定理是解题的关键.
6.(3分)(2021秋 射洪市期中)已知,则的算术平方根是( )
A. B. C.±2 D.2
【考点】二次根式有意义的条件.
【专题】二次根式;运算能力.
【分析】根据二次根式有意义的条件求出b,进而求出a,根据算术平方根的概念计算即可.
【解答】解:由题意得:b﹣8≥0,8﹣b≥0,
解得:b=8,
则a=2,
∴4,
∵4的算术平方根是2,
∴的算术平方根是2,
故选:D.
【点评】本题考查的是二次根式有意义的条件,算术平方根,掌握二次根式的被开方数是非负数是解题的关键.
二.填空题(共11小题,满分18分)
7.(3分)(2021春 普陀区期中)2021年1月份国家统计局发布数据显示,初步核算,2020年全年国内生产总值(GDP)为1015986亿元.请将数字“1015986”保留3个有效数字并用科学记数法表示为 1.02×106 .
【考点】科学记数法与有效数字.
【专题】计算题;实数;运算能力.
【分析】用科学记数法保留有效数字,要在标准形式a×10n中a的部分保留,从左边第一个不为0的数字数起,需要保留几位就数几位,然后根据四舍五入的原理进行取舍.
【解答】解:1015986=1.015986×106≈1.02×106.
故答案是:1.02×106.
【点评】本题主要考查了科学记数法以及有效数字,从左边第一个不是0的数开始数起,到精确到的数位为止,所有的数字都叫做这个数的有效数字;注意后面的单位不算入有效数字.
8.(3分)(2020 雁塔区校级模拟)已知实数(3)0,,,0.101001,,,其中为无理数的是 , .
【考点】无理数;零指数幂;算术平方根;立方根.
【专题】实数;数感.
【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此进行解答即可.
【解答】解:(3)0=1,是整数,属于有理数;
0.101001是有限小数,属于有理数;
是分数,属于有理数;
,是整数,属于有理数;
无理数有:,.
故答案为:,.
【点评】此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.
9.(3分)(2021春 静安区校级期末)在数轴上,点A、点B对应的数分别是和,则AB= 3 .
【考点】实数与数轴.
【分析】本题依据绝对值的实际意义,任意两点间的距离等于这两个点所代表的数差的绝对值即得到答案.
【解答】解:∵点A、点B对应的数分别是和,∴.
故答案为:.
【点评】本题主要考查了数轴上两点之间距离的求法,关键需要灵活应用绝对值得实际意义.
10.(3分)(2021 西城区校级开学)6 3 .
【考点】二次根式的混合运算.
【专题】二次根式;运算能力.
【分析】直接化简二次根式,再利用二次根式的乘法运算法则化简,进而合并同类二次根式得出答案.
【解答】解:原式6
=22
=3.
故答案为:3.
【点评】此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.
11.(2021春 闵行区校级期中)比较大小: > .
【考点】实数大小比较.
【分析】分别计算出()2和()2的值,比较和的大小,变形即可得到答案.
【解答】解:∵()2=28+2,
()2=28+2,
∴),
∴.
故答案为:>.
【点评】本题考查的是实数的大小比较,掌握完全平方公式、正确进行不等式的变形是解题的关键.
12.(3分)(2020秋 铜官区期末)已知:2x+3y+3=0,计算:4x 8y的值= .
【考点】幂的乘方与积的乘方;同底数幂的乘法.
【专题】计算题;整式;数感;运算能力.
【分析】根据幂的乘方与积的乘方、同底数幂的乘法的计算公式即可得结果.
【解答】解:∵2x+3y+3=0,
∴2x+3y=﹣3,
4x 8y=22x 23y=2(2x+3y)=2﹣3.
故答案为:.
【点评】本题考查了幂的乘方与积的乘方、同底数幂的乘法,解决本题的关键是掌握幂的乘方与积的乘方、同底数幂的乘法.
13.(2021春 嘉定区期末)在△ABC中,如果∠A:∠B:∠C=3:4:5,那么∠A= 45° .
【考点】三角形内角和定理.
【专题】三角形;推理能力.
【分析】根据三个角的比可设设∠A=3x,∠B=4x,∠C=5x,再利用三角形的内角和定理列方程,解方程可求解x值,即可求解∠A的度数.
【解答】解:设∠A=3x,∠B=4x,∠C=5x,
∵∠A+∠B+∠C=180°,
∴3x+4x+5x=180°,
解得x=15°,
∴∠A=3x=45°,
故答案为:45°.
【点评】本题主要考查三角形的内角和定理,运用方程思想解决问题是解题的关键.
14.(2021春 嘉定区期末)如果将点M(m,3)向左平移2个单位到达点N,这时点N恰好在y轴上,那么m的值是 2 .
【考点】坐标与图形变化﹣平移.
【专题】平面直角坐标系;平移、旋转与对称;符号意识.
【分析】根据向右平移横坐标加,向上平移纵坐标加即可得解.
【解答】解:将点M(m,3)向左平移2个单位到达点N,这时点N恰好在y轴上,
∴m﹣2=0,
∴m=2.
故答案为:2.
【点评】本题考查了坐标与图形变化﹣平移,熟记平移中点的变化规律:横坐标右移加,左移减;纵坐标上移加,下移减是解题的关键.
15.(2021春 嘉定区期末)如图,AD∥CE,△ACD的面积为a,那么△EAD的面积为 a .
【考点】三角形的面积;平行线之间的距离.
【专题】三角形;推理能力.
【分析】利用平行线之间的距离处处相等得到C点和E点到AD的距离相等,然后利用三角形面积公式求解.
【解答】解:∵AD∥CE,
∴C点和E点到AD的距离相等,
∴S△EAD=S△CAD=a.
故答案为:a.
【点评】本题考查了三角形的面积:三角形的面积等于底边长与高线乘积的一半,即S△底×高.也考查了平行线之间的距离.
16.(2019春 连云港期末)如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.如图2,若∠MPN=75°,且射线PQ绕点P从PN位置开始,以每秒15°的速度逆时针旋转,射线PM同时绕点P以每秒5°的速度逆时针旋转,当PQ与PN成180°时,PQ与PM同时停止旋转,设旋转的时间为t秒.当射线PQ是∠MPN的“巧分线”时,t的值为 3或或 .
【考点】角的计算.
【专题】分类讨论;线段、角、相交线与平行线.
【分析】分3种情况,根据巧分线定义得到方程求解即可.
【解答】解:当∠NPQ∠MPN时,
15t(75+5t),
解得t=3;
当∠NPQ∠MPN时,
15t(75+5t),
解得t.
当∠NPQ∠MPN时,
15t(75+5t),
解得t.
故t的值为3或或.
故答案为:3或或.
【点评】本题考查了旋转的性质,巧分线定义,学生的阅读理解能力及知识的迁移能力.理解“巧分线”的定义是解题的关键.
17.(3分)(2019春 丰城市期末)将一副三角板按如图放置,小明得到下列结论:①如果∠2=30°,则有AC∥DE;②∠BAE+∠CAD=180°;③如果BC∥AD,则有∠2=30°;④如果∠CAD=150°,则∠4=∠C;那么其中正确的结论有 ①②④ .
【考点】平行线的判定与性质.
【专题】线段、角、相交线与平行线;三角形.
【分析】根据平行线的性质和判定和三角形内角和定理逐个判断即可.
【解答】解:∵∠2=30°,∠CAB=90°,
∴∠1=60°,
∵∠E=60°,
∴∠1=∠E,
∴AC∥DE,故①正确;
∵∠CAB=∠DAE=90°,
∴∠BAE+∠CAD=90°﹣∠1+90°+∠1=180°,故②正确;
∵BC∥AD,∠B=45°,
∴∠3=∠B=45°,
∵∠2+∠3=∠DAE=90°,
∴∠2=45°,故③错误;
∵∠CAD=150°,∠BAE+∠CAD=180°,
∴∠BAE=30°,
∵∠E=60°,
∴∠BOE=∠BAE+∠E=90°,
∴∠4+∠B=90°,
∵∠B=45°,
∴∠4=45°,
∵∠C=45°,
∴∠4=∠C,故④正确;
故答案为:①②④.
【点评】本题考查了三角形的内角和定理和平行线的性质和判定,能灵活运用定理进行推理是解此题的关键.
三.解答题(共7小题,满分46分)
18.(2021春 嘉定区期末)计算:(2)2﹣(1).
【考点】二次根式的混合运算.
【专题】二次根式;运算能力.
【分析】先利用完全平方公式、二次根式的乘法法则和二次根式的性质计算,然后合并即可.
【解答】解:原式=3﹣44﹣3
=3﹣44﹣34
=﹣3.
【点评】本题考查了二次根式的混合运算:熟练掌握二次根式的性质、二次根式的乘法法则是解决问题的关键.
19.(12分)(2018春 静安区期中)()0+(28)﹣()﹣2
【考点】实数的运算;分数指数幂;零指数幂;负整数指数幂.
【专题】计算题.
【分析】首先计算乘方、乘法,然后从左向右依次计算,求出算式的值是多少即可.
【解答】解:()0+(28)﹣()﹣2
=1+4﹣9
=﹣4
【点评】此题主要考查了实数的运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.
20.(10分)(2021春 静安区校级期末)已知BC=4,根据下列条件,画图及填空:
(1)画△ABC,使∠B=30°,∠C=60°.
(2)在(1)的条件下,画△ABC的中线BD.
(3)在(1)、(2)的条件下,从∠A引出一条射线,将△ABC切割成两个等腰三角形,射线与边BC相交于点E,请画出射线AE,在图中标出∠CAE的大小,并写出CD= 1 .
【考点】作图—复杂作图;线段垂直平分线的性质;等腰三角形的性质.
【专题】作图题;几何直观;应用意识.
【分析】(1)如图1所示,将量角器中心与点B对齐,0刻度线与BC对齐,内圈30°线条指向作射线BP;将量角器中心与点C对齐,0刻度线与BC对齐,外圈60°线条指向作射线CQ;射线BP与CQ交点为点A,则△ABC即为所求.
(2)如图2所示,取AC中点为点D,作线段BD,则BD为△ABC的中线,线段BD即为所求.
(3)在△ABC内部作∠CAE=∠C=60°,射线AE即为所求.
【解答】解:(1)如图1中,△ABC即为所求;
(2)如图2中,线段BD即为所求;
(3)如图3所示,射线AE即为所求.
∵∠ABC=30°,∠C=60°,
∴∠BAC=90°,
∴ACBC=2,
∴CD=AD=1,
故答案为:1.
【点评】本题考查作图﹣复杂作图,等腰三角形的性质,直角三角形30度角的性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
21.(8分)(2021春 虹口区校级期末)∠1与∠2互补,∠2比∠1的3倍的大20°,求∠1、∠2的大小.
【考点】余角和补角.
【专题】线段、角、相交线与平行线;推理能力.
【分析】直接利用补角的定义结合∠2比∠1的3倍的大20°,得出等式求出答案.
【解答】解:由题意得,
则有∠1+3∠1+20°=180°,4∠1=160°,∠1=40°,
则∠2=3∠1+20°=3×40°+20°=140°,
∴∠1=40°;∠2=140°.
【点评】本题考查了余角和补角,掌握余角和补角的性质是解题的关键.
22.(8分)(2020春 覃塘区期末)如图,D,E,G分别是AB,AC,BC边上的点,∠1+∠2=180°,∠3=∠B.
(1)请说明DE∥BC的理由;
(2)若DE平分∠ADC,∠2=2∠B,判断CD与EG的位置关系,并说明理由.
【考点】平行线的判定与性质.
【专题】线段、角、相交线与平行线;推理能力.
【分析】(1)根据已知条件和对顶角相等可证明AB∥EG,再根据平行线的性质得角相等,再等量代换可得∠3=∠EGC,进而可得DE∥BC;
(2)根据已知条件可得∠B=45°,可以证明CD⊥AB,再由AB∥EG,即可得CD⊥EG.
【解答】解:(1)∵∠1+∠2=180°,∠1=∠DFG,
∴∠1+∠DFG=180°,
∴AB∥EG,
∴∠B=∠EGC,
又∵∠B=∠3,
∴∠3=∠EGC,
∴DE∥BC;
(2)CD⊥EG.
理由如下:
∵DE平分∠ADC,
∴∠ADE=∠EDC,
∵DE∥BC,
∴∠B=∠ADE=∠EDC,
又∵∠2=2∠B,∠2+∠ADE+∠EDC=180°,
∴2∠B+∠B+∠B=180°,
∴∠B=45°,
∴∠2=2∠B=90°,
∴CD⊥AB
又∵AB∥EG,
∴CD⊥EG.
【点评】本题考查了平行线的判定与性质,解决本题的关键是区别平行线的判定与性质并熟练运用.
23.(8分)(2010春 吉安期末)如图,在△ABC和△DEF中,∠B=∠E=90°,BC=a,AC=b,EF=m,DF=n,且a、b、m、n满足下列条件:(a﹣m)2+|b﹣n|=0.
(1)△ABC和△DEF全等吗?请说明理由;
(2)AB∥DE吗?为什么?
【考点】全等三角形的判定与性质;非负数的性质:绝对值;非负数的性质:偶次方;平行线的判定.
【专题】证明题;探究型.
【分析】(1)首先解等式根据非负数性质,可判断a=m,b=n;则BC=EF,AC=DF;由∠B=∠E=90°,易得△ABC≌△DEF.
(2)利用第(1)问的全等可得到∠A=∠D,所以AB∥DE(内错角相等,两直线平行).
【解答】解:(1)△ABC≌△DEF;
理由:(a﹣m)2+|b﹣n|=0,
∵(a﹣m)2≥0,|b﹣n|≥0,
∴a﹣m=0,b﹣n=0,a=m,b=n;
∵BC=a,AC=b,EF=m,DF=n,
∴BC=EF,AC=DF;
在Rt△ABC和Rt△DEF中,
AC=DF,BC=EF,
∴Rt△ABC≌Rt△DEF(HL);
(2)AB∥DE;
理由:∵△ABC≌△DEF(已证),
∴∠A=∠D(全等三角形对应角相等),
∴AB∥DE(内错角相等,两直线平行).
【点评】本题考查了全等三角形的判定和性质;题目通过解等式考查了非负数的性质,而且得到了线段之间相等的关系,从而能判三角形全等;由三角形全等得到角相等,又确定了两直线的平行关系;考法新颖,是一道考查学生综合能力的好题.
24.(2019春 黄浦区期中)(1)如图1,已知直线m∥n,在直线n上取A、B两点,C、P为直线m上的两点,无论点C、P移动到任何位置都有:S△ABC = S△ABP(填“>”、“<”或“=”)
(2)如图2,在一块梯形田地上分别要种植大豆(空白部分)和芝麻(阴影部分),若想把种植大豆的两块地改为一块地,且使分别种植两种植物的面积不变,请问应该怎么改进呢?写出设计方案,并在图中画出相应图形并简述理由.
(3)如图3,王爷爷和李爷爷两家田地形成了四边形DEFG,中间有条分界小路(图中折线ABC),左边区域为王爷爷的,右边区域为李爷爷的.现在准备把两家田地之间的小路改为直路,请你用有关的几何知识,按要求设计出修路方案,并在图中画出相应的图形,说明方案设计理由.(不计分界小路与直路的占地面积).
【考点】作图—应用与设计作图;平行线之间的距离;三角形的面积;梯形.
【专题】作图题;几何直观;运算能力;推理能力.
【分析】(1)根据等底等高的三角形面积相等即可得结论;
(2)根据同底等高的三角形面积相等即可设计改进方案;
(3)根据同底等高的三角形面积相等即可设计修路方案.
【解答】解:(1)∵m∥n,
∴△ABC与△ABP等底等高,
∴S△ABC=S△ABP.
故答案为:=;
(2)方法一:
连接AC,将△ACD的区域用于种植大豆,
△ABC的区域用于种植芝麻,
理由:由于同底等高,
所以S△ACE=S△ABE,
所以S△ABE+S△ECD=S△ACE+S△ECD,
即S△ACD=S△ABE+S△ECD,
同理S△ACB=S△BCE,
方法二
连接BD,将△ABD的区域用于种植大豆,
△BCD的区域用于种植芝麻,
理由:由于同底等高,
所以S△BED=S△ECD,
所以S△ABE+S△ECD=S△ABE+S△BED,
即S△ABD=S△ABE+S△ECD,
同理S△BCD=S△BCE.
(3)方法一
连接AC,过B点作AC的平行线PQ,
连接AQ,AQ即为所修直路.
将四边形ADEQ的区域分给王爷爷,
四边形AGFQ的区域分给李爷爷,
理由:由于同底等高,
所以S△BCQ=S△ABQ,
所以S△ABP+S△BCQ=S△ABP+S△ABQ,
即S△APQ=S△ABP+S△BCQ,
同理S△ABC=S△ACQ.
方法二:
连接AC,过B点作AC的平行线PQ,
连接PC,PC即为所修直路.
将四边形CEDP的区域分给王爷爷,
四边形CPGF的区域分给李爷爷,
理由:由于同底等高,
所以S△ABP=S△PBC,
所以S△ABP+S△BCQ=S△PBC+S△BCQ.
即S△CPQ=S△APB+S△BCQ.
同理S△ABC=S△ACP.
【点评】本题考查了作图﹣应用与设计作图,解决本题的关键是掌握等底等高的两个三角形的面积相等
第1页(共1页)
同课章节目录
