北师大版八年级数学上册第二章1《认识无理数》教案(第1课时)
文档属性
| 名称 | 北师大版八年级数学上册第二章1《认识无理数》教案(第1课时) |

|
|
| 格式 | doc | ||
| 文件大小 | 75.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-14 20:21:25 | ||
图片预览

文档简介
第二章 实数
《认识无理数》教案(第1课时)
教学目标:
(1)通过拼图活动,让学生感受客观世界中非有理数的存在,培养学生的动手操作能力和求知探索精神;
(2)能判断线段的长度是否为非有理数,加深对有理数和非有理数的理解.
教学重点:寻找生活中的非有理数
教学难点:能判断某些线段的长度是否为非有理数
一、教学过程设计
本节课设计了7个教学环节:
第一环节:复习回顾,引入课题; 第二环节:合作探究;
第三环节:课堂练习; 第四环节:小故事展示环节;
第五环节:当堂检测: 第六环节:课堂小结;
第七环节:作业布置.
第一环节:复习回顾
数的产生过程。
第二环节:合作探究
合作探究一:
把两个边长为1的小正方形通过剪、拼,设法得到一个大正方形,你会吗?
【议一议】: 已知,请问:①可能是整数吗?②可能是分数吗?
合作探究二:
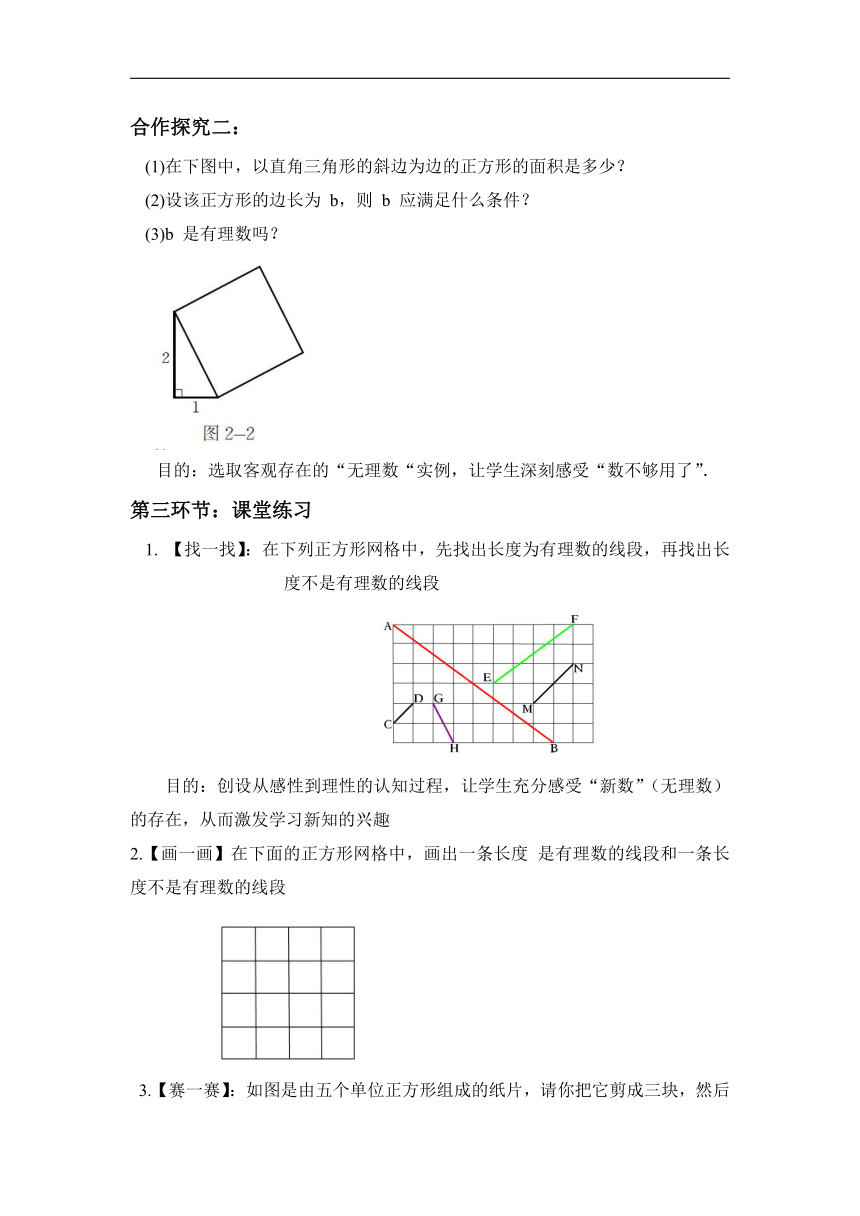
(1)在下图中,以直角三角形的斜边为边的正方形的面积是多少?
(2)设该正方形的边长为 b,则 b 应满足什么条件?
(3)b 是有理数吗?
目的:选取客观存在的“无理数“实例,让学生深刻感受“数不够用了”.
第三环节:课堂练习
1. 【找一找】:在下列正方形网格中,先找出长度为有理数的线段,再找出长度不是有理数的线段
目的:创设从感性到理性的认知过程,让学生充分感受“新数”(无理数)的存在,从而激发学习新知的兴趣
2.【画一画】在下面的正方形网格中,画出一条长度 是有理数的线段和一条长度不是有理数的线段
3.【赛一赛】:如图是由五个单位正方形组成的纸片,请你把它剪成三块,然后拼成一个正方形,你会吗?试试看!
第四环节:展示环节:分享无理数小故事
第五环节:当堂检测
1.下列各数中,是有理数的是( )
A.面积为 3 的正方形的边长 B.体积是 8 的正方体的棱长
C.两直角边长分别为 2 和 3 的直角三角形的斜边长 D.圆周率π
2.正方形网格中,每个小正方形的边长为 1,则网格上的三角形
ABC 中,边长为无理数的有( )
A.0 条 B.1 条 C.2 条 D.3 条
第六环节:课堂小结
1.通过本节课的学习,感受到有理数又不够用了, 请问你有什么收获与体会?
2.客观世界中,的确存在不是有理数的数,你能列举几个吗?
3.除了本课所认识的非有理数的数以外,你还能找到吗?
目的:引导学生自己小结本节课的知识要点及数学方法,使知识系统化.
第七环节:布置作业
1.完成《学案》今日作业部分
2.预习下节课,完成《学案》相关内容
3.选作作业:画一个三角形使其三边都为非无理数。
教学设计反思
(一)生活是数学的源泉,兴趣是学习的动力
大量事实都证明一点,与生活贴得越近的东西最容易引起学习者的浓厚兴趣,才能激发学习者的学习积极性,学习才可能是主动的.本节课中教师首先用拼图游戏引发学生学习的欲望,把课程内容通过学生的生活经验呈现出来,然后进行大胆置疑,生活中的数并不都是有理数,那它们究竟是什么数呢?从而引发了学生的好奇心,为获取新知,创设了积极的氛围.在教学中,不要盲目的抢时间,让学生能够充分的思考与操作.
(二)化抽象为具体
常言道:“数学是锻炼思维的体操”,数学教师应通过一系列数学活动开启学生的思维,因此对新数的学习不能仅仅停留于感性认识,还应要求学生充分理解,并能用恰当数学语言进行解释.正是基于这个原因,在教学过程中,刻意安排了一些环节,加深对新数的理解,充分感受新数的客观存在,让学生觉得新数并不抽象.
(三)强化知识间联系,注意纠错
既然称之为“新数”,那它当然不是有理数,亦即不是整数,也不是分数,所以“新数”不可以用分数来表示,这为进一步学习“新数”,即第二课时教学埋下了伏笔,在教学中,要着重强调这一点:“新数”不能表示成分数,为无理数的教学奠好基.
献身科学,执着追求
第一个发现这样的数的人却被抛进大海,你想知道这其中的曲折离奇吗?这得追溯到2500年前,有个叫毕达哥拉斯的人,他是一个伟大的数学家,他创立了毕达哥拉斯学派,这是一个非常神秘的学派,他们以领袖毕达哥拉斯为核心,认为毕达哥拉斯是至高无尚的,他所说的一切都是真理。
毕达哥拉斯( Pythagoras) 认为“宇宙间的一切现象都能归结为整数或整数之比,即都可用有理数来描述。
但后来,这学派的一位年轻成员希伯索斯(Hippasus) 发现边长为1的正方形的对角线的长不能用有理数来表示,这就动摇了毕达哥拉斯学派的信条,引起了信徒们的恐慌,他们试图封锁这一发现,然而希伯索斯偷偷将这一发现传播出去,这为他招来了杀身之祸,在他逃回家的路上,遭到毕氏成员的围捕,被投入大海。
他这一死,使得这类数的计算推迟了500多年,给数学的发展造成了不可弥补的损失。
《认识无理数》教案(第1课时)
教学目标:
(1)通过拼图活动,让学生感受客观世界中非有理数的存在,培养学生的动手操作能力和求知探索精神;
(2)能判断线段的长度是否为非有理数,加深对有理数和非有理数的理解.
教学重点:寻找生活中的非有理数
教学难点:能判断某些线段的长度是否为非有理数
一、教学过程设计
本节课设计了7个教学环节:
第一环节:复习回顾,引入课题; 第二环节:合作探究;
第三环节:课堂练习; 第四环节:小故事展示环节;
第五环节:当堂检测: 第六环节:课堂小结;
第七环节:作业布置.
第一环节:复习回顾
数的产生过程。
第二环节:合作探究
合作探究一:
把两个边长为1的小正方形通过剪、拼,设法得到一个大正方形,你会吗?
【议一议】: 已知,请问:①可能是整数吗?②可能是分数吗?
合作探究二:
(1)在下图中,以直角三角形的斜边为边的正方形的面积是多少?
(2)设该正方形的边长为 b,则 b 应满足什么条件?
(3)b 是有理数吗?
目的:选取客观存在的“无理数“实例,让学生深刻感受“数不够用了”.
第三环节:课堂练习
1. 【找一找】:在下列正方形网格中,先找出长度为有理数的线段,再找出长度不是有理数的线段
目的:创设从感性到理性的认知过程,让学生充分感受“新数”(无理数)的存在,从而激发学习新知的兴趣
2.【画一画】在下面的正方形网格中,画出一条长度 是有理数的线段和一条长度不是有理数的线段
3.【赛一赛】:如图是由五个单位正方形组成的纸片,请你把它剪成三块,然后拼成一个正方形,你会吗?试试看!
第四环节:展示环节:分享无理数小故事
第五环节:当堂检测
1.下列各数中,是有理数的是( )
A.面积为 3 的正方形的边长 B.体积是 8 的正方体的棱长
C.两直角边长分别为 2 和 3 的直角三角形的斜边长 D.圆周率π
2.正方形网格中,每个小正方形的边长为 1,则网格上的三角形
ABC 中,边长为无理数的有( )
A.0 条 B.1 条 C.2 条 D.3 条
第六环节:课堂小结
1.通过本节课的学习,感受到有理数又不够用了, 请问你有什么收获与体会?
2.客观世界中,的确存在不是有理数的数,你能列举几个吗?
3.除了本课所认识的非有理数的数以外,你还能找到吗?
目的:引导学生自己小结本节课的知识要点及数学方法,使知识系统化.
第七环节:布置作业
1.完成《学案》今日作业部分
2.预习下节课,完成《学案》相关内容
3.选作作业:画一个三角形使其三边都为非无理数。
教学设计反思
(一)生活是数学的源泉,兴趣是学习的动力
大量事实都证明一点,与生活贴得越近的东西最容易引起学习者的浓厚兴趣,才能激发学习者的学习积极性,学习才可能是主动的.本节课中教师首先用拼图游戏引发学生学习的欲望,把课程内容通过学生的生活经验呈现出来,然后进行大胆置疑,生活中的数并不都是有理数,那它们究竟是什么数呢?从而引发了学生的好奇心,为获取新知,创设了积极的氛围.在教学中,不要盲目的抢时间,让学生能够充分的思考与操作.
(二)化抽象为具体
常言道:“数学是锻炼思维的体操”,数学教师应通过一系列数学活动开启学生的思维,因此对新数的学习不能仅仅停留于感性认识,还应要求学生充分理解,并能用恰当数学语言进行解释.正是基于这个原因,在教学过程中,刻意安排了一些环节,加深对新数的理解,充分感受新数的客观存在,让学生觉得新数并不抽象.
(三)强化知识间联系,注意纠错
既然称之为“新数”,那它当然不是有理数,亦即不是整数,也不是分数,所以“新数”不可以用分数来表示,这为进一步学习“新数”,即第二课时教学埋下了伏笔,在教学中,要着重强调这一点:“新数”不能表示成分数,为无理数的教学奠好基.
献身科学,执着追求
第一个发现这样的数的人却被抛进大海,你想知道这其中的曲折离奇吗?这得追溯到2500年前,有个叫毕达哥拉斯的人,他是一个伟大的数学家,他创立了毕达哥拉斯学派,这是一个非常神秘的学派,他们以领袖毕达哥拉斯为核心,认为毕达哥拉斯是至高无尚的,他所说的一切都是真理。
毕达哥拉斯( Pythagoras) 认为“宇宙间的一切现象都能归结为整数或整数之比,即都可用有理数来描述。
但后来,这学派的一位年轻成员希伯索斯(Hippasus) 发现边长为1的正方形的对角线的长不能用有理数来表示,这就动摇了毕达哥拉斯学派的信条,引起了信徒们的恐慌,他们试图封锁这一发现,然而希伯索斯偷偷将这一发现传播出去,这为他招来了杀身之祸,在他逃回家的路上,遭到毕氏成员的围捕,被投入大海。
他这一死,使得这类数的计算推迟了500多年,给数学的发展造成了不可弥补的损失。
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
